What Does to Evaluate Mean in Math?

When students first encounter the instruction to evaluate in mathematics, it can seem like just another confusing term in an already complex subject. However, understanding what it means to evaluate is fundamental to mathematical success. 

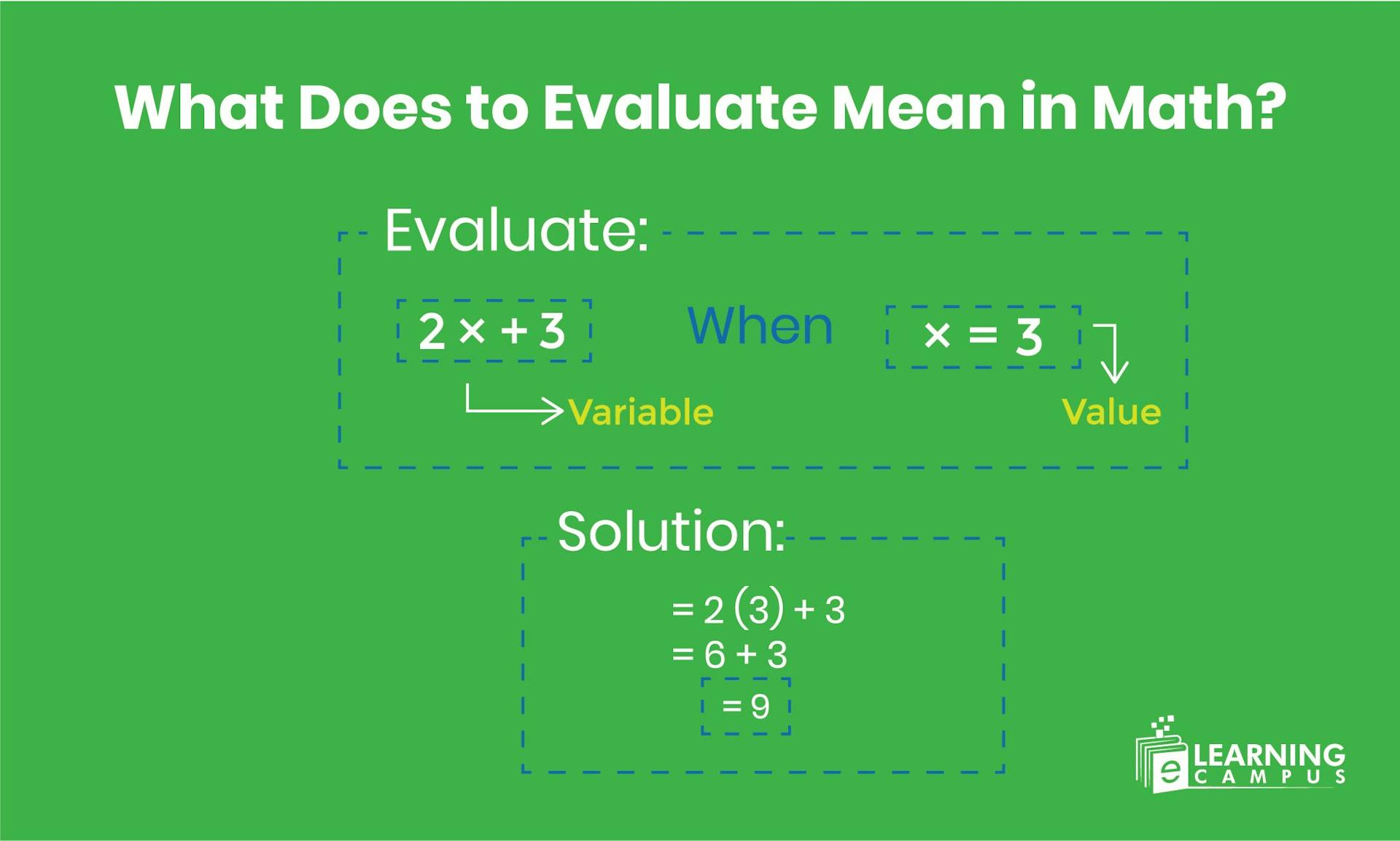
In mathematics, to evaluate means to calculate the numerical value of an expression.

This blog will explore the meaning, applications, and various interpretations of evaluation in mathematics.

What does Evaluate Mean in Math

To evaluate in mathematics means to find the numerical value of an expression or equation. When we evaluate something, we calculate its worth or determine its specific value under given conditions. 

For example, solving a mathematical puzzle where you replace variables with specific numbers and perform the necessary operations to arrive at a single answer.

The process of evaluation involves substitution, simplification, and calculation. 

Understanding Mathematical Expressions and Their Evaluation

A mathematical expression is a combination of numbers, variables, and operations that represents a value. When you are asked to evaluate an expression, you need to perform all the indicated operations in the correct order to find the final answer.

For example, if you are asked to evaluate the expression 3 + 4 × 2, 

you would follow the order of operations (PEMDAS/BODMAS) to get 3 + 8 = 11. The evaluation process requires careful attention to mathematical rules and conventions to ensure accuracy.

Evaluating Expressions with Variables

One of the most common applications of evaluation involves expressions containing variables. Variables are letters or symbols that represent unknown or changing values. When we evaluate an expression with variables, we substitute specific values for those variables and then calculate the result.

Example 

Consider the expression 5x + 3. 

To evaluate this expression when x = 4, we would substitute 4 for x. 

5(4) + 3 = 20 + 3 = 23. 

This process of substitution and calculation is at the heart of algebraic evaluation.

Evaluation allows us to see how expressions behave with different input values. By evaluating the same expression with various substitutions, we can understand patterns, relationships, and mathematical behavior.

Evaluating Algebraic Expressions

An algebraic expression contains variables (like x, y, z) along with numbers and operations. To evaluate an algebraic expression, we substitute given values for the variables and then calculate the result using PEMDAS.

Basic Steps to Evaluate Algebraic Expressions

• Substitute the given values for the variables
• Follow PEMDAS to perform operations in the correct order
• Calculate to find the final numerical answer

Evaluating Single Variable

Evaluate 3x + 7 when x = 5

Solution:

• Substitute x = 5 
• 3(5) + 7
• Multiply: 15 + 7
• Add: 22

Answer: 22

Evaluating Expression with Exponents

Evaluate: 2x² - 5 when x = 4

Solution:

• Substitute x = 4: 2(4)² - 5
• Exponent first: 2(16) - 5
• Multiply: 32 - 5
• Subtract: 27

Answer: 27

Evaluating Expression with Multiple Variables

Evaluate: 3a + 2b - 4 when a = 6 and b = 3

Solution:

• Substitute a = 6 and b = 3: 3(6) + 2(3) - 4
• Multiply: 18 + 6 - 4
• Add and subtract (left to right): 24 - 4 = 20

Answer: 20

Evaluating Complex Expression

Evaluate: 4x² + 3xy - y when x = 2 and y = 5

Solution:

• Substitute x = 2 and y = 5: 4(2)² + 3(2)(5) - 5
• Exponents: 4(4) + 3(2)(5) - 5
• Multiply (left to right): 16 + 30 - 5
• Add and subtract: 46 - 5 = 41

Answer: 41

The Order of Operations in Evaluation

The correct evaluation of expressions depends on following the correct order of operations. This hierarchy ensures that everyone evaluates expressions consistently and arrives at the same correct answer. The standard order is:

• Parentheses (or other grouping symbols)
• Exponents and roots
• Multiplication and division (from left to right)
• Addition and subtraction (from left to right)

When evaluating complex expressions, carefully working through each step according to this order prevents common mistakes and ensures accurate results. 

Evaluating Expressions by PEMDAS

Evaluating expressions with PEMDAS (Parentheses, Exponents, Multiplication & Division, Addition & Subtraction) means following a specific order of operations to solve math problems consistently, tackling grouping symbols first, then powers, then multiplication/division (left-to-right), and finally addition/subtraction (left-to-right) to get the correct result. 

Example 

Evaluate the expression 3 + 4 × 2² - (8 ÷ 4) + 5

Step-by-Step Solution

Step 1: Parentheses first

• Solve (8 ÷ 4) = 2
• Expression becomes: 3 + 4 × 2² - 2 + 5

Step 2: Exponents

• Solve 2² = 4
• Expression becomes: 3 + 4 × 4 - 2 + 5

Step 3: Multiplication and Division (left to right)

• Solve 4 × 4 = 16
• Expression becomes: 3 + 16 - 2 + 5

Step 4: Addition and Subtraction (left to right)

• 3 + 16 = 19
• 19 - 2 = 17
• 17 + 5 = 22

Answer: 22

Evaluating Functions: A Higher Level of Mathematics

Function evaluation is a more sophisticated application of the evaluation concept. A function is a special relationship where each input produces exactly one output.

Example 

A function looks like f(x) = 2x² - 5x + 1,

 To evaluate f(3), we substitute 3 for every x in the function.

f(3) = 2(3)² - 5(3) + 1 

2(9) - 15 + 1

18 - 15 + 1 = 4

Function evaluation is crucial in advanced mathematics, science, and real-world applications. It allows us to model situations, make predictions, and understand relationships between quantities.

Get expert online Math Tutor for effective learning

Practical Applications of Mathematical Evaluation

Understanding evaluation extends far beyond the classroom. In everyday life, we constantly evaluate mathematical expressions, often without realizing it. When calculating tips at restaurants, determining sale prices, or measuring ingredients for recipes, we're performing evaluation.

In professional contexts, evaluation becomes even more critical. Engineers evaluate formulas to design structures, economists evaluate models to predict market trends, and scientists evaluate equations to understand natural phenomena. The ability to accurately evaluate mathematical expressions is a foundational skill that supports countless practical applications.

Common Variations in Evaluation Terminology

The mathematical community sometimes uses different terms that essentially mean the same thing as evaluate. You might encounter instructions like "calculate," "compute," "find the value of," or "solve for" in various contexts. While these terms have subtle distinctions, they generally direct you to perform similar evaluation processes.

Understanding these variations in terminology helps students navigate different textbooks, instructors, and mathematical contexts. Recognizing that these terms often point to the same fundamental process, determining numerical values, reduces confusion and builds mathematical confidence.

Help your kids learn Math online in a safe and secure environment. 

Strategies for Accurate Evaluation in Math

Becoming proficient at evaluation requires practice and attention to detail. Here are some strategies to improve your evaluation skills:

• Start by clearly identifying what you are being asked to evaluate. 
• Read the problem carefully and note any given values for variables. 
• Write out each step of your work rather than trying to do everything mentally. 

This systematic approach helps catch errors and makes your reasoning transparent.

• Double-check your substitutions to ensure you've replaced variables correctly. 
• Pay special attention to negative numbers, which are common sources of error. 
• When substituting a negative value, use parentheses to maintain clarity: if x = -3 and you are evaluating x², write (-3)² rather than -3².

Always verify your final answer makes sense in context. If you're evaluating an expression that represents a physical quantity, consider whether your answer is reasonable.

Evaluation in Different Mathematical Contexts

The concept of evaluation appears throughout mathematics in various forms. In geometry, you might evaluate formulas for area, volume, or perimeter using specific measurements. In trigonometry, you evaluate trigonometric functions at particular angles. In calculus, you evaluate limits, derivatives, and integrals.

Each mathematical domain has its own evaluation conventions and techniques, but the underlying principle remains constant: determine the specific value under given conditions.

Conclusion

Evaluation in Math is the process of finding specific numerical results. By learning the techniques of substitution, following the order of operations, and practicing systematic calculation, you can develop confidence and competence in mathematical evaluation. This fundamental skill serves as a building block for more advanced mathematical concepts and real-world applications, making it well worth the effort to understand thoroughly.