Math Variable Problems

Have you ever felt confused in your exam while solving Math variable problems? Students are usually tricked by such types of problems. Math problems with variables are easy to solve once you get the method to solve them. 

In this blog, you will learn everything from basic one-variable equations to complex multi-variable systems. We will provide you with the Math variable problems with solutions. 

What is a variable in a math problem? 

A variable is a symbol, typically a letter like x, y, or z, that represents an unknown value or a quantity that can change. Variables are the foundation of algebra and appear in countless mathematical applications, from simple equations to complex scientific formulas.

Here are some math variable equation examples. 

In these examples, x, y, and z are variables whose values are unknown. With the help of the given equation, we can find their values. 

Get expert online math tutoring for enduring learning.  

How to Solve Math Problems with Variables

The math problems may have several variables. Some equations have single variables, some have two or three variables. The method for solving problems depends on the number of variables present in the equation. 

How to Solve Single Variable Problems

Single variable problems are those equations in which only one variable is needed to solve. When solving math problems with variables, follow these systematic steps:

• Identify what the variable represents: Read the problem carefully and define your variable
• Set up the equation: Translate words into mathematical symbols
• Isolate the variable: Use inverse operations to get the variable alone
• Solve and verify: Calculate the answer and check it in the original equation

Example:  Solve the equation

Add 10 to both sides

Example 2: A number increased by 8 equals 20. Find the number.

Let x = the unknown number

Equation:

Subtract 8 from both sides

How to Solve a Math Problem with 2 Variables

To solve a math problem with two variables, find the values for both unknowns simultaneously. Math problems with two variables typically require two equations to solve completely.

There are two methods to solve the math problems with 2 variables.

1. Substitution Method
2. Elimination Method

Substitution Method

The substitution method is an algebraic technique to solve a system of linear equations by substituting the expression of one variable from one equation into the other equation. This reduces the system to a single equation with one variable, which can then be solved. 

Steps for the Substitution Method (for a system of two linear equations) 

• Isolate one variable: Choose one of the equations and solve for one of the variables (either x or y) in terms of the other variable. This step is easiest when a variable has a coefficient of 1 or -1.
• Substitute the expression: Substitute the expression for the isolated variable into the other equation. This creates a new equation with only one variable.
• Solve the new equation: Solve the resulting single-variable equation using standard arithmetic and algebraic operations.
• Back-substitute: Substitute the numerical value you found in Step 3 back into the equation from Step 1 (or any of the original equations) to solve for the other variable.
• Verify the solution: Check the solution (an ordered pair) by plugging both values into both of the original equations to ensure they are true.

Example: Solve the system: x + y = 10 and 2x - y = 5

x + y = 10…….equation 1

2x - y = 5……..equation 2

Solve Eq. 1 for x

x = 10 - y…… equation 3

Substitute the value of x in Eq. 2

Substitute the value of y in Eq. 3

The solution is (5, 5)

Elimination Method

The elimination method is a technique for solving a system of two or more linear equations by adding or subtracting the equations to eliminate one variable. 

Steps of solving problems by the elimination method 

• Multiply equations to create opposite coefficients
• Add or subtract equations to eliminate one variable
• Solve for the remaining variable
• Substitute back to find the other variable

Example: Solve: 3x + 2y = 16 and 5x - 2y = 8.

In equations I and II,  the y coefficients are opposites. We don’t need to multiply it.

Add the equations

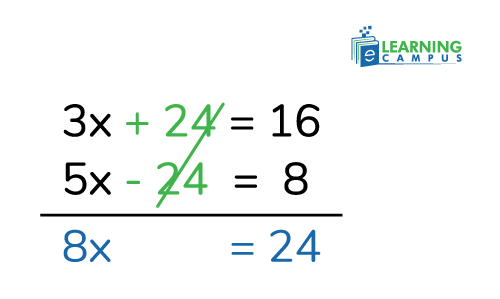
The answer is

Simplify this equation by dividing both sides by -5, then 

Now, eliminate z from Equations 2 and 3

Multiply equation 2 by 2 to get +2z, then add it to equation 3.

Now add the two equations

The answer is

The simplified equation is

Now we have two equations of 2 Variables

x + y = 1 (from new equation 1) 

x + 4y = -2 (from new equation 3)

It is now much easier to solve the two-variable equations. 

We will solve the equations for x and y 

Subtract the first equation from the second

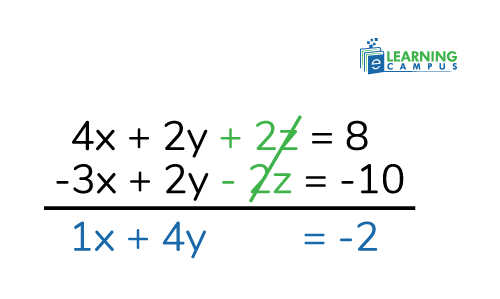
The answer is

Simplify this equation

Substitute the value of y into x + y = 1

Find z using the original equation 2

Now put x = 2 and y = -1 back into equation 2

The final solution is:

How to Solve Math Problems with Variables on Both Sides

To solve the math problems with variables on both sides, get all variable terms on one side of the equation. Then solve the equation accordingly. 

Steps for solving

• Move all variable terms to one side (typically the left)
• Move all constant terms to the other side
• Simplify and solve

Example: Solve

This equation has a variable on both sides. 

Subtract 2x from both sides

Subtract 3 from both sides

Divide both sides by 3

x = 5

Independent and Dependent Variables in Math Word Problems

Independent and dependent variables in math word problems highlight the cause-and-effect relationships. The independent variable is the value you control or change. The dependent variable is the value that responds to changes in the independent variable.

Examples of independent and dependent variables in math word problems:

1. Temperature and ice cream sales: If we track ice cream sales at different temperatures, temperature is the independent variable (what changes naturally), and sales are the dependent variable (what responds to temperature).
2. Study time and test scores: Hours studied are the independent variable (what the student controls), and the test score is the dependent variable (the result of studying).
3. Price and demand: When a store changes prices to see how it affects sales, price is independent, and quantity sold is dependent.

Math Problems with Variables Worksheets

Math variable problems worksheets are practice materials for finding the unknown value (the variable) in an algebraic equation or expression. 

These worksheets teach students to write equations from word problems, simplify expressions by combining like terms, and solve for the variable by isolating it through operations like addition, subtraction, multiplication, and division. 

You can download the variable math problems worksheets in PDF below. 

Also, get the adding and subtracting integers worksheet

Download the worksheet

Conclusion 

Math variable problems form the foundation of algebraic thinking and problem-solving. From understanding what a variable is in a math problem to tackling the hardest math problems that contain variables, you explored a comprehensive overview of concepts and techniques.