elearning BlogPolynomial Expressions | Types and Simplification

Polynomial Expressions | Types and Simplification

Polynomial expressions and it's types 

Polynomials are basic and interesting concepts in Mathematics. Understanding the polynomial expressions is important to know and solve the complex algebraic equations. 

In this blog, you will learn about polynomials, their types, polynomial in standard form, and how to simplify polynomials in detail with examples. 

What are Polynomials

The word polynomial can be broken into two terms, ‘poly’ which means many and ‘nominal’ which means term. So, the polynomial can be defined as a Mathematical expression that contains more terms. 

As per the definition, polynomials contain variables, constants, exponents, and arithmetic operations that represent the relation between two or more variables. 

We will understand it through examples.

For example:

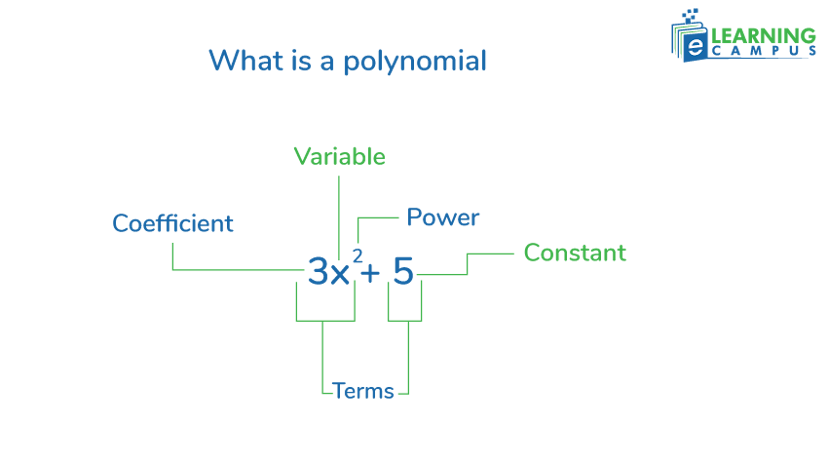
Look at this polynomial

2x2+62x^2 + 6
  • The coefficient is a number attached to any variable in an algebraic expression. In the above polynomial, the first term is 2x2 in which 2 is the coefficient. 
  • The variable is an unknown term in an expression that can change and is represented by alphabets. In the above example, the term is x known as the variable. 
  • The exponent is the power of a variable. The power of x in the above polynomial is the exponent which is 2.
  • The constant is any digit that is fixed and appears alone in an expression. The constant in the above example is 6. 

These terms have been highlighted in the image below.

Terms of polynomial expression

Standard Form of Polynomial Expressions

In the standard form of polynomial expression, the terms are written in descending order of exponent or degree of a variable. The polynomial standard form is expressed as;

P(x)=anxn+an−1xn−1+…+a2x2+a1x+a0P(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_2 x^2 + a_1 x + a_0
Where  an,  an−1,  a1,  a0  are coefficients.Where \; a_n, \; a_{n-1}, \; a_1, \; a_0 \; \text{are coefficients.}
andxn,xn−1,x2,xare variables.\text{and} \quad x^n, \quad x^{n-1}, \quad x^2, \quad x \quad \text{are variables.}

Degree of a Polynomial

In polynomials, the highest exponent of the term is known as the Degree of a Polynomial. The calculation of polynomial degree for a Single Variable Polynomial is different from Multivariable Polynomial. 

Let’s learn how to find a polynomial degree in detail.

Degree of a Single Variable Polynomial 

A single-variable polynomial contains only one variable in each term. For example,

3x3+2x2+x+43x^3 + 2x^2 + x + 4

In this polynomial, there is only one variable x in each term.

To find the degree of polynomial with a single variable, follow the following steps.

  1. Write the like terms combined. 
  2. Rewrite polynomials in standard form. 
  3. Choose the highest exponent of the term, it is the degree of a single-variable polynomial. 

Example: 

In this single-variable polynomial,

3x3 + 2x2 + x + 43x^3 \,+\, 2x^2 \,+\, x \,+\, 4

the degree of the polynomial is 3 because it is the highest exponent in the polynomial. 

Degree of Multivariable Polynomial  

The multivariable polynomials have two or more variables in terms. For example,

4x3y2 + 1x2y + 3y + 64x^3y^2 \,+\, 1x^2y \,+\, 3y \,+\, 6

In this polynomial, two different variables x and y appear. 

To find the degree of the multivariable polynomials, follow these steps.

  1. Combine the like terms. 
  2. Write the standard form of polynomials. 
  3. Add the exponent of the variables.
  4. Choose the highest exponent. 

Example:  

Find the degree of the term of polynomial

4x3y2z+1x2y2+3yz+64x^3y^2z + 1x^2y^2 + 3yz + 6

To calculate this polynomial expression degree, we will add the exponents of each term and choose the highest value as the degree. 

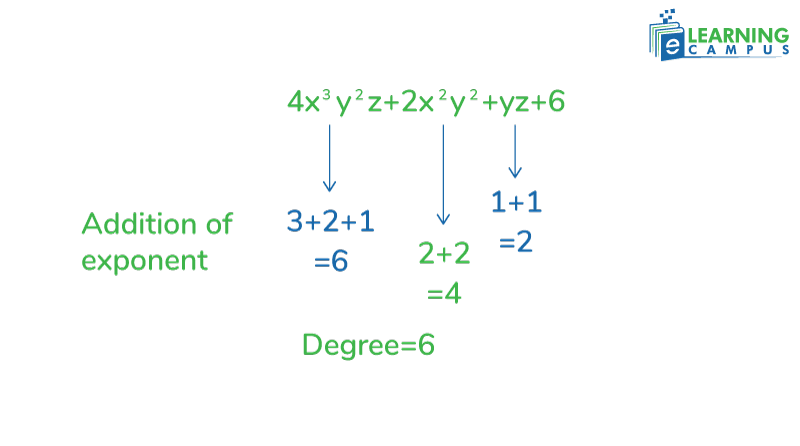
degree of a polynomial with example

Types of Polynomial

Polynomials are divided into different categories based on the degree and number of terms present in a polynomial. There are three types of polynomials based on the terms and four types based on degree.

Let’s understand each type by classifying polynomials by degree and number of terms in detail with the examples. 

Classifying Polynomials by Number of Terms

We get three categories by classifying polynomials by number of terms present in the expression. They are: Monomial, Binomial, and Trinomial. 

Monomial 

A polynomial with one term is known as a Monomial. The condition for a monomial is that the term should be non-zero. For example,

2x,  5x2,  6x3y22x, \; 5x^2, \; 6x^3y^2

in the example,

2x,  5x2,  and  6x3y2 are single terms.2x, \; 5x^2, \; \text{and} \; 6x^3y^2 \quad \text{ are single terms.}

Binomial

A polynomial with two terms is called a Binomial. It is written by a combination of two monomials with a positive or negative sign in between. For example,

3x2 + 4y3  and  7x3 − 3xy23x^2 \,+\, 4y^3 \; \textbf{and} \; 7x^3 \,-\, 3xy^2

Each of these polynomials has two terms. 

Trinomial 

A polynomial with three terms is named a trinomial. For example,

6x3y2 + 2x2 + 3  and  x3 + 5xy3 − 76x^3y^2 \,+\, 2x^2 \,+\, 3 \; \textbf{and} \; x^3 \,+\, 5xy^3 \,-\, 7

Classification of Polynomial by Degree 

Polynomials are also classified based on the degree. There are four types of polynomials based on the degree of polynomials. Let’s learn polynomial names by degree with examples.

Linear Polynomial 

A linear polynomial is a polynomial whose degree is always equal to one. The linear polynomial example is x + y - 5, the highest degree of term is 1. 

Quadratic Polynomial

A polynomial with the highest degree of two is called Quadratic Polynomial. For example,

6x3−xy+x2−46x^3 - xy + x^2 - 4

The highest degree of both the polynomials is 2. 

Cubic Polynomial 

The polynomial whose degree is three is known as a cubic polynomial. For example,

6x3 − xy + x2 − 46x^3 \,-\, xy \,+\, x^2 \,-\, 4

Zero Polynomial 

A polynomial whose leading coefficient and degree of polynomial is zero is known as the zero polynomial. 

Simplifying Polynomial Expressions

Simplifying Polynomial expressions refers to the process of making complex expressions simple either by addition, subtraction, or multiplication. You will learn how to simplify a polynomial using different methods.

Simplifying Polynomial by Combining Like Terms 

Combining the like terms is a method of Simplifying Polynomials. In this method, the terms with the same variable and exponents are combined, and arithmetic operation is applied. It involves the following steps;

  1. Combine the like terms, i.e., having the same variable and exponent.
  2. Write the terms in descending order of exponents.
  3. Add the coefficient of terms.
  4. Keep the exponent the same.

Example:

Simplify this polynomial

5x5 + 2x2 − 4x3 + 3 − 8x3 − 3x5 + 2 − x5x^5 \,+\, 2x^2 \,-\, 4x^3 \,+\, 3 \,-\, 8x^3 \,-\, 3x^5 \,+\, 2 \,-\, x
  • First, we will combine the like terms with the descending order of exponent. 
5x5 − 3x5 − 4x3 − 8x3 + 2x2 − x2 + 3 + 25x^5 \,-\, 3x^5 \,-\, 4x^3 \,-\, 8x^3 \,+\, 2x^2 \,-\, x^2 \,+\, 3 \,+\, 2
  • Now, apply the arithmetic operation accordingly. 
2x5 − 12x3 + x2 + 52x^5 \,-\, 12x^3 \,+\, x^2 \,+\, 5
  • So, in simplification we get
2x5−12x3+x2+52x^5 - 12x^3 + x^2 + 5

Enjoy Math With Online Tutor  

Are you in search of an expert online math tutor to make math fun for your kids? We can help you. We have a professional team of math teachers to make math easy for your kids.

Hire maths tutor online
Hire a Tutor Now

FAQs