Is Zero a Real Number? Everything You Need to Know

Have you ever thought which group of numbers zero belongs to? Students usually get confused about “Is zero a real number?” It's one of those questions that seems simple on the surface but can actually trip up a lot of students. The short answer is, yes, zero is absolutely a real number. 

But there is a lot more to understand about why that is true and what it means in different mathematical contexts. In this blog, we will break down everything you need to know about zero and its place in the number system, answering all those confusing questions about it. 

Is Zero a Real Number?

Yes, zero is definitely a real number. In mathematics, real numbers include all the numbers you can find on the number line, such as positive numbers, negative numbers, fractions, and decimals. And zero sits right there in the middle. Zero is the number that separates positive numbers from negative numbers, and it plays an important role in our number system.

Understanding Real Numbers

Real numbers are basically any numbers that represent a quantity or position on a continuous line. This includes; 

• Whole numbers, like 1, 2, 3,
• Integers, which add negative numbers like -1, -2, -3
• Rational numbers, such as fractions like 1/2 or 3/4
• Irrational numbers (like π or √2). 

Zero fits perfectly into this system as both a whole number and an integer, which automatically makes it a real number.

Why Zero is Classified as a Real Number

Zero is classified as a real number because it meets all the criteria for being a real number. 

• It can be placed on the number line. 
• It can be used in arithmetic operations (with some exceptions).
• It represents a concrete mathematical concept, the absence of quantity. 

Just because zero represents ‘nothing’ does not mean it is not a real number. In fact, zero is one of the most important numbers in mathematics.

Is Zero a Positive Real Number?

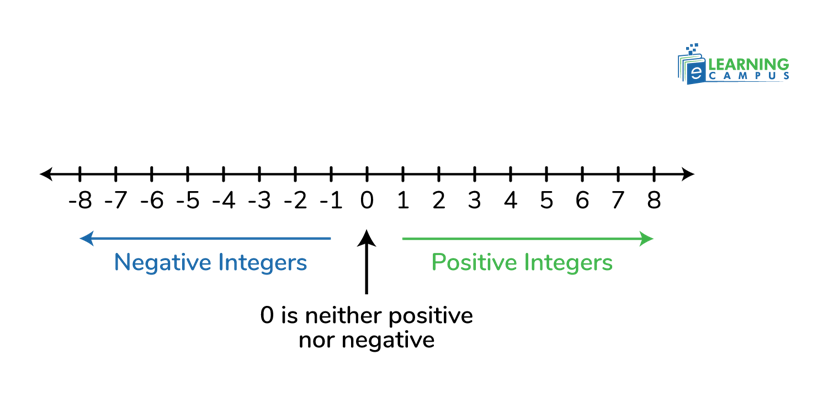
No, zero is not a positive real number. This is a common source of confusion. Positive numbers are greater than zero, and since zero equals itself, it can't be greater than itself. Think of it this way: positive numbers are on the right side of zero on the number line, and zero is the dividing point, not part of either side.

The Distinction Between Positive and Non-Negative

While zero is not positive, it is considered "non-negative." Non-negative numbers include zero and all positive numbers. So when we say "non-negative," it means zero or greater. This distinction matters in many mathematical contexts, especially in algebra and calculus.

Is Zero a Positive or Negative Real Number?

Zero is neither a positive nor a negative real number. It is the neutral point between positive and negative numbers. Some people get confused because they think everything has to be one or the other, but zero is special. It is the only real number that is neither positive nor negative. It is the origin point, the reference from which we measure everything else.

Is Zero a Non-Negative Real Number?

Yes, zero is a non-negative real number. In Mathematics, non-negative numbers include both positive numbers and zero itself. This terminology is commonly used in mathematics when you want to exclude negative numbers but include zero.

• The concept of non-negative numbers is particularly important in contexts where negative values don't make sense. 
• For example, we can't have a negative distance or a negative probability. 
• In these cases, we use non-negative real numbers, which means zero and all positive numbers. There can be zero distance or zero probability. 

Is Zero a Real Number in Math and Algebra?

Yes, zero is a fundamental real number in all branches of mathematics, including algebra. In fact, zero plays some special roles in algebra that make it particularly important.

Zero in Algebraic Operations

In algebra, zero has unique properties. 

• When we add zero to any number, we get that number back. This is called the additive identity. For example, 

5+0=5

50+0=50

• When we multiply any number by zero, we get zero. For example,

150×0=0

1000×0=1000

These properties make zero essential for solving equations and understanding mathematical relationships.

Is Zero a Real Number in Algebra?

Yes, zero is also a real number in algebra. It is used constantly in algebraic equations, and understanding zero's properties is crucial for solving problems. For instance, when we solve equations like x² - 4 = 0, we're looking for values of x that make the equation equal to zero.

Is Negative Zero a Real Number?

Zero can not be negative. In standard mathematics, there is no concept of "negative zero". Zero is zero, and it does not have a sign. However, in computer science and floating-point arithmetic, negative zero can exist as a technical representation, but mathematically speaking, -0 = 0. They are the same number.

The Concept of Signed Zero

When a sign, negative or positive, is associated with zero, it is called a signed zero. In everyday math, we do not distinguish between +0 and -0. They are identical. 

−0 = +0 = 0

The idea of signed zeros only appears in specialized computing contexts. But for all practical mathematical purposes, zero has no sign. It is neither positive nor negative.

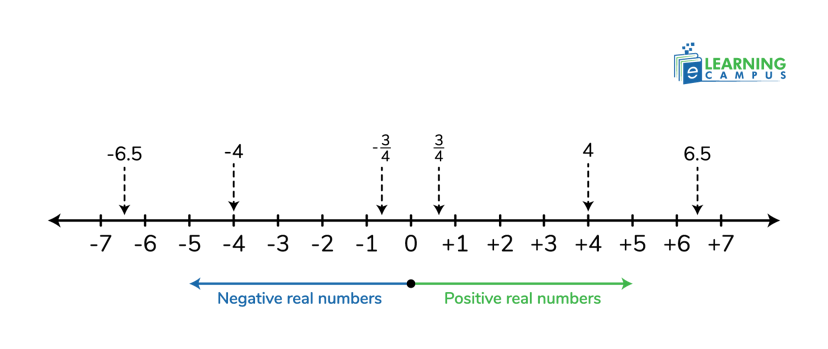
Is Zero a Negative Real Number?

No, zero is not a negative real number. Negative numbers are less than zero, and zero can't be less than itself. Negative real numbers are all the numbers to the left of zero on the number line, and zero marks the boundary, not part of the negative portion.

Is the Square Root of Zero a Real Number?

Yes, the square root of zero is a real number, and it equals zero. This makes sense when you think about it: what number, when multiplied by itself, gives you zero? The answer is zero (because 0 × 0 = 0). So,

√0 = 0

Since zero is a real number, the square root of zero is also a real number. It is one of the few numbers whose square root is itself, along with one.

√1 = 1

Is Zero a Real or Imaginary Number?

Zero is a real number, but it is also technically an imaginary number. In fact, zero is the only number that's both real and imaginary. Let me explain.

Understanding Imaginary Numbers

Imaginary numbers are multiples of the imaginary unit ‘i’ (where i = √-1). So imaginary numbers look like 0i, 1i, 2i, 3i, etc. 

Now, 0i = 0, which means zero can be written as an imaginary number. 

But since zero is also on the real number line, it belongs to both sets. However, in most contexts, we simply call zero a real number because that's its primary classification.

What is a Non-Zero Real Number?

A non-zero real number is simply any real number except zero. This includes all positive numbers (1, 2, 3.5, π, etc.) and all negative numbers (-1, -2, -0.5, etc.). The term "non-zero" is used when we want to exclude zero from consideration, which happens often in mathematics.

Why We Distinguish Non-Zero Numbers

We make this distinction because zero behaves differently in certain operations. Most importantly, we cannot divide by zero. So when we are talking about division or certain algebraic operations, we specifically say "non-zero real numbers" to make it clear that zero is not included.

Every Real Number is a Zero of the Zero Polynomial

This is a special case in algebra. The zero polynomial is the polynomial where all coefficients are zero, so it looks like f(x) = 0. No matter what value of x you plug in, you always get zero. Therefore, every real number is a zero of the zero polynomial because every number makes it equal to zero.

Why This Matters

This might seem like a trivial observation, but it's actually important in polynomial theory. The zero polynomial is unique because it has infinitely many zeros (every real number), whereas most polynomials have a limited number of zeros based on their degree.

Is a Number Divided by Zero a Real Number?

No, division by zero is undefined. It does not produce a real number or any number at all. This is one of the fundamental rules in mathematics. You cannot divide by zero because it breaks the logical consistency of arithmetic.

Why Division by Zero Doesn't Work

Think about what division means: 

if we say 6 ÷ 2 = 3, we are asking "what number times 2 gives us 6?" 

Now, if we try to calculate 6 ÷ 0, we're asking "what number times 0 gives us 6?" But any number times zero equals zero, not six. There is no answer that works. So, division by zero is undefined.

Is Zero a Whole Real Number?

Yes, zero is a whole number. Whole numbers are the counting numbers plus zero: 0, 1, 2, 3, 4, and so on. Since all whole numbers are also real numbers, zero is both a whole number and a real number.

The Number Hierarchy

Here's how zero fits into the number system hierarchy:

• Zero is a whole number
• Zero is an integer (integers include whole numbers and their negatives)
• Zero is a rational number (it can be written as 0/1)
• Zero is a real number (rational numbers are a subset of real numbers)

Conclusion 

Zero (0) is a real number. It belongs to the set of all numbers on the number line, encompassing whole numbers, integers, rationals, and irrationals. It acts as the crucial additive identity (0 + b = b), a rational number, and can be seen within the complex numbers as 0 + 0i. All these properties make it a fundamental part of the real number system.