Integers- Types, Operations, and Properties

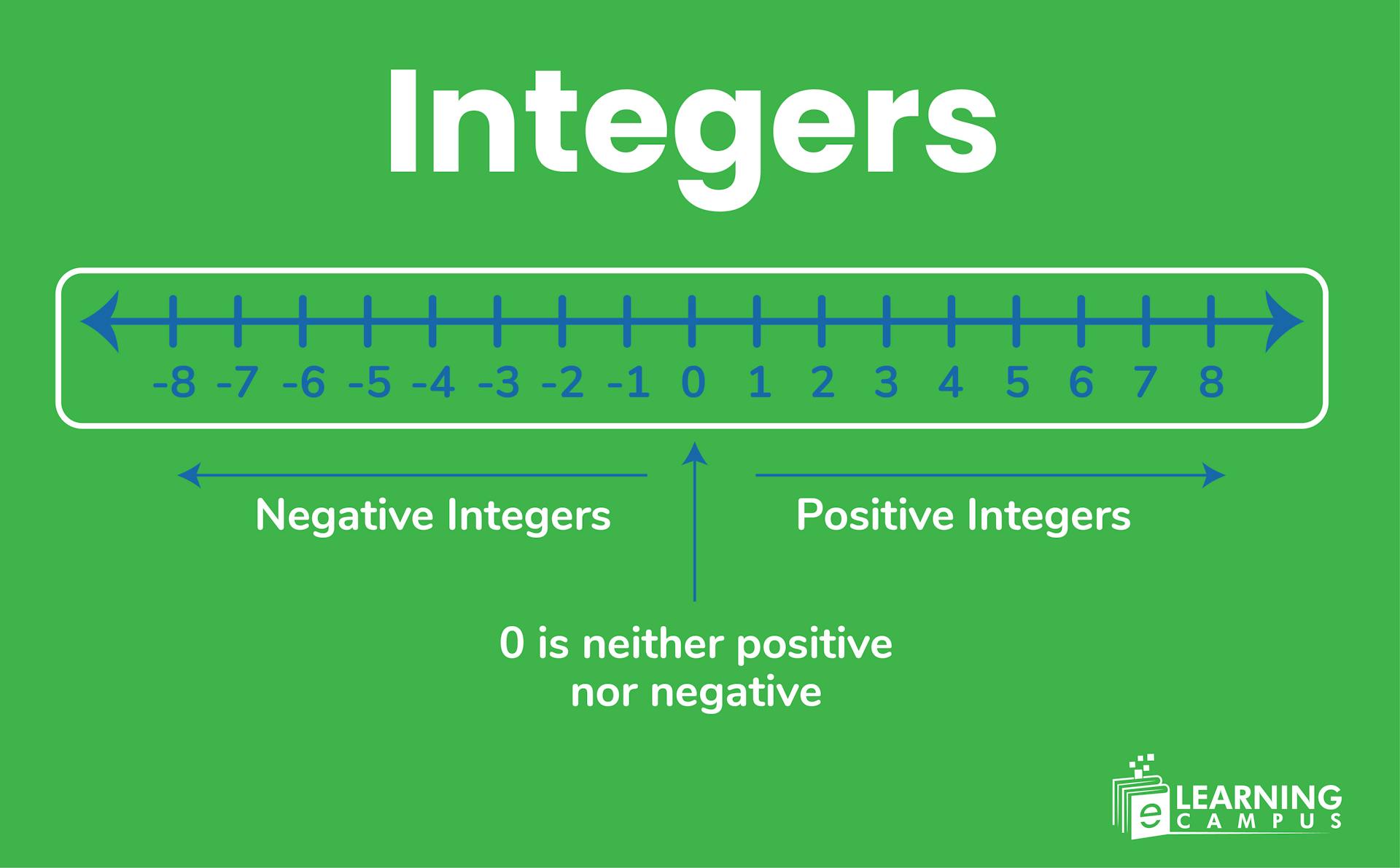
Integers are the numbers that do not possess a fractional part. An integer can be a negative number, a positive number, or zero. Every integer is a rational number. Any number that contains a fraction or decimal cannot be an integer. All the arithmetic operations, such as addition, subtraction, multiplication, and division, can be performed on integers. 

What are Integers 

Integer is a Latin word that means ‘whole’ or ‘intact’. So, all those numbers that are not fractions or decimals are known as integers. All whole numbers are integers. The whole numbers include 0 and all natural numbers. 

Types of Integers 

Integers are broadly classified into three types, which include positive integers, negative integers, and zero.

•  Positive integers are the numbers that are greater than zero. For example, 1, 2, 3,.....
•  Negative integers are the numbers that are less than zero. The negative integers are written with a negative sign. For example, -1, -2, -3, -4 . . . . 
•  Zero is a whole number. It is neither a negative number nor a positive number. 

Representation of Integers 

In mathematics, the set of numbers is represented by a specific symbol. The set of integers is represented by ‘Z’. The set is represented as;

Z = {... -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, ...}

Arithmetic Operations on Integers

The four operations in Mathematics i.e, addition, subtraction, multiplication, and division are known as the arithmetic operations. These mathematical operations can be performed on the integers. 

Let’s look at how arithmetic operations are performed on the integers. 

Addition of Integers 

The addition of integers is to sum up two or more integers. The value of the sum of integers may vary depending on the integer in use. There are several rules related to the use of integers in addition. 

Integer Rules for Adding

The following integer rules for adding should be kept in mind while performing arithmetic operations.  

• While adding integers with the same sign, the numbers will simply be added, and the same sign will be assigned to the answer. 
• While adding integers with different signs, i.e, one negative and one positive, the numbers will be subtracted and the sign of the larger number will be assigned to the answer. For example, -5+3=-2

Subtraction of Integers 

In the subtraction of integers, we find the difference between two or more integers. The value of the difference might vary depending on the integers used in the operation. An integer subtracted from an integer is an integer.

Subtraction Rule of Integers 

While performing subtraction on the integers, the following rules are followed;

• Change the sign of the subtrahend (the second number that is being subtracted). 
• Then follow the rule used for the addition of integers.

For example, -7-3

          Change the sign of the second number 

           (-7) – (+3)

             (-7) +3

Multiplication of Integers 

The multiplication of an integer is the process of finding the product of two or more integers. An integer multiplied by an integer is an integer. The multiplication of integers is carried out by simply multiplying the numbers. 

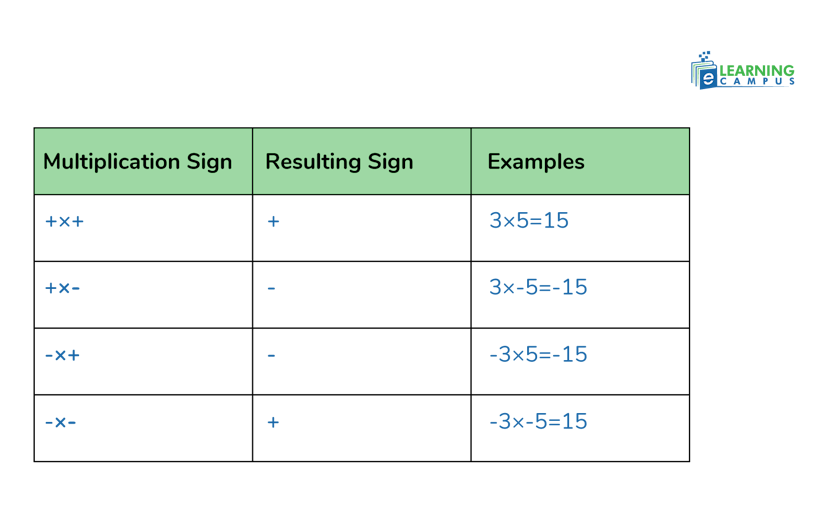
Multiplication Rules of Integers

The multiplication of integers always follows these basic rules.

• If both the integers have the same sign( negative or positive), then the result will always be positive.
• If the integers have different signs (one positive and one negative), then the result will always be negative.

For example, 

           (+2) x (+4) = +8

            (+3) x (-5) = – 15

The multiplication of the integer rules chart below summarizes the rule of signs while performing multiplication.

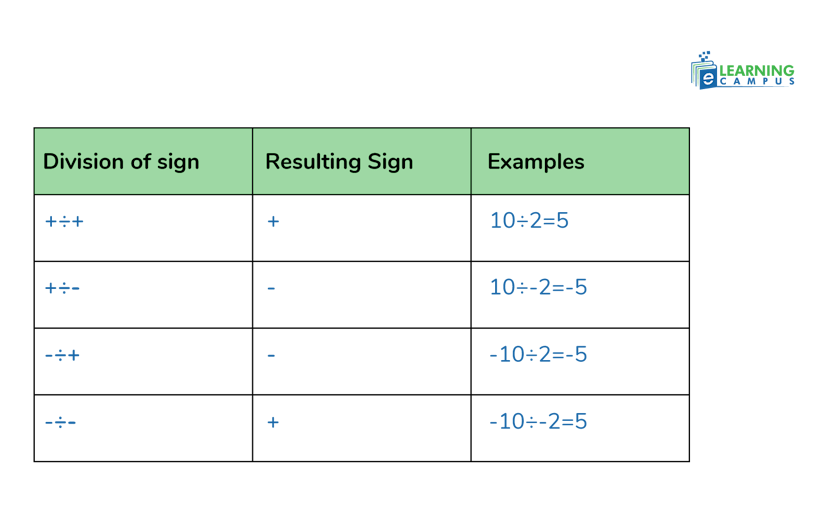
Division of Integers 

Division can also be performed on the integers. The rules of dividing any integer is the same as the multiplication of integers. 

• If both the integers have the same sign( negative or positive), then the result will always be positive.
• If the integers have different signs (one positive and one negative), then the result will always be negative.

The division of integer rules anchor chart is displayed below.

Integers in a Number Line

A number line is a horizontal straight line used to represent the numbers visually. The positive and negative integers on a number line are represented with ‘0’ at the centre. Positive integers are written to the right of zero, while negative integers are written to the left of zero.

Adding Integers on a Number Line

Integers can be added by using the number line. It can be done by taking the second number into account. While adding integers on a number line, we usually follow these simple rules.

• We always begin from "0".
• We will move to the right side of the ‘0’ if the number is positive.
• We will move to the left side of the ‘0’ if the number is negative

Let’s look at the addition of integers examples on the number line.

Example: Solve 6 + (-10) using a number line. 

To solve the problem with the help of a number line, we will consider the rules.

• The first number, 6, is positive, so we will move six steps right from ‘0’.

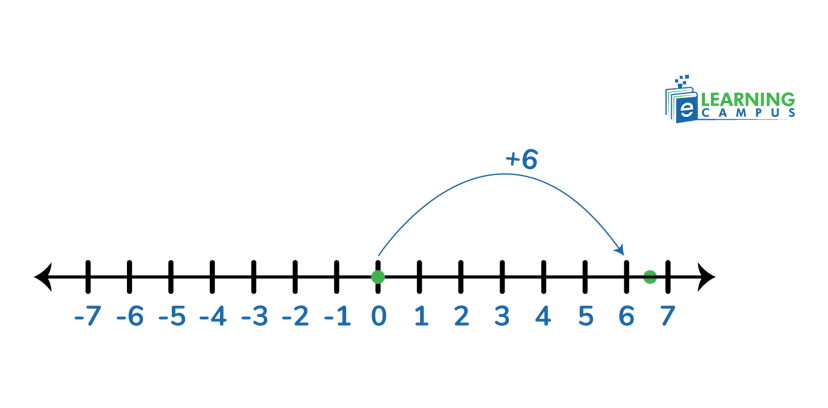
• The second number ‘10’ is negative, so we will move 10 steps left from ‘6’.

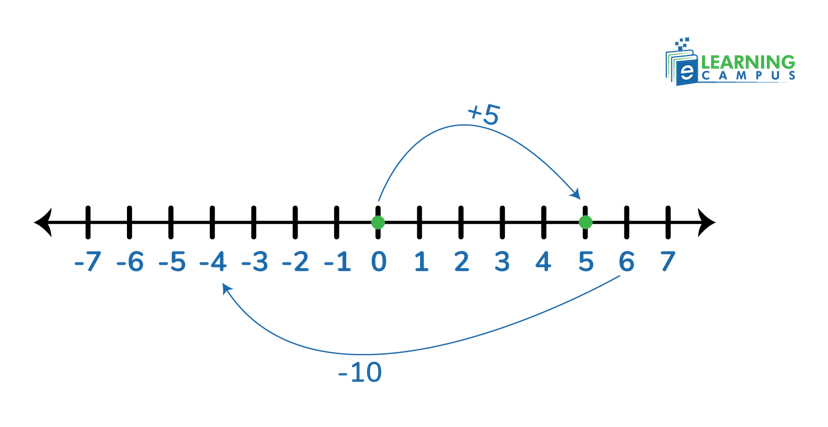
• We landed on -4 after moving the left side.

Properties of integers 

There are several properties in mathematics. These properties show how the numbers behave with mathematical operations. Integers also exhibit several important properties that govern how they behave under addition, subtraction, multiplication, and division. 

closure Property

A set under any operation will be ‘closed’, if performing the operation on that set results in another element within that set. 

Integers are closed under multiplication, subtraction, and addition. This means that when we add, multiply, or subtract two integers, the result will always be another integer. 

For example,

5 + (-3) =2, where 2 is also an integer. 

5 (-4) = -20 which is also an integer. 

Commutative Property

The commutative property of integers states that a change in the position of numbers while performing a mathematical operation does not affect the answer. The commutative property is only applicable to addition and multiplication. 

For example, 

Associative Property 

The associative property states that grouping numbers in an operation does not change the result. This property also applies to addition and multiplication only. 

For example, 

Identity Property 

The identity property of integers is based on identity elements. The identity number for addition is ‘0’, and for multiplication, it is ‘1’. 

This property states that when we add ‘0’ to any integer, it will be equal to the original integer. And when we multiply any integer by ‘1’, it will also be equal to the original integer. 

For example,

Additive Inverse 

The additive inverse states that the addition of any integer with its opposite number will result in zero. For instance,

Multiplicative Inverse Property 

Every integer has a multiplicative inverse (reciprocal) except 0. The multiplicative inverse property of integers states that when we multiply an integer by its multiplicative inverse, the result will be 1. 

For example

The multiplicative inverse of 8 is ⅛. 

When we multiply

Adding and Subtracting Integers Worksheet PDF

Worksheets provide you with an opportunity to exercise the concept practically. The integers worksheet helps you solve problems related to the addition and subtraction of integers. Below you can download the adding and subtracting integers worksheet PDF. Practice it and enhance your problem-solving skills. 

Conclusion 

Integers are the non-fractional numbers. The integers can be positive, negative, or zero. All the arithmetic operations can be performed on the integers. The integers possess certain properties that highlight how they behave under mathematical operations.