Vertical Angles

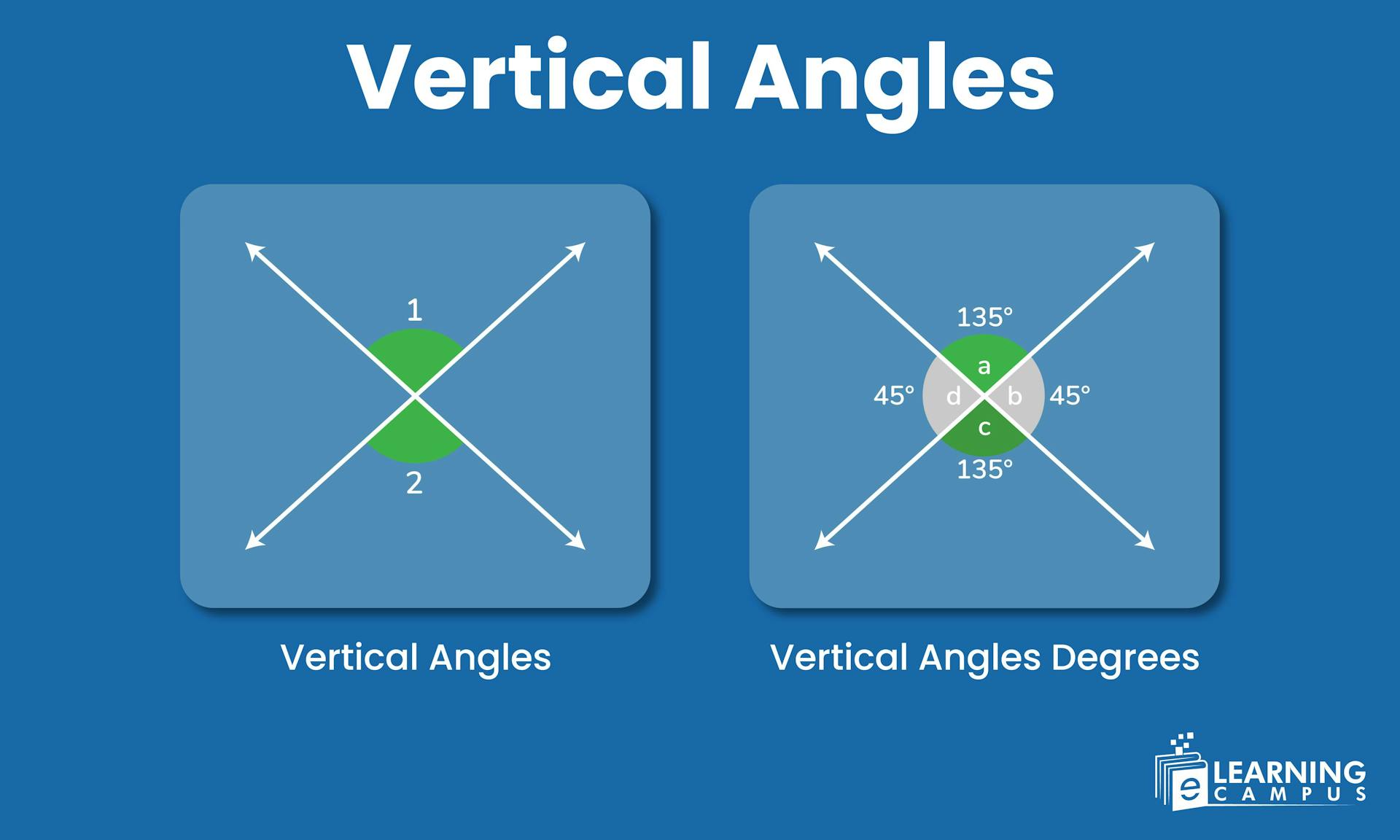
Have you ever noticed how two lines crossing create an "X" shape with angles that face each other from opposite sides? These are called vertical angles. Vertical angles are formed when two lines intersect each other.

In this blog, you will learn what are vertical angles in Math, their theorem with proof, and how to find the measure of these angles. 

What are Vertical Angles

Vertical angles are a pair of non-adjacent angles formed when two straight lines intersect each other. They are also known as vertically opposite angles. They are always congruent (equal in measure) and have the same vertex or corner point. 

Vertical Angles Examples

We know that when two straight lines intersect, four opposite angles are formed. Each of these opposite pair are called a vertical angle. We will understand it with the help of an example. 

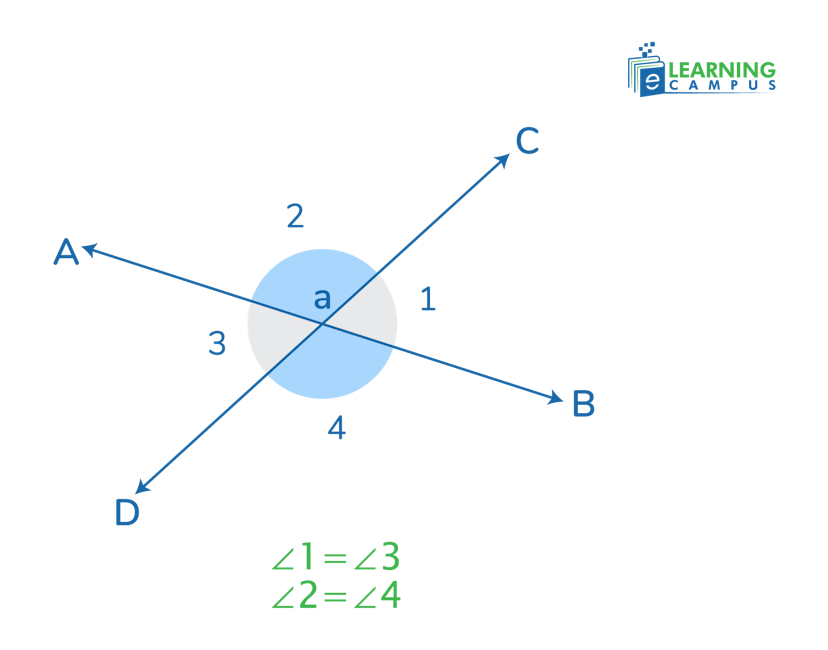
Suppose we have two lines, AB and CD. These two lines intersect at a point O. At the point of intersection, four different angles are formed, i.e, 1,2,3,4 as shown in the image below. 

Out of these angles, the opposite to each other are known as vertical angles or vertically opposite angles. 

• ∠1 and ∠3 are vertical angles 
• ∠2 and  ∠4 are vertical angles 

Vertical Angles Degrees

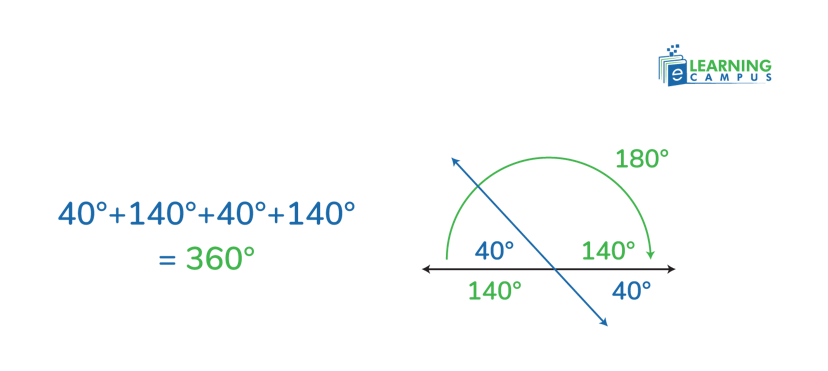
Vertical angles are always equal in measure (congruent), meaning that if one vertical angle is 40∘, its opposite is also 40∘. The four angles formed by the intersection of two lines all add up to 360 degrees. 

For example, 

∠1+∠2+∠3+ ∠4=360

Look at the image below, four angles are formed when two lines intersect. The angles are 40 degrees and 140 degrees. Their sum must be 360 degrees. 

Vertical Angles Theorem

The Vertical Angles Theorem states that when two lines intersect, the angles that are opposite each other, called vertical angles, are congruent or equal in measure. According to the theorem, Vertical angles are always congruent. It means they have the same measure, and they are formed by two intersecting lines, appearing in opposite corners. 

Help your kids learn Math with online expert tutors.

Proof of the Vertical Angles Theorem

We will prove that the vertical angles are congruent.

Given

Two lines intersect, forming four angles. We will call them ∠1, ∠2, ∠3, and ∠4 as shown:

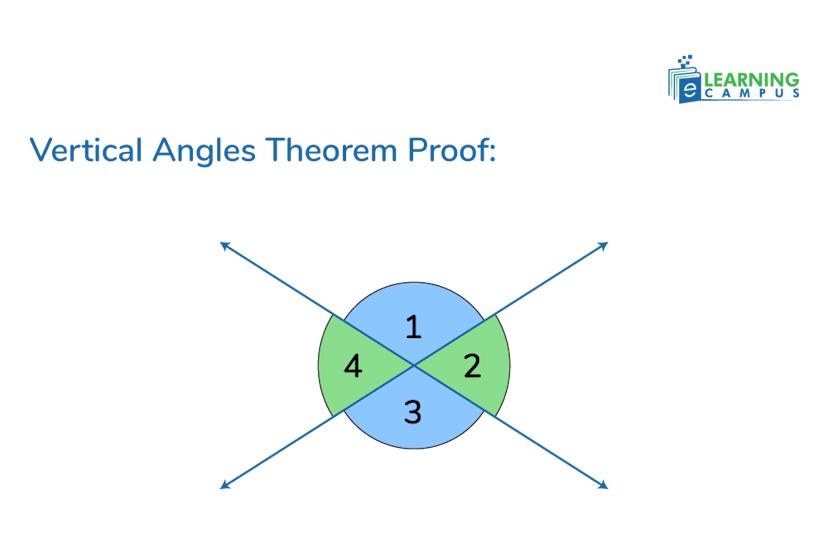
To Prove

∠1 ≅ ∠3 (the vertical angles are congruent)

Proof

Step 1: Identify the linear pairs

When two lines intersect, adjacent angles form a linear pair (they share a side, and their other sides form a straight line).

• ∠1 and ∠2 form a linear pair
• ∠2 and ∠3 form a linear pair

Step 2: Apply the Linear Pair Postulate

The Linear Pair Postulate states that if two angles form a linear pair, they are supplementary (their measures add up to 180°).

Therefore:

• m∠1 + m∠2 = 180° ... (equation 1)
• m∠2 + m∠3 = 180° ... (equation 2)

Step 3: Use the Transitive Property

Since both expressions equal 180°, we can set them equal to each other:

m∠1 + m∠2 = m∠2 + m∠3

Step 4: Apply the Subtraction Property of Equality

Subtract m∠2 from both sides:

m∠1 + m∠2 - m∠2 = m∠2 + m∠3 - m∠2

m∠1 = m∠3

Step 5: Conclude

Since m∠1 = m∠3, we can say that ∠1 ≅ ∠3

Therefore, vertical angles are congruent. 

By the same reasoning, we can prove that ∠2 ≅ ∠4 (the other pair of vertical angles).

Hire online Math tutors for your kids to instill a love for Math in them. 

How to Find Vertical Angles

To find a vertical angle, we can use the principle that vertical angles are congruent (equal). 

• If we know the measure of one angle, its vertical angle is the same. 
• If we are given algebraic expressions for two vertical angles, set the expressions equal to each other and solve for the variable. 

If One Angle's Measure is Given 

• Identify the two intersecting lines.
• Find the angle that is directly opposite the known angle.
• The measure of this opposite, or vertical, angle is the same as the known angle's measure. 

Suppose two lines intersect and one angle measures 40°. Then, the vertical angle opposite the 40° angle also measures 40°.

The adjacent angle measures 180° - 40° = 140°.

The fourth angle (vertical to the 140° angle) also measures 140°. 

If Algebraic Expressions for Two Vertical Angles are Given 

Find the measures of the vertical angles from the expression 12x + 10 = 5x + 31

Since vertical angles are equal, set the two expressions for the angles equal to form an equation.

Solve for the variable: Isolate the variable by using algebraic properties of equality.

Subtract 5x from both sides

12x + 10 = 5x + 31

12x + 10 -5x= 5x -5x+ 31

7x + 10 = 31

7x = 21

x = 3

Substitute the value of the variable back into the original expressions to find the angle's measure.

Using the first expression 12x + 10

12(3) + 10

36 + 10=46

Using the second expression 5x + 31

 5(3) + 31

 15 + 31=46

So, the measurement of the vertical angle is 46 degrees. 

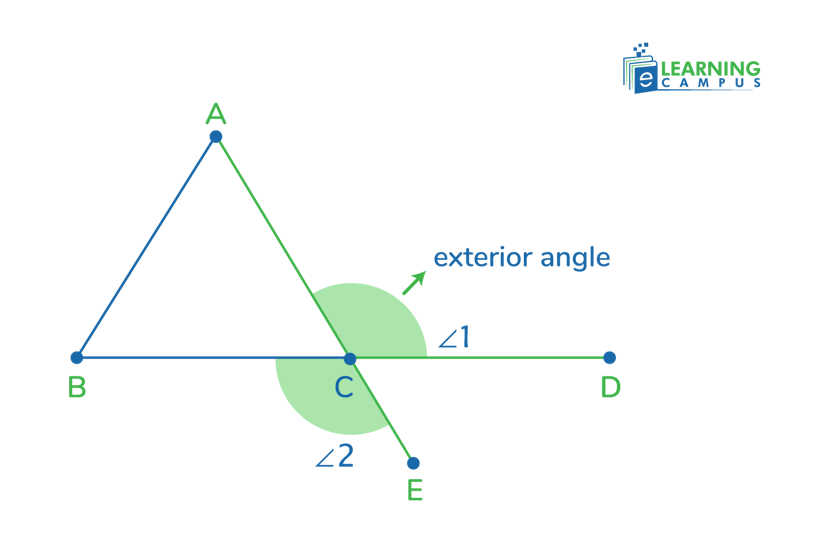
Vertical Angles of a Triangle 

In the context of a triangle, the concept of vertical angles is typically used when we deal with Exterior Angles. When we extend one side of a triangle, we form an exterior angle. The two exterior angles at any single vertex of a triangle are vertical angles to each other and thus have equal measure.

Look at the triangle ABC below. 

If we extend line BC to D, an exterior angle will form, which we will call ∠1. If we extend the line AC to E, another exterior angle will form, which we will call ∠2. Point C acts as the common vertex for ∠1 and  ∠2. 

So, in this triangle, the ∠1 and  ∠2 are vertical angles because they are formed by the intersection of the two lines AE and BD. They will also be equal in measurement (congruent). 

Are Vertical Angles Congruent

Yes, vertical angles are always congruent (equal in measure). Congruent means they have the same measure. So:

• If one vertical angle is 40°, the other is 40°
• If one vertical angle is 127°, the other is 127°
• If one vertical angle is x°, the other is x°

This is not just sometimes true, it is a fundamental geometric truth that holds in every case where two lines intersect. If two angles are vertical angles then they are congruent. 

Why are Vertical Angles Always the Same

When two lines intersect, they create two pairs of vertical angles. The opposite angles are congruent to each other, known as the vertically opposite angles. Vertical angles are always the same due to a geometric principle known as the Vertical Angles Theorem. This can be proven using the properties of a straight line and supplementary angles.

Are vertical angles complementary?

Vertical angles are not necessarily complementary, but they can be in a specific case. 

Complementary angles are any two angles whose measures add up to 90 degrees, regardless of their position. 

Vertical angles are only complementary if each of the angles measures exactly 45 degrees (because 45 + 45 = 90). In all other cases, they will not be complementary. 

Worksheet on Vertical Angles

Vertical angles worksheets are an educational resource, typically a printable PDF. It is designed to help students practice identifying and calculating the measures of vertical angles formed by intersecting lines. 

The core principle applied in these worksheets is the Vertical Angles Theorem. You can practice vertical angle problems in these worksheets. 

We provide you with the printable worksheet on vertical angles in PDF.

Conclusion 

Vertical angles are pairs of opposite angles formed by two intersecting lines. They are always equal in measure (congruent) and share a common vertex (point of intersection). They look like an "X" or a cross, with the angles directly across from each other being the vertical pairs.