What are Math Properties  

Have you ever wondered why 3+5 is always equal to 5+3 or why multiplying a number by 1 never changes a number? Mathematics is more than just numbers and equations. There are some rules and patterns on the basis of which numbers are operated. Mathematics follows a set of special rules called the mathematical properties of operations. These properties describe how numbers behave in different operations, ensuring consistency and logic in every calculation.

In this blog, we will explore the main types of properties in math, their definitions, and examples that make them simple to understand.

What are the Properties in Math 

A math property is a law or rule that describes how numbers work in different operations. These properties never change. They are true for all real numbers. If we understand them, then math becomes riser, more logical, and less confusing. Basic properties of operations in math are : 

• Commutative property 
• Associative property 
• Distributive property 
• Identity property 
• Inverse property 
• Zero Property of Multiplication 

Commutative property 

The commutative property tells us that the order of numbers does not change the result. It states that numbers can be rearranged in an operation without changing the outcome.

This property works for addition and multiplication but not for subtraction or division.

For  addition 

For  Multiplication 

Get help with our online math tutoring service 

2.Associative Property

The associative property explains that when you add or multiply three or more numbers, the way you group them doesn't change the result.

For Addition 

For Multiplication 

The grouping doesn't affect the result.

3. Distributive Property

The Distributive property links multiplication and addition. It explains that multiplying a number is multiplying each addend separately and then adding the products. It explains that multiplying a number sum gives the same result as multiplying each addend separately and then adding the products. The distributive property is used frequently in algebra to simplify and expand expressions.

$$3 \times (2 + 2) = (3 \times 2) + (3 \times 2)$$

4. Identity Property 

The Identity property shows that certain numbers keep others unchanged when used in an operation.

Addition Identity 

0 is the identity property because adding it does not change a number 

For Example 

Multiplication Identity

1 is the multiplicative identity because multiplying by it does not change a   number 

For Example 

5.Inverse property 

The inverse property tells us that every number has an opposite or reciprocal that brings it back to the identity value. This property helps in simplifying and balancing the equations.

Additive inverse 

For example 

 Multiplicative Inverse 

Example

$$=1 $$ 

Zero property of Multiplication 

This property is simple yet powerful. When you multiply any number by zero, the answer is always zero.

For example 

Properties of Equality in Math 

Other properties are widely used. The property of equality helps us understand how numbers relate to each other when they are equal. They are often used when we are solving an equation. These  properties include:

• Symmetric property 
• Reflexive property 
• Transitive property 

Symmetric property 

The symmetric property states that if one expression is equal to another, then the other expression is also equal to the first one.

For example 

a=b,b=a

Reflexive equality 

The reflexive property states that any quantity is equal to itself.

a=a

Transitive property 

The transitive property states that if the first value is equal to the second, the second value is equal to the third, and the third value is equal to the first.

a=b, b=c, a=c

All Math properties Examples 

Learn the math properties with examples, which help you understand how numbers behave in every operation.

• Commutative property 

In addition

 In multiplication 

• Associative property

In addition 

In Multiplication 

• Distributive property 

$$3\times(2+2) = ( 3\times2) +(3\times2 )

• Identity property 

In addition 

In multiplication 

• Inverse property

Additive inverse 

Multiplicative inverse 

• Zero property of multiplication

If we multiply any value by zero, then the answer is always zero. 

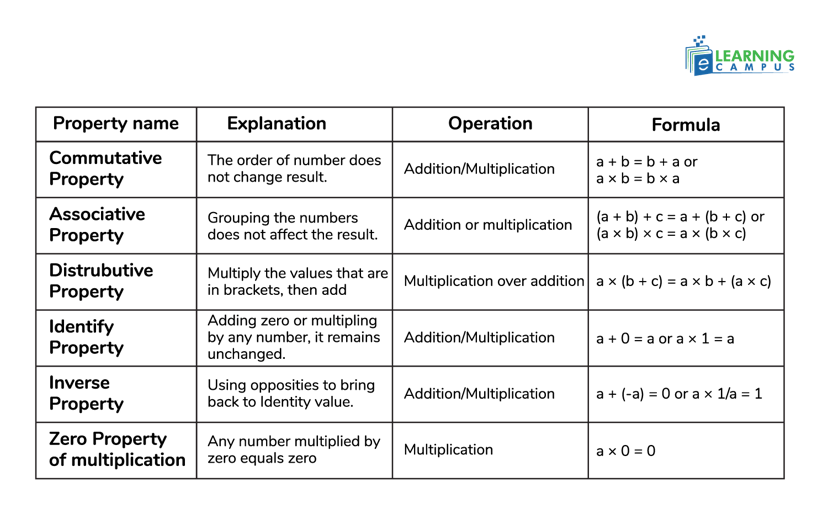
Math Property Chart 

A math property chart is a simple and visual way to show the basic rules that numbers follow during mathematical operations. It lists the main properties along with their Formula and examples.

This chart helps you quickly remember how each property works. Here are the math property chart:

Conclusion 

Math properties are the foundation of arithmetic and algebra. They describe how numbers perform in different operations, like addition or multiplication. In our blog, we provide detailed information on basic properties of math with examples that help you understand the math easily and strengthen your basic knowledge for higher mathematical concepts. Once you know these rules, math becomes logical and much easier to handle.