Triangle Congruence Worksheet


Two triangles with the same size, shape, and angle are called congruent triangles. It means all three corresponding parts of congruent triangles and all three corresponding angles of the triangles are equal. The triangle congruence worksheet is an effective tool in understanding and identifying congruent triangle.
Two triangles are said to be congruent if they have the same size and shape. This means their corresponding sides are equal in length, and their corresponding angles are equal in measure. Corresponding parts of congruent triangles are congruent.
Congruent triangles can be identified through a variety of rules and shortcuts, known as the congruence postulates.
Proving the congruency of triangles can be a lengthy process. The triangle congruence postulates and theorems provide shortcuts to prove that two triangles are congruent without needing to prove all corresponding angles and sides are equal.
The main postulates and theorems of congruent triangles include Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), Angle-Angle-Side (AAS), and the Hypotenuse-Leg (HL) theorem.
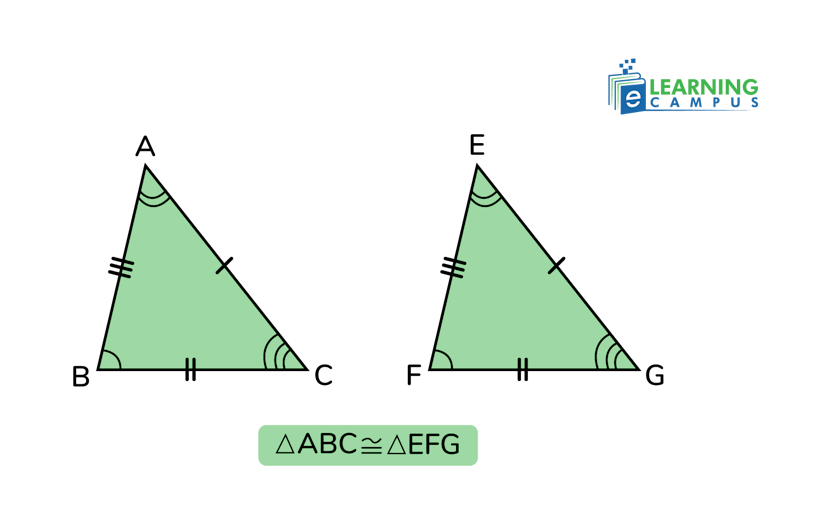
The sss congruence postulate, or side side side congruence postulate, states that ‘if three sides of a triangle are equal to the sides of another triangle, then the triangles will be called congruent triangles.
For example, in the two triangles below, the sides AB are equal to DE, AC is equal to DF, and BC is equal to EF.
AB = DE, BC = EF, and AC = DF
So, ∆ABC ≅ ∆DEF
Hence, the triangles congruent by SSS postulate are proved.
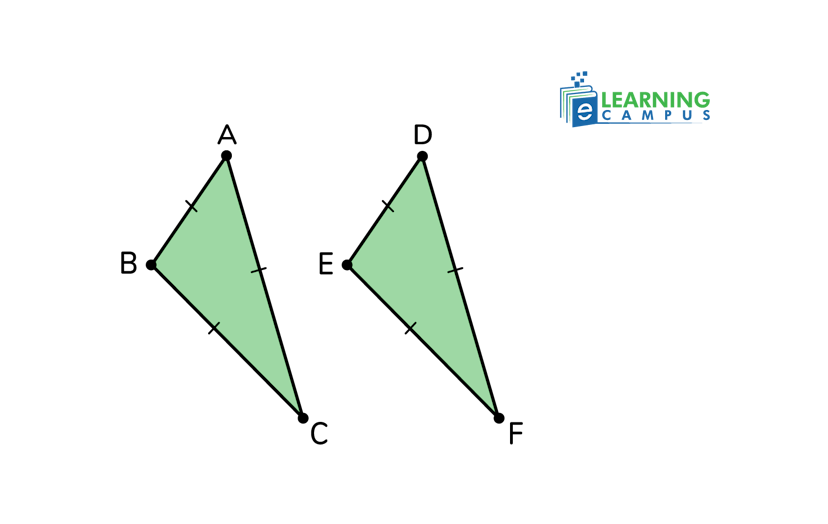
The postulate SAS, or the side-angle-side postulate, states that ‘if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.’
In the two triangles below,
RS ≅UV
TR ≅VU
∠R ≅∠U
So, TRS ≅WUV
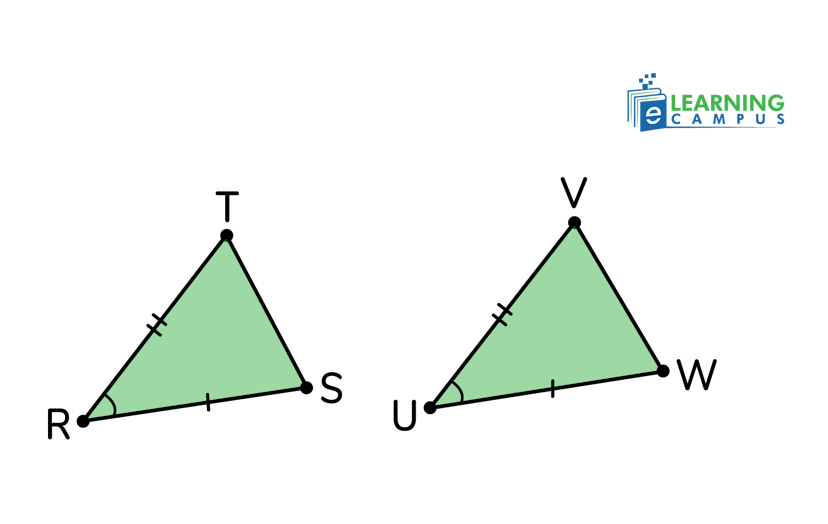
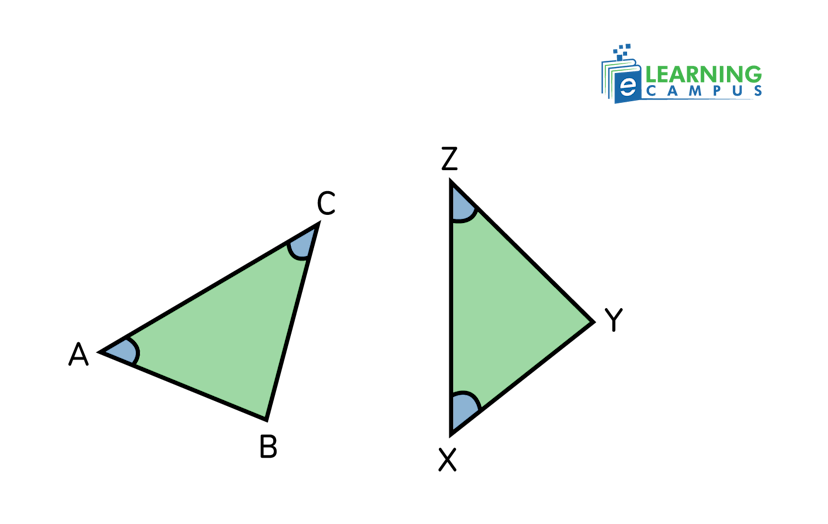
The angle-side-angle, or ASA postulate states that if two angles and the included side of one triangle are congruent to the corresponding two angles and included side of another triangle, then the triangles are congruent.
In the triangles △ABC and △XYZ given below,
∠CAB≅∠ZXY
AB≅XY
∠ACB≅∠XZY
Which shows two triangles that are congruent by the ASA postulate.
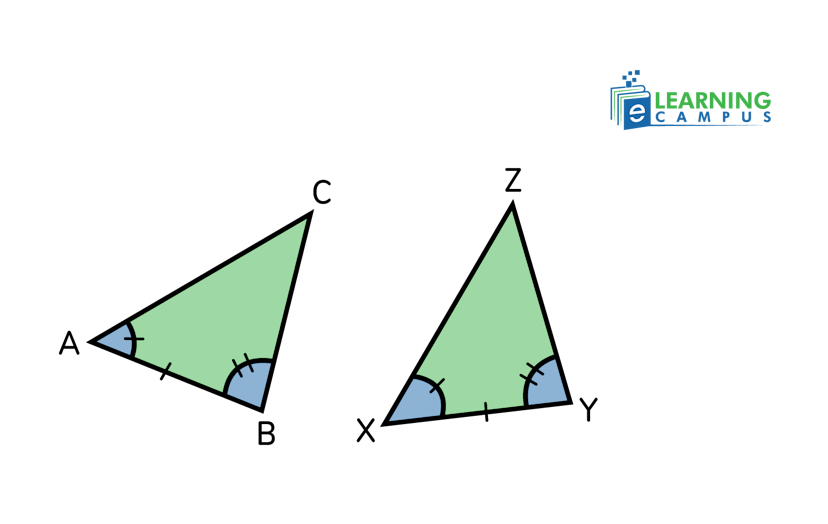
The AAS, or angle-angle-side postulate, states that if two angles and a non-included side of one triangle are congruent to the corresponding two angles and non-included side of another triangle, then the triangles are congruent.
In the triangles given below,
∠A≅∠X
∠B≅∠Y
AB≅XY
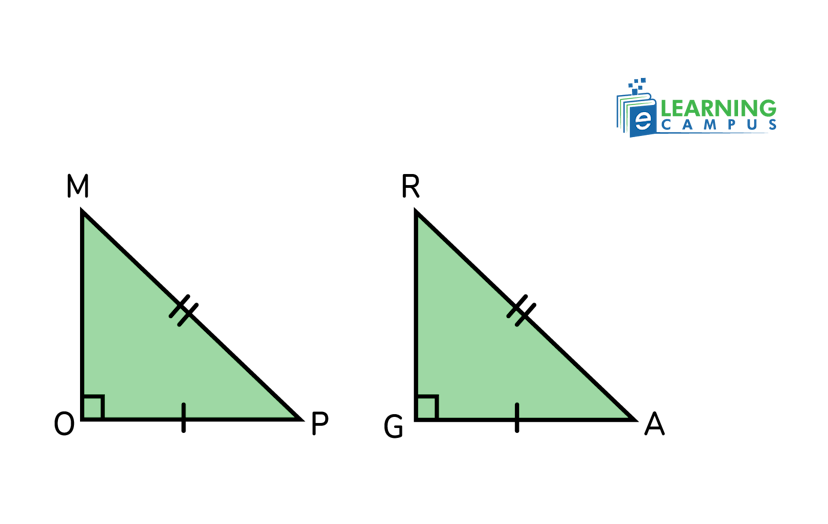
The hypotenuse-leg or HL triangle congruence theorem is a special case of the right triangle. It states that ‘if the hypotenuse and one leg of a right triangle are congruent to the corresponding hypotenuse and leg of another right triangle, then the two triangles are congruent.’
In the given triangles,
MP ≅ RA
OP ≅ GA
Worksheets are effective tools that turn abstract ideas into engaging, accessible learning experiences. We provide you with the triangle congruence worksheet to help you understand the congruence of triangles and be able to recognize the congruent triangle easily. You can download the congruence of triangles worksheet PDF format.
Are you looking for expert math online tutors to teach kids? We are at your service. We have expert math teachers with years of experience in teaching math online. You will get an expert instructor of the subject.
