elearning BlogSymmetric Property

Symmetric Property

Symmetric Property

Have you ever noticed how some truths in mathematics work both ways, like a perfect reflection in a mirror? If your friend is standing next to you, then you're standing next to your friend. This beautifully simple idea lies at the heart of one of mathematics' principles known as the symmetric property. 

This concept has several uses in maths. The symmetric property states that if one expression is equal to another, then the other expression is also equal to the first one. This simple rule keeps equality, congruence, and even geometry balanced and logical.

In this blog, we will learn about the symmetric properties of equality, congruence, matrices, and geometry with different examples for better understanding.

What is the Symmetric Property?

The symmetric property states that if one relationship is valid on one side, then it must be valid on the other side. For Example, a=b then b=a. 

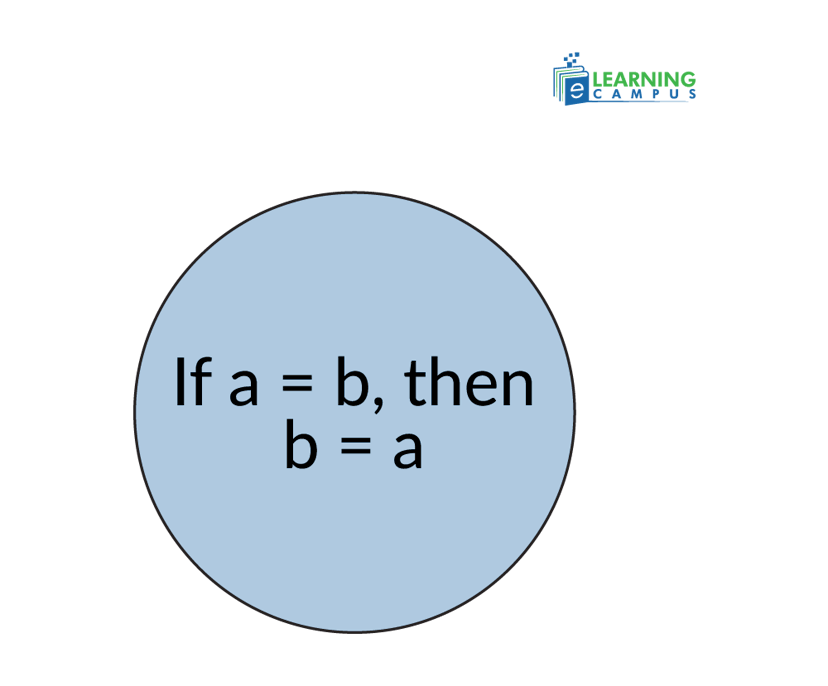
What is the Symmetric Property

Various forms of Symmetric properties are : 

  • Symmetric Property of Equality
  • Symmetric property of congruence 
  • Symmetric Property of Matrices
  • Symmetric Property of Geometry

What is a Symmetric Property of Equality?

In simple words, the symmetric property of equality states that: if one quantity is equal or congruent to another, then the reverse is also true. Here are some examples of the symmetric property of equality :  

  • Symmetrical Property in Arithmetic 

If    4+2=6then 6=4+2

  • Symmetrical property in Algebra

If x=3 then 3=x 

  • Symmetrical Property in a Matrix 

If A=ATthe matrix is symmetric

  • Symmetrical property in congruence  

If ABC=DEF  then DEF=ABC

This concept is called the symmetric property of equality. It shows that equality works on both sides and makes sure that mathematical statements stay balanced and true.

Symmetrical Property of Geometry

In geometry, the symmetric property means that if one geometric figure is equal to or is congruent to another, then the reverse is also true.

It is used when proving, shapes, angles, and triangles are congruent

For example: 

  • If line AB =line CD, then line CD =line AB

Symmetrical Property of Congruence:

The symmetric property of congruence states that if one shape is congruent to another, then the second shape is also congruent to the first one.

For Example:

  • If line segment AB≅CD, then CD≅ AB. 
  • If another example of triangle ABC is congruent to triangle DEF, then triangle DEF is also congruent to triangle ABC.
  • This property helps prove geometric theorems and supports logical reasoning in proofs.

Symmetrical Property of Matrix:

The symmetric property of a matrix states that if a matrix B is symmetric, then it is equal to its transpose.

For example : 

B=BTB=B^T
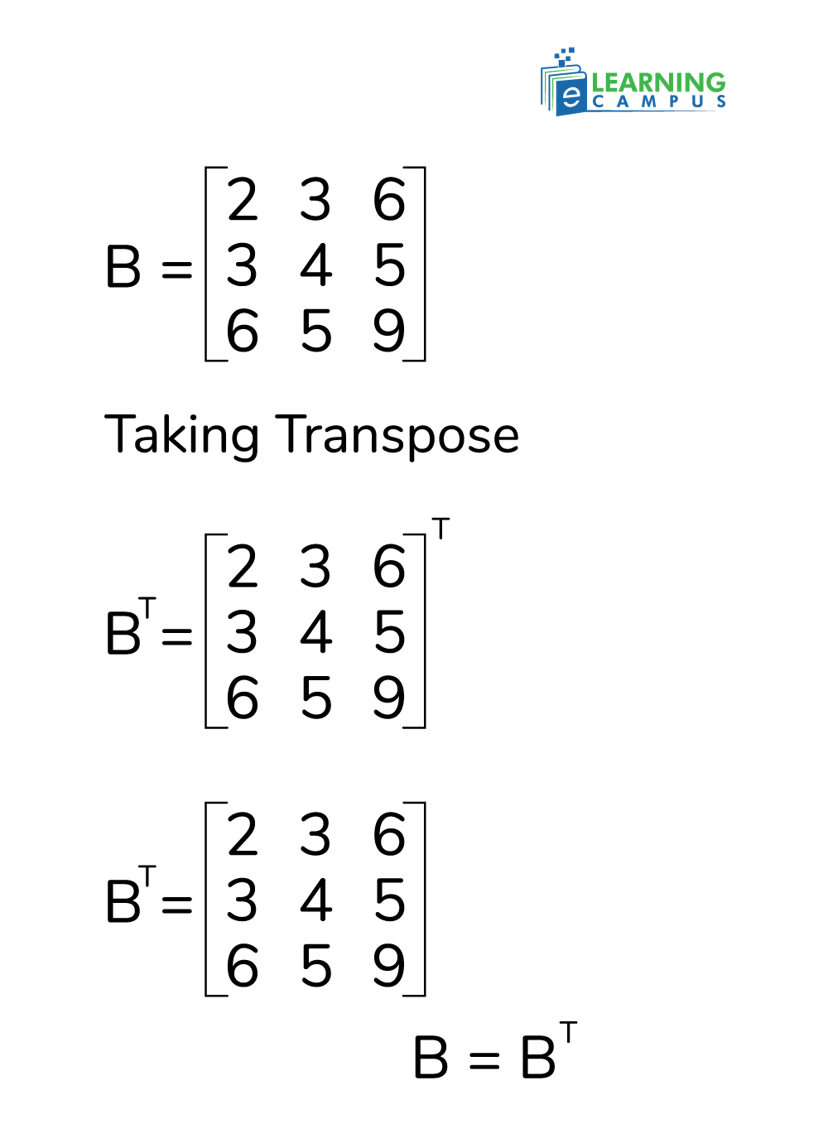
Symmetrical Property of Matrix

In this Example, there is a matrix B. Now we take the transpose of matrix B, which means changing rows into columns and columns into rows. After taking the transpose, the matrix is equal to B, which means Matrix B is symmetric.

Properties of a Symmetric matrix 

Some key properties of asymmetric matrix are : 

  • Symmetric matrices are commutative, which means that if A and B are symmetric matrices, then AB=BA
  • The Sum or difference of two symmetric matrices also results in a symmetric matrix.
  • The elements across the diagonal are equal.
  • If B is symmetric, then B^T also symmetric.
  • If B is a symmetric matrix, then B^2 so is also symmetric.

Skew-symmetric Matrix: 

A skew-symmetric matrix states that the Transpose of A is equal to its negative. For example 

Skew-symmetric Matrix
BT=−BB^T=-B

In this example, we see that the transpose of B is equal to -B, which satisfies the skew-symmetric property.

Symmetric Matrix Determinant

The determinant of a symmetric matrix states that for a symmetric matrix A, its determinant is equal to the determinant of its transpose, 

det⁡(A)=det⁡(AT)\det(A) = \det(A^T)
  •  Determinant can be calculated using cofactor, row/column operations, or eigenvalues. 
  • The special numbers associated with a square matrix A that tell us how the matrix stretches or compresses vectors along certain directions are called eigenvalues.

Mathematical form :

Av=λvA\mathbf{v} = \lambda \mathbf{v}
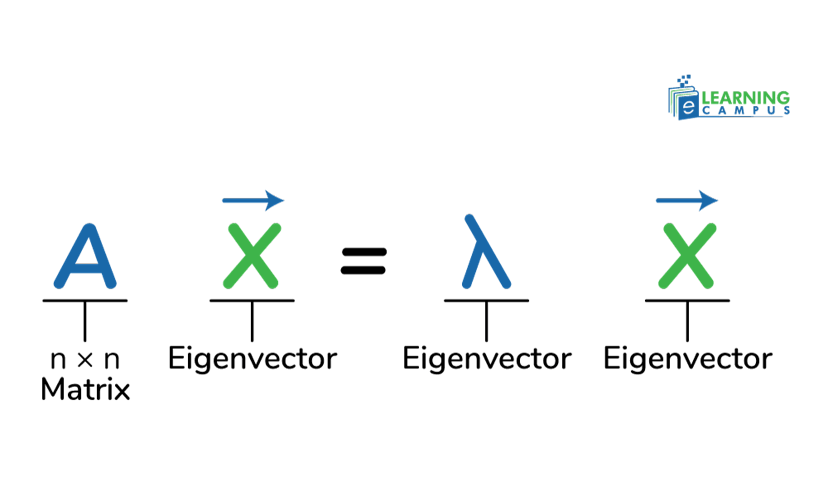
Symmetric Matrix Determinant
  •  It does not change the direction only shows how much the matrix stretches, shrinks, or flips its special vectors.

For example 

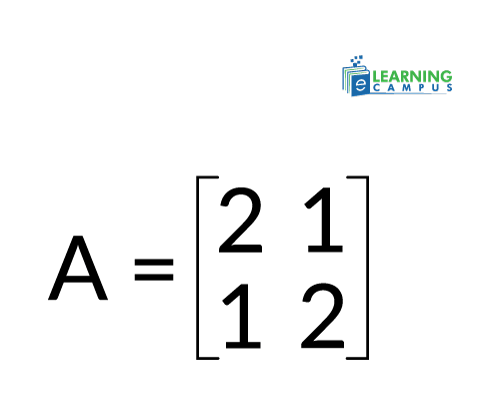
Symmetric Matrix Determinant- example

Step 01: Write the equation 

Eigenvalues() satisfy the equation: 

Av=λvA\mathbf{v} = \lambda \mathbf{v}

Which means

det⁡(A−λI)=0\det(A - \lambda I) = 0

Here : 

A=matrixA = \text{matrix}
I=identity matrixI = \text{identity matrix}
λ=eigenvalue\lambda = \text{eigenvalue}

Step 02 :  (A-I) write in matrix form

Subtract λ from each diagonal element 

Step 03: Find the determinant 

Write Determinant of  (A-I) is equal to zero

det⁡(A−λI)=0\det(A - \lambda I) = 0
det⁡[2−λ112−λ]=0\det \begin{bmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \end{bmatrix} = 0
(2−λ)(2−λ)−(1⋅1)=0(2-\lambda)(2-\lambda) - (1 \cdot 1) = 0

Step 04: Simplify

Shift the 1 to the other side, now it becomes positive 1.

Step 05: Take the square root 

Now take the square root, which cuts the square and remains:

(2−λ)2=1\sqrt{(2 - \lambda)^2} = 1
2−λ=±12 - \lambda = \pm 1

Step 06: Solve for 

Now simplify it to find the eigenvalues 

2−λ=1or2−λ=−12 - \lambda = 1 \quad \text{or} \quad 2 - \lambda = -1
2−λ=12 - \lambda = 1
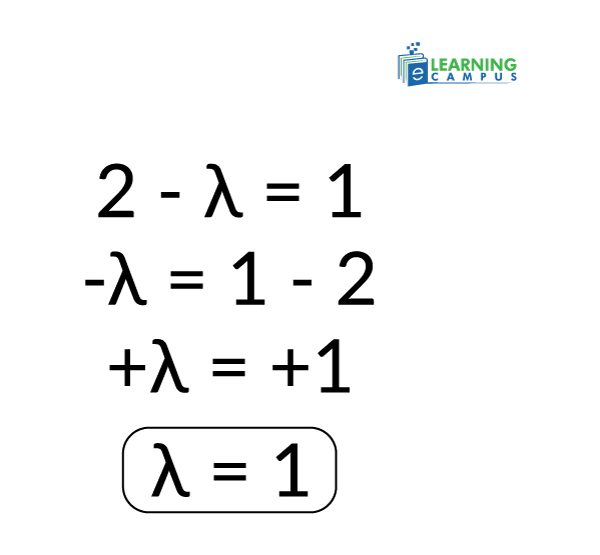
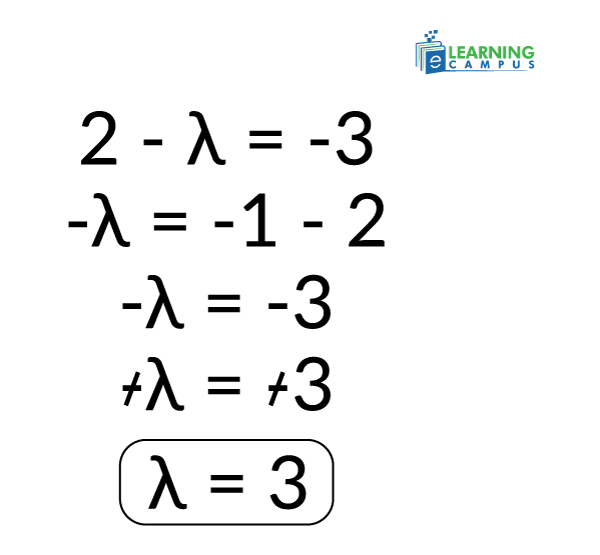
Symmetric Matrix Determinant- example
λ=1\lambda = 1
2−λ=12 - \lambda = 1
Symmetric Matrix Determinant- example

So, Eigen values are

Eigenvalues:λ1=1,λ2=3\text{Eigenvalues:} \quad \lambda_1 = 1, \quad \lambda_2 = 3

Properties of the Symmetric matrix determinant:

  • The determinant is always real.
  • Determinant is equal to determinant of its transpose, e.g,
det⁡(A)=det⁡(AT)\det(A) = \det(A^T)
  • If all eigenvalues are positive, then the determinant is greater than zero.
  • Determinant helps to identify the matrix type. If the determinant is equal to zero and the matrix is singular, or if the determinant is not equal to zero, the matrix is invertible (non-singular).

Properties of Skew-Symmetric Matrix 

Some properties of a skew-symmetric matrix are:

  • All the diagonal elements on the main diagonal must be zero, 
  • The corresponding off-diagonal elements are negative of each other.
  • The transpose is equal to the negative of the matrix.
  • Only a square symmetric matrix can be skew-symmetric.

What is the Reflexive Property 

A Reflexive property states that any quantity is equal to itself. This property is used when two geometric figures share a common side or angle. Here are various reflexive properties.  

  • Reflexive Property in Arithmetic 

It states that any number is equal to itself.For example 7=7,-5=-5 

  • Reflexive Property in Algebra

It states that any two algebraic expressions are always equal to themselves. For example,

(3+y)=(3+y)(3 + y) = (3 + y)
  • Reflexive Property in Congruence  

It states that any geometric figure is congruent to itself. For Example ;

Line  AB≅line  AB.

  • Reflexive Property in Matrix 

It states that the matrix is equal to itself 

A=A

For Example 

What is the Reflexive Property

Transitive Property

A transitive property states that any value that is equal to the second one, the second value is third the and the first equals the third. It shows a chain relationship between the first and last value.

For example 

x=y=2  ⟹  x=2x = y = 2 \quad \implies \quad x = 2

Differentiate Symmetric, Reflexive, and Transitive Properties 

 The main differences between the symmetric are: 

The Symmetric property means that if one value is equal to the first, then the second value is equal to the first. 

For example

A+B=B+AA+B=B+A
  • It compares two different values.
  • It shows reversible equality.

The Reflexive property means that any value is equal to itself. 

For example A=A

  • It compares its value with itself. 
  • It shows self-equality. 

The Transitive property means that if one value is equal to the second value, the second value is equal to the third value, then the first value is equal to the third value. 

For example : 

a=bb=c a=ca=b b=c  a=c
  • It compares three different values. 
  • It shows chain equality. 

Conclusions 

The symmetric property shows that if one value is equal to the second, then the second value is equal to the first one. This property helps you to find the variables in equations. In our blog, we clearly mentioned the details of each type of symmetric property that helps you to understand the matrix and eigenvalues in an easy way.

Learn math online with expert Tutors.

Do you find symmetric property and their various types hard to learn? Don't worry, our expert online math tutors are here to help you. Explore easy-to-follow lessons, clear examples, and practical exercises that strengthen your understanding of math. Get benefits with our online tutoring service and start easily learning math.

Hire online math tutor
Hire a Tutor Now!

FAQs