Perfect Squares in Math 

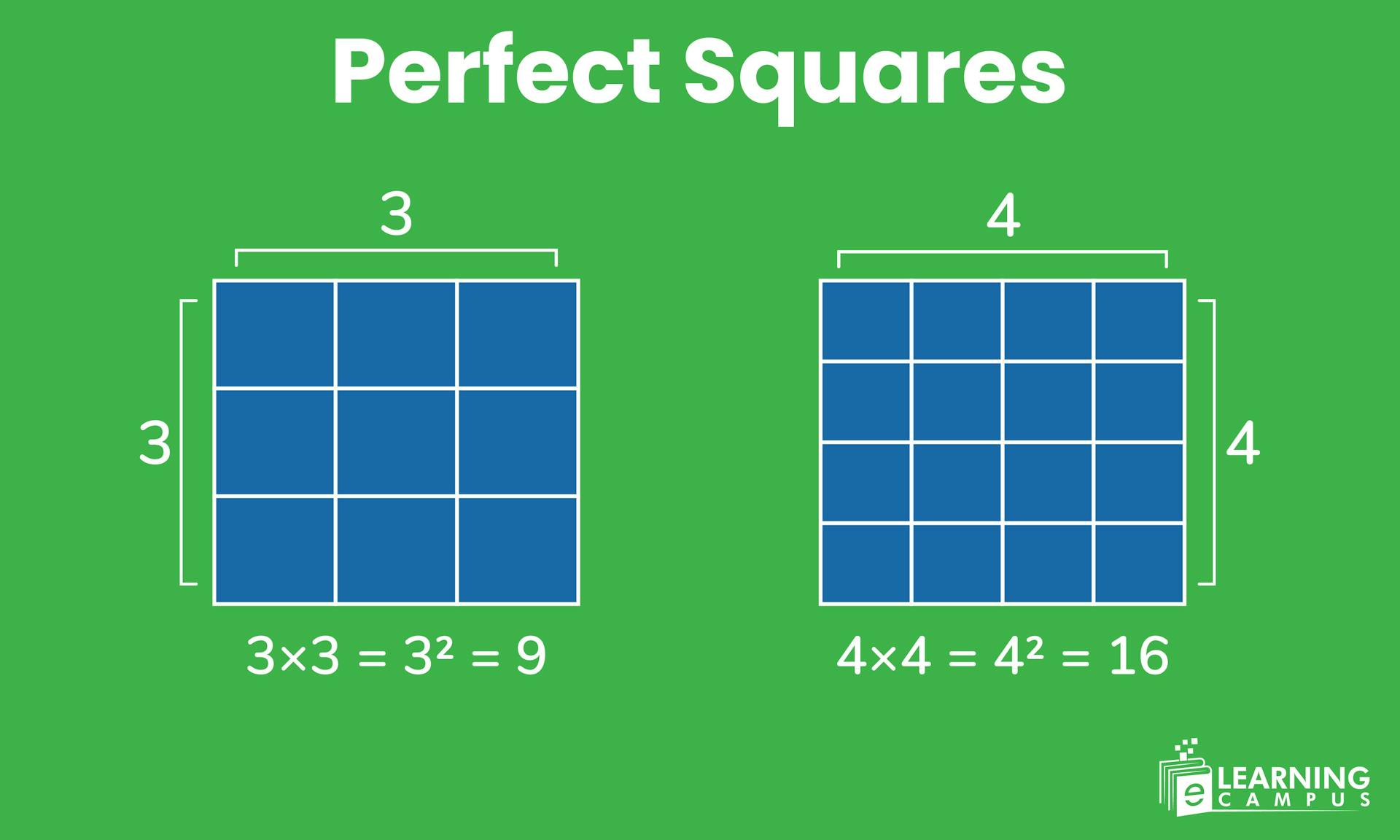
You are aware of the squares, but have you ever heard about the perfect square? We use this concept recurrently in our daily lives. The perfect square numbers are the product of two equal integers. 

In this blog, you will learn about perfect squares with clear definitions, easy-to-use tips, and how to identify perfect squares. 

What are Perfect Square Numbers

A perfect square number, or square number, is a positive integer that results from multiplying another integer by itself. In simple terms, a perfect square is any number you get when you multiply a whole number by itself. 

Perfect Square Examples

We will understand the perfect squares with the help of examples from our daily lives. 

Consider, we have 4 marbles in one group and 6 marbles in another. Now try arranging them into neat shapes. 

With your 4 marbles, we can make a perfect square by arranging them in 2 rows with 2 marbles in each row. It forms a nice, even square shape. 

With 6 marbles, we can only make a rectangle by arranging 2 rows with 3 marbles in each row. No matter how we try, we cannot make a square. 

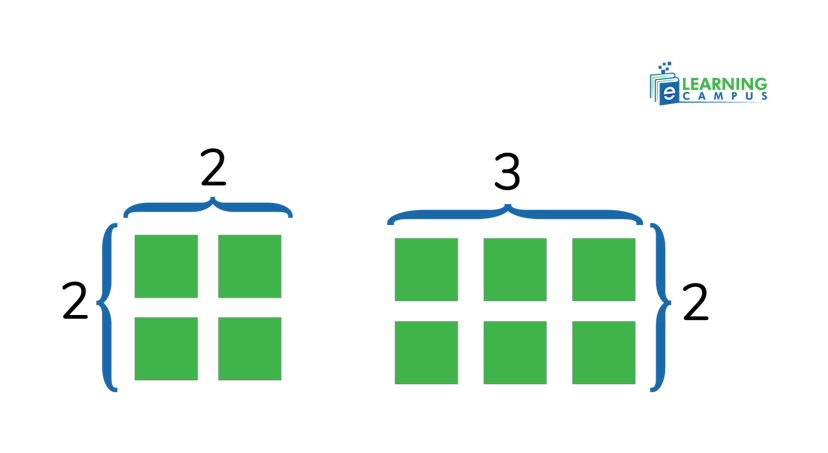
Here's the math behind it:
4 marbles = 2 × 2 = 2², makes a square.
6 marbles = 2 × 3, makes a rectangle, not a square.
The number 4 is special because it comes from multiplying the same number by itself (2 × 2). That is what makes it a perfect square.

Perfect Square Formula

The ‘perfect square formula’ refers to a specific number (integer) that can be expressed as the square of another integer.
The formula for a perfect square is expressed as:
n² = n × n
Where n is any whole number (0, 1, 2, 3, 4, 5...)
When you multiply any whole number by itself, you get a perfect square. Examples:
1² = 1 × 1 = 1
2² = 2 × 2 = 4
3² = 3 × 3 = 9
4² = 4 × 4 = 16
5² = 5 × 5 = 25
10² = 10 × 10 = 100

How to Find the Perfect Square of a Number

To find the perfect square of any number, simply multiply that number by itself or square it.
For example,
The perfect square of 6 is 6 × 6 = 36
The perfect square of 9 is 9 × 9 = 81
The perfect square of 10 is 10 × 10 = 100

How to Identify if a Number is a Perfect Square

There are several methods to determine if a given number is a perfect square. The famous methods include:

Square Root Method 

The square root method is the most direct method to determine if a number is a perfect square. It includes the following steps. 

• Calculate the square root of the given number.
• Check if the result is an integer (a whole number).
• If the result is an integer, the original number is a perfect square. If the result is a decimal, it is not a perfect square.

Example:
Determine if 49 is a perfect square.
To determine, we will take the square root of 49.
√49 = 7
The square root of 49 is 7, which is an integer, so 49 is a perfect square.

Identify if 35 is a perfect square.
We will take the square root of 35.
√35 ≈ 5.916
The square root of 35 is approximately 5.916, which is a decimal, so 35 is not a perfect square.

Prime Factorization Method

• Find the prime factors of the number.
• Check the exponents of each prime factor.
• If all the exponents are even numbers, then the number is a perfect square.

Example:
Find if 144 is a perfect square.
We will find the prime factors of 144.

The prime factorization of 144 is 2 × 2 × 2 × 2 × 3 × 3, or 2⁴ × 3². Since both 4 and 2 are even exponents, 144 is a perfect square.

Look for Patterns and Properties (Quick Tips)

By looking at the pattern of numbers, we can identify whether they are perfect squares or not. 

• Ending digits: A perfect square always ends in 0, 1, 4, 5, 6, or 9. If a number ends in 2, 3, 7, or 8, it is not a perfect square.
• Number of zeros: If a number ends with zeros, there must be an even number of them to be a perfect square (e.g., 100 is a perfect square, but 1000 is not).

Is 2 a Perfect Square

No, 2 is not a perfect square. 

A perfect square is an integer that can be obtained by multiplying another integer by itself. 

• 1×1=1, so 1 is a perfect square.
• 2×2=4, so 4 is a perfect square. 

The number 2 falls between 1 and 4, and there is no whole number that, when multiplied by itself, equals 2. The square root of 2 is approximately 1.414, which is not an integer, confirming that 2 is not a perfect square. 

Is 10 a Perfect Square

No, 10 is not a perfect square. 

A perfect square must be the result of squaring an integer. 

• 3×3=9
• 4×4=16

The number 10 falls between 9 and 16. There is no integer that, when squared, equals 10. The square root of 10 is approximately 3.162, which is not a whole number.

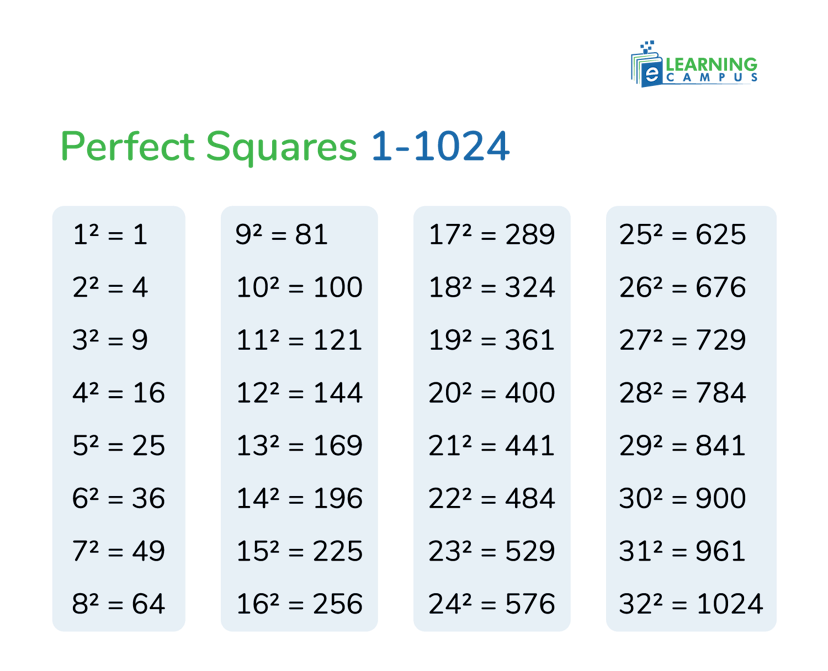
Perfect Squares List

A list of perfect squares includes the first few numbers. Below is the list of perfect square numbers from 1 to 1042. 

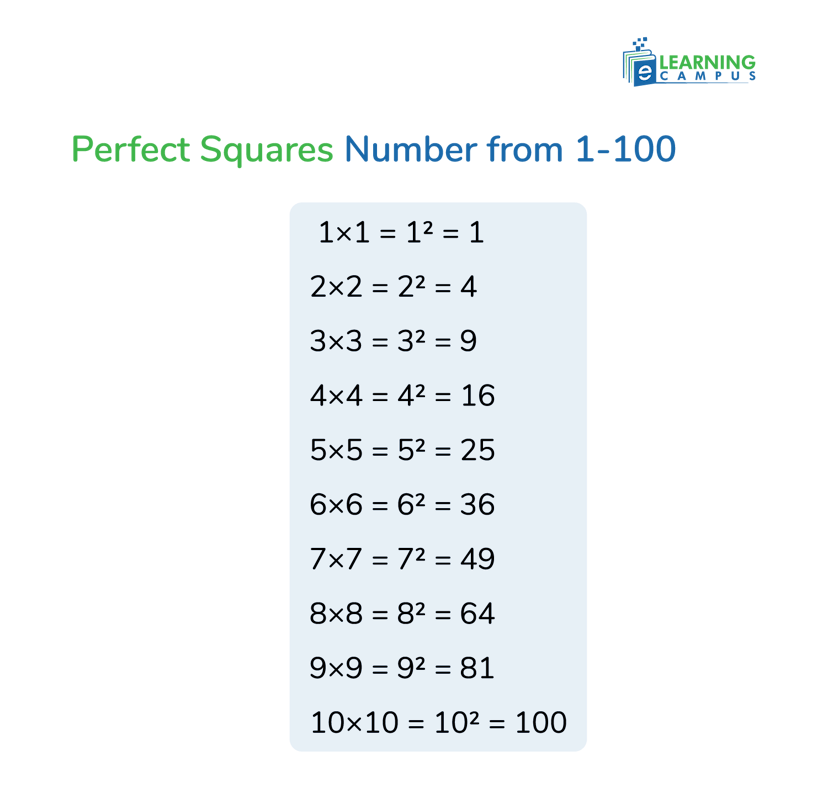
Perfect Squares 1-100

The perfect squares from 1 to 100 are the results of squaring each integer from 1 to 10. There are ten such perfect squares from 1-100, as listed below;

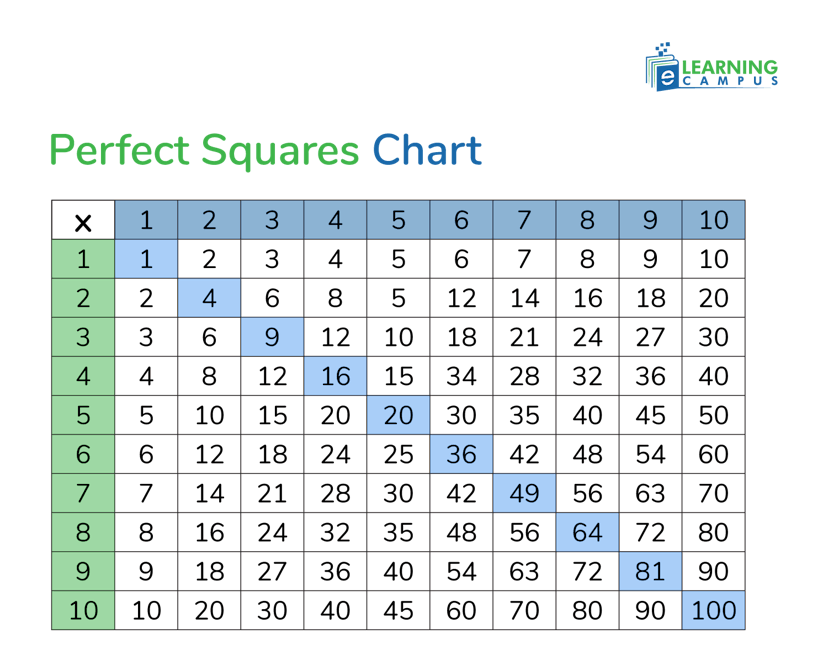
Perfect Squares Chart

A perfect squares chart is a reference table or list that displays the results of squaring whole numbers or integers, visually organizing the perfect square numbers. 

Below is the perfect squares chart from 1-100.

Conclusion 

A perfect square is a whole number that is the product of an integer multiplied by itself. These numbers have an integer square root, and their properties are used in various mathematical areas like algebra and number theory.