elearning BlogLaw of Sines 

Law of Sines 

law of sines

The law of sines relates the ratio of lengths of the sides of the oblique triangle to the sines of its respective angles. The sine law helps find the unknown side or angle of an oblique triangle. The sine rule can also be understood as the ratio of the sine of any angle in a triangle to its opposite side is the same for the angles in the triangle.

What is the Law of Sines? 

The law of sines and the law of cosines are two important concepts in trigonometry to solve problems concerning the angles and sides of the triangle.

In simple terms, the sine law states that the sides of any triangle are proportional to the angles that lie opposite to that side. 

The law of sines definition states that;

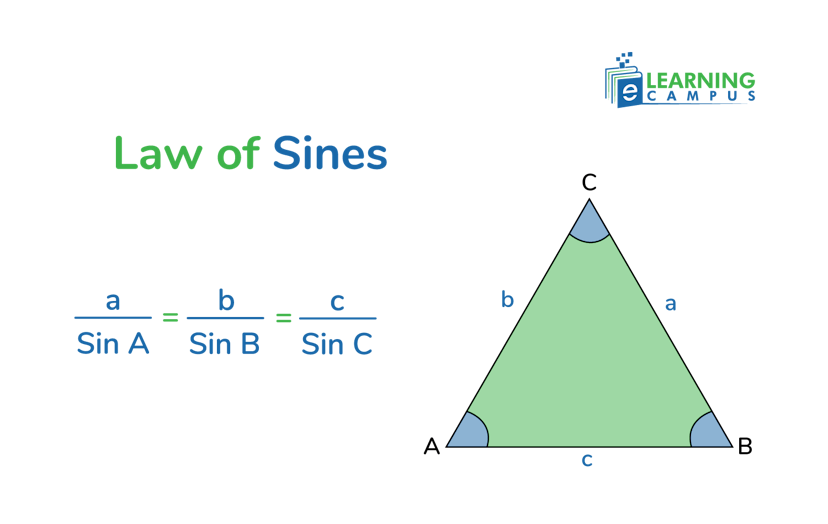
If A, B, and C are the angles of an oblique triangle, and a, b, and c are the lengths of the sides opposite those angles, then the ratio of each side to the sine of its opposite angle is the same.

Mathematically, it is represented as;

asin⁡A=bsin⁡B=csin⁡C\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
 law of sines definition

Proof of Sine Law

The sine law applies to any triangle. However, we need a right triangle to prove this law.  

Let us consider two oblique triangles ABC with altitude h.

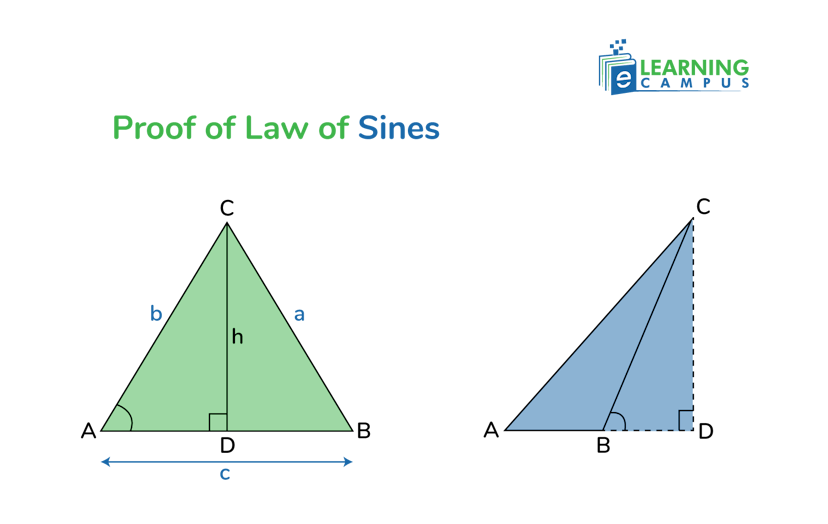
Law of sine proof

For the first triangle, 

sin⁡A=hb\sin A = \frac{h}{b}
h=bsin⁡A(i)h = b \sin A \quad \text{(i)}
Also, \text{Also, }
sin⁡B=ha\sin B = \frac{h}{a}
h=asin⁡B(ii)h = a \sin B \quad \text{(ii)}

Comparing equations (i) and (ii).

If ‘h’ is equalized from both equations. We will get,

asin⁡B=bsin⁡Aa \sin B = b \sin A
asin⁡A=bsin⁡B\frac{a}{\sin A} = \frac{b}{\sin B}

In the same way, we can also find the relation for sin A and sin C. 

asin⁡C=csin⁡Aa \sin C = c \sin A
asin⁡A=csin⁡C\frac{a}{\sin A} = \frac{c}{\sin C}

Combining the above-proved equations, we have,

asin⁡A=bsin⁡B=csin⁡C\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}

Hence, we prove the law of sines.

Application of the Rule of Sines

The sine rule has various applications in trigonometry, including solving triangle-related problems. It is useful in;

  • Finding the triangle’s side length using the ASA or AAS criteria.
  • Calculating the unknown angle of a triangle.
  • Find the area of a triangle.

When to Use the Sin Rule

There are certain conditions to use the sine law. We can use it when we know:

  • Two angles of a triangle and the side opposite one of them, fulfilling the ASA law of sines
  • Two sides of the triangle and the angle opposite one of them, fulfilling the law of sines SSA. 

Finding the Sides and Angle of Triangle Using Sine Law

With the help of the sine rule, we can easily find the missing sides or angles of a triangle if we are given some sort of information about the sides and angles. Let’s look at some of the examples of law of sines problems. 

How to find an angle with two sides

We can find angle from two sides of a triangle by using the formula. Let’s look at the example. 

Consider a triangle with the sides a = 20 cm, c = 25 cm, and Angle C = 40º. Calculate the angle A.  

Solution

According to the given data, we can use the formula,

asin⁡A=bsin⁡B=csin⁡C\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}

For the given condition, we can write it as;

asin⁡A=csin⁡C\frac{a}{\sin A} = \frac{c}{\sin C}

We have to find the angle, so we will rewrite the equation as;

sin⁡Aa=sin⁡Cc\frac{\sin A}{a} = \frac{\sin C}{c}
sin⁡A20=sin⁡40∘c\frac{\sin A}{20} = \frac{\sin 40^\circ}{c}
sin⁡A=sin⁡40∘25×20\sin A = \frac{\sin 40^\circ}{25} \times 20
sin⁡A=0.642825×20\sin A = \frac{0.6428}{25} \times 20
sin⁡A=0.64285×4\sin A = \frac{0.6428}{5} \times 4
sin⁡A=0.51424\sin A = 0.51424
A=sin⁡−1(0.51424)A = \sin^{-1}(0.51424)
A=30.94∘A = 30.94^\circ

How to find sides of a triangle using angles

It is easy to find the sides of the triangle if two of its angles are given. Let's look at the example of how to find side length of triangle with angles. 

Let us consider a triangle with the side a = 6 cm, ∠A = 60°, ∠B = 45°. Find the value of side b.

Solution 

We know that;

asin⁡A=bsin⁡B\frac{a}{\sin A} = \frac{b}{\sin B}
6sin⁡60∘=bsin⁡45∘\frac{6}{\sin 60^\circ} = \frac{b}{\sin 45^\circ}
632=b2\frac{6}{\frac{\sqrt{3}}{2}} = \frac{b}{\sqrt{2}}
123=b2\frac{12}{\sqrt{3}} = b \sqrt{2}
b=1232b = \frac{12}{\sqrt{3}\sqrt{2}}
b=126b = \frac{12}{\sqrt{6}}

So, we solved the SAA triangle with the help of the sine rule. 

Law of Sines Worksheet PDF

Worksheet on law of sines are interactive tools to help you understand, practice, and solve the sine rule problems. We provide you with the law of sines worksheet PDF. You can download the printable PDF worksheet. 

Download PDF

Conclusion

The law of sines is used to find unknown angles or sides of triangles when two angles and one side, or two sides and one angle, are known.  It is the property of a triangle that states that the ratio of each angle and its sides is equal.

Master the Mathematical Skills With Us

Are you struggling with math and want to learn it simply? We can help you. We have expert online Math tutors to teach you math according to your learning pace and requirements. You will get personalized instruction from professionals. 

Math tutor online
Hire a Tutor Now

FAQs