elearning BlogLaw of Cosines

Law of Cosines

law of cosines

The law of cosines is a fundamental relationship in trigonometry that connects the lengths of the sides of any triangle to the cosine of one of its angles. It helps to find the length of unknown sides or angles of a triangle when certain information is given, such as two sides and the included angle, or all three sides. 

What is the Law of Cosines

The law of cosines, also known as the cosine rule, highlights the relationship between the angle and the three sides of the triangle. It states that;

“The square of any one side of a triangle is equal to the difference between the sum of the other two sides’ squares and twice their product and the cosine angle between them.”  

For example, in the triangle ABC given below, with the sides of length a,b, and c, the cosine rule is given as;

a2=b2+c2–2bc.cosAa^2 = b^2 + c^2 – 2bc .cos A

It means that if two sides (b and c) and a corresponding angle (cos A) of a triangle (SAS triangle) are given, we can find the length of the third side (a) of the triangle. 

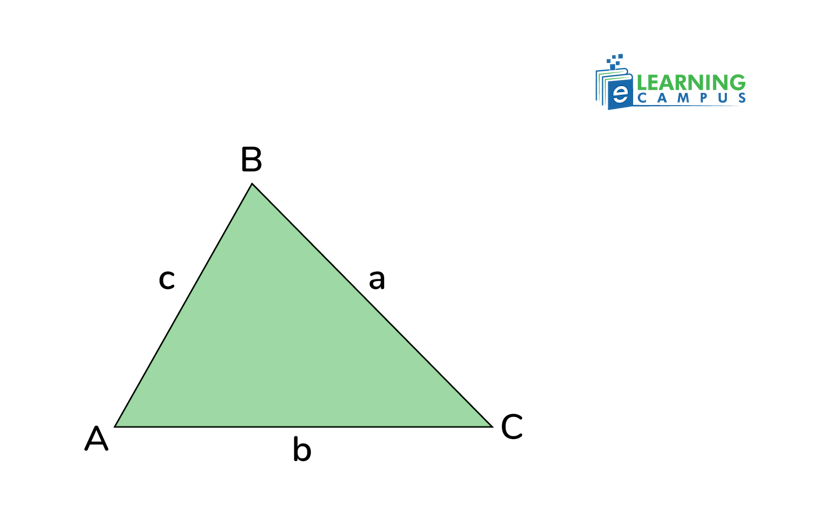
law of cosines example

Cosine Law Formula 

The cosine law formulas are the formulas used to find the missing sides or angles of a triangle, provided that the lengths and angles of the other sides are given. We will understand it with the help of an example.

Let’s consider a triangle ABC with the sides a, b, c, and corresponding angles , , as shown below. 

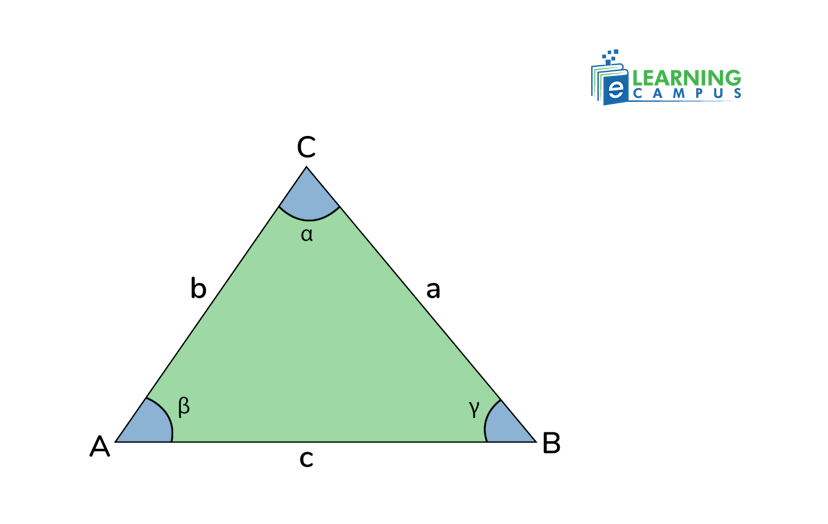
Law of cosines formula

Based on the above triangle, the formulas to find the length of the sides of the triangle are given as;

a2=b2+c2–2bccosαa^2 = b^2 + c^2 – 2bc cos α
b2=a2+c2–2accosβb^2 = a^2 + c^2 – 2ac cos β
c2=b2+a2–2bacosγc^2 = b^2 + a^2 – 2ba cos γ

In the same way, we can find the missing angles if the three sides of a triangle are given. The formula to find each angle is given as;

cos⁡α=b2+c2−a22bc\cos \alpha = \frac{b^2 + c^2 - a^2}{2bc}
cos⁡β=a2+c2−b22ac\cos \beta = \frac{a^2 + c^2 - b^2}{2ac}
cos⁡γ=b2+a2−c22ab\cos \gamma = \frac{b^2 + a^2 - c^2}{2ab}

So, by using the above formulas, we can find the unknown sides and angles of the triangle.  

Proving the Law of Cosines

The cosine rule can be proved in many ways. We will prove it with the help of trigonometry. 

Let’s consider a triangle ΔABC. It is a non-right triangle (oblique). 

In triangle ABD,

sin⁡A=hc\sin A = \frac{h}{c}
h=csinA……(i)h=c sinA……(i)
cos⁡A=rc\cos A = \frac{r}{c}
r=ccosA………(ii)r=c cos A……… (ii)

We will apply Pythagoras' theorem in ΔCBD. So we have,

a2=h2+(b−r)2a^2 = h^2 + (b - r)^2

Substitute the values of h and r from equations (i) and (ii). 

a2=h2+(b−r)2a^2 = h^2 + (b - r)^2
a2=(csin⁡A)2+(b−ccos⁡A)2a^2 = (c \sin A)^2 + (b - c \cos A)^2
a2=c2sin⁡2A+b2−2bccos⁡A+c2cos⁡2Aa^2 = c^2 \sin^2 A + b^2 - 2bc \cos A + c^2 \cos^2 A
a2=c2(sin⁡2A+cos⁡2A)+b2−2bccos⁡Aa^2 = c^2 (\sin^2 A + \cos^2 A) + b^2 - 2bc \cos A
a2=c2(1)+b2−2bccos⁡Aa^2 = c^2(1) + b^2 - 2bc \cos A
a2=c2+b2−2bccos⁡Aa^2 = c^2 + b^2 - 2bc \cos A

Hence, the cosine law is proved using Pythagoras' theorem. 

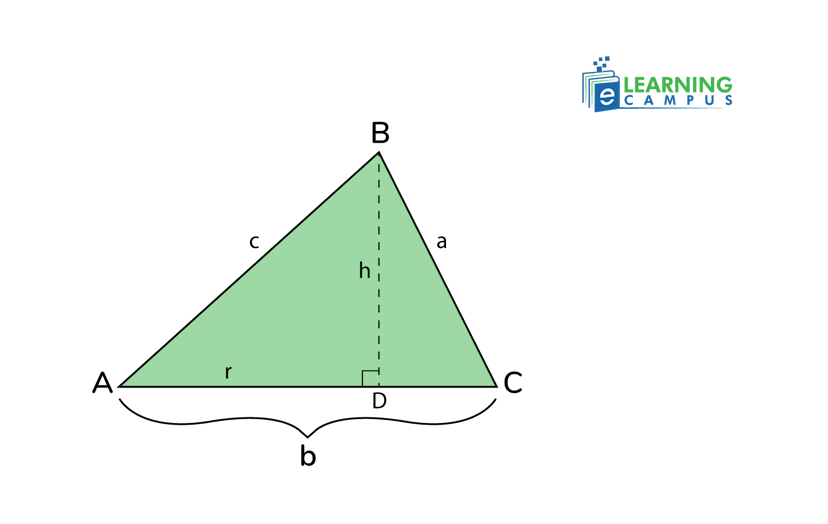
Law of cosines proof

The other side can also be found using this method. 

Finding the Length and Angle Using the Cosine Rule

Using the cosine rule, we can easily find the missing angle and the length of the side of the triangle. Let’s look at some examples of solving law of cosines problems. 

How to Find an Angle With 3 Sides

First, we will find an angle given 3 sides. Let’s consider a triangle with the sides 4 cm, 6cm, and 8 cm. Find the measure of angle A.

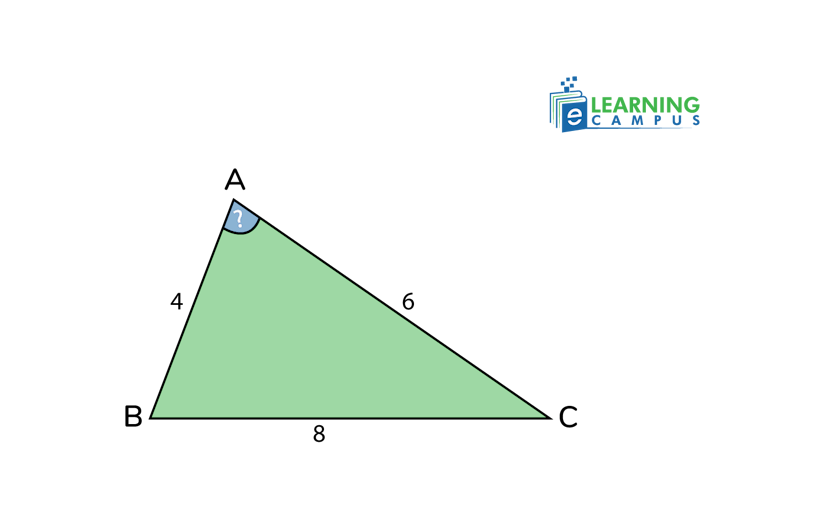
Find an angle given 3 sides

To find the angle of a triangle with the given 3 sides, we will use the formula.

a2=b2+c2−2bc.cosAa^2 = b^2 + c^2 - 2bc.cosA

Putting the values in the formula.

82=62+42−2(6)(4)cos⁡A8^2 = 6^2 + 4^2 - 2(6)(4) \cos A
64=36+16−48cosA64=36+16-48 cosA
64=52−48cosA64=52-48 cosA
48cosA=52−6448 cosA= 52-64
48cosA=−1248 cosA=-12
cos⁡A=−1248\cos A = \frac{-12}{48}
A=cos−1248A=cos \frac{-12}{48}
A=104.5°A=104.5°

How to Find Side With Angle and Sides

Now we will learn how to find Side with Angle and Sides. Let us consider a triangle whose two sides and one angle are given (SAS triangle). 

Consider a triangle XYZ with two sides of 6 cm and 9 cm, and an angle between them is 131 degrees as shown below. Find the length of the missing sides. 

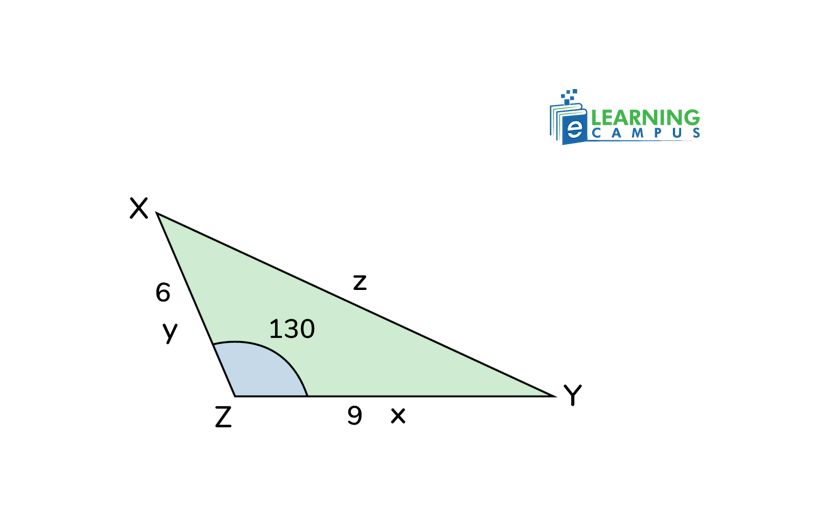
law of cosines SAS.

To find the missing side, we will use the law of cosines SAS. 

z2=x2+y2−2xycosZz^2 = x^2 + y^2 − 2xy cosZ
z2=92+62−2(9)(6)cos(131)z2 = 9^{2} + 6^{2} − 2(9)(6) cos(131)
z2=81+36−108(−0.656)z^2 = 81 + 36 − 108 (−0.656)
z2=117+70.848z^2 = 117 +70.848
z2=187.848z^2 =187.848
z=187.848z = \sqrt{187.848}
z=13.7z=13.7

 Law of Cosines and Pythagoras' Theorem 

The Pythagorean theorem is a special case of the law of cosines. The cosine law is applied to all types of triangles, while Pythagoras' theorem is only applicable to the right triangle. 

The Pythagorean theorem is a² = b² + c² and the cosine rule is a² = b² + c² - 2bc cos A. 

When the angle in the cosine rule is a right angle (90 degrees), the cosine of that angle is 0. This causes the term "- 2bc cos A" in the law of cosines to disappear, leaving only a² = b² + c², which is the Pythagorean theorem. 

Let’s look at the proof.

The cosine law is expressed as;

a2=b2+c2−2bc(cosA)a² = b² + c² - 2bc (cos A)

When the angle is 90, then, 

a2=b2+c2−2bc(cos90)a² = b² + c² - 2bc (cos 90)
a2=b2+c2−2bc(0)a² = b² + c² - 2bc (0)
a2=b2+c2−0a² = b² + c² -0
a2=b2+c2,a² = b² + c²,

which is Pythagoras’ theorem.

Hence,  proved that the Pythagorean theorem is a special case of the cosine law.  

Conclusion 

The law of cosines relates the relation between the length of sides of any triangle the the measurement of its angle. It is usefu to find the missing sides or angles of a triangle when specific sides and angles are known. The Pythagorean theorem is a special case of the cosine rule. 

Learn Math with live tutors 

Are your kids struggling with Math? Don’t worry. We have a solution for you. We have expert online math tutors who make math fun for students. You will get personalized live classes and overcome your grey areas.

Online math tutor
Hire a Tutor Now   

FAQs