How to Factor a Quartic Polynomial

Are you struggling to find the roots of a complex expression where the highest exponent is four? Students usually find factoring quartic polynomials challenging. It involves finding roots, testing them with synthetic division or substitution to find linear factors, and then factoring the remaining quadratic or cubic expression. 

In this blog, you will learn the methods for factoring quartic polynomials, including grouping, synthetic division, and identifying special patterns like the quadratic form.  

What is a Quartic Polynomial 

A quartic polynomial is a polynomial of the fourth degree. It is a polynomial in which the highest exponent of the variable is 4. 

The standard form of a quartic polynomial is written as:

Where a, b, c, d, e are constant known as coefficients and a≠0. 

Learn Math online with expert tutors 

Factorizing Quartic Polynomials

The factorization of quartic polynomials involves several methods. It ranges from special cases to general algorithms. The primary methods include finding roots via the Rational Root Theorem and synthetic division, factoring by grouping, using the difference of squares, substituting u = x²

(for quadratic forms), and applying Ferrari's method or factoring into two quadratics. 

You will learn the factorization of quartic polynomials using different methods.

Factoring by Grouping 

Factoring a quartic polynomial by grouping is a technique where we arrange terms into groups that share common factors, then factor out those common elements.

This method works with polynomials with 4 terms.

Example:

Factorize

First, we will group the terms in pairs

Then, factor out the GCF from each group

Now, notice the common binomial factor

So, the factors are

Rational Root Theorem

The Rational Root Theorem helps find rational roots (solutions) of polynomial equations, which then helps us factor the polynomial. 

The Theorem Statement states that;

If a polynomial equation has integer coefficients:
aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀ = 0

Then any rational root p/q (in lowest terms) must satisfy:

• p divides a₀ (the constant term)
• q divides aₙ (the leading coefficient)

In simpler terms, Possible rational roots = ± (factors of constant term)/(factors of leading coefficient)
Example 

Factor x⁴ + 2x³ - 7x² - 8x + 12 = 0

Identify the coefficients

• Leading coefficient = 1
• Constant term = 12

List the factors of the coefficients

• Factors of 12: ±1, ±2, ±3, ±4, ±6, ±12
• Factors of 1: ±1

The possible rational roots are 

±1, ±2, ±3, ±4, ±6, ±12

Substitute the value and test systematically.  If 𝑓(𝑘)=0, then (𝑥−𝑘) is a factor.

Testing x = 1:
x⁴ + 2x³ - 7x² - 8x + 12 = 0

1⁴ + 2(1)³ - 7(1)² - 8(1) + 12 = 0

1 + 2 - 7 - 8 + 12 = 0 

𝑓(1)=0

So, (𝑥−1) is a factor

Use Synthetic Division or long division to divide the quartic by the factor. 

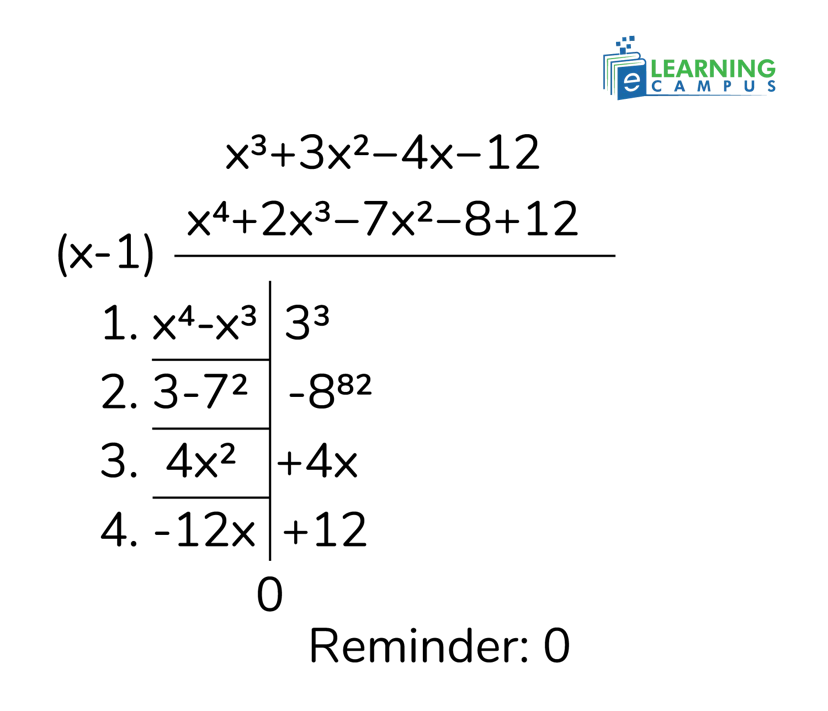
Result: x³ + 3x² - 4x - 12. This is a cubic polynomial. 

Now, find the roots of the cubic

Testing x = -2 in x³ + 3x² - 4x - 12

(-2)³ + 3(-2)² - 4(-2) - 12

-8 + 12 + 8 - 12=0

So, x-2 is the factor. 

Synthetic division by (x + 2)

Result: x² + x - 6

Now, factor this quadratic equation

x² + x - 6 

(x + 3)(x - 2)

So, the final factors are (x - 1)(x + 2)(x + 3)(x - 2)

Substitution (Biquadratic Form) 

Substitution is a method for factoring certain quartic polynomials by temporarily converting them into quadratic form, which is much easier to factor.

A biquadratic polynomial has only even powers of x. Its general form is given as: 

ax⁴ + bx² + c

For example, x⁴ - 5x² + 4, 2x⁴ + 7x² - 15. There are no x³ or x terms and no odd powers in the expression. 

The Substitution Method

Since x⁴ = (x²)², we can substitute u = x² to convert the quartic into a quadratic.

So, x⁴ + bx² + c becomes u² + bu + c

Then we:

• Factor the quadratic in u
• Substitute x² back for u
• Factor further using the difference of squares

Example

Factor x⁴ - 5x² + 4

First, substitute u = x²

x⁴ - 5x² + 4

(x²)² - 5(x²) + 4

u² - 5u + 4

Now, factor the quadratic

Find two numbers that multiply to 4 and add to -5:

So, the numbers are -4 and -1. Then, 

u² - 5u + 4 = (u - 4)(u - 1)

Substitute x² back for u

(u - 4)(u - 1)

(x² - 4)(x² - 1)

Factor further (difference of squares)

x² - 4 = (x - 2)(x + 2)

x² - 1 = (x - 1)(x + 1)

So, the factors are (x - 2)(x + 2)(x - 1)(x + 1)

Verification: Roots are x = 2, -2, 1, -1

Completing the Square 

Completing the square is an algebraic technique that transforms expressions into perfect square form. For quartics, it is used to factor polynomials that don't yield to simpler methods.

In a perfect square, the constant term is the square of half the coefficient of x.

Completing the Square for Quadratics

Example: x² + 6x + 5

We have to write as (x + a)² + b. For this, we follow these steps.

Take half of the x coefficient: 

62= 3

Square it.

3² = 9

Add and subtract this value:

x² + 6x + 9 - 9 + 5

(x² + 6x + 9) - 4

Factor the perfect square:

(x + 3)² - 4

Factor using the difference of squares. 

(x + 3)² - 2²

[(x + 3) - 2][(x + 3) + 2]

(x + 1)(x + 5)

So, the factors are (x+1) (x+5). 

Factoring Quartic Polynomials Worksheet

A Factoring Quartic Polynomials Worksheet is an educational resource designed to help students practice breaking down fourth-degree polynomials into smaller, simpler factors. These worksheets typically cover several specific factoring methods tailored to the structure of the quartic equation. 

We provide you with a free printable worksheet on factoring quartic polynomials. 

Conclusion

Factoring a quartic polynomial

involves reducing it to lower-degree polynomials, typically quadratics, through methods like grouping, finding rational roots, or factoring as a quadratic form

Key techniques include the rational root theorem, synthetic division, or splitting middle terms.