elearning BlogCompleting the Square Worksheet

Completing the Square Worksheet

Quadratic equations using completing the square worksheets

Quadratic equations can be solved by many methods. Completing the square is a method of solving quadratic equations when they can’t be factorized. In this blog, you will learn how to solve quadratic equations with the help of completing the square worksheets. 

Completing the Square Method 

Completing the square is the process of solving quadratic equations by converting them into a perfect square form. Most of the quadratic equations in algebra can not be written in perfect square form, therefore, this method is taken into account to solve them.  

We know that the quadratic equation in the standard form a

ax2+bx+c=0ax^2 + bx + c = 0

is easy to solve by factorization. But, sometimes we can not factorize it. In this case, we can use completing the square method to solve the problem.

Let’s look at completing the square example to understand it thoroughly.  

Example: 

We have

x2+2x+3x^2 + 2x + 3

which can not be factorized. However, it can be converted to

(x+m)2(x + m)^2

by completing the square method. Where

(x+m)2(x + m)^2

is the perfect square.  

Completing the Square Formula 

Completing the square is an algebraic expression that helps to convert the quadratic expression into a perfect square form. 

The general formula for completing the square is;

ax2+bx+c⇒a(x+m)2+nax^2 + bx + c \Rightarrow a(x + m)^2 + n

Where m is found by

b2a\frac{b}{2a}

and n is found by

c−b24ac - \frac{b^2}{4a}
  • To find the perfect square, the coefficient of x should be equal to 1. Therefore, a is taken as a common factor to make it 1.

Steps of Completing the Square Method 

To convert any equation into a perfect square and solve the quadratic equations, follow these steps. 

1.Write the equation in the standard form

x2+bx+cx^2 + bx + c

2.The coefficient of

x2x^2

should be equal to 1. If it is not 1, make it by taking the coefficient of

x2x^2

as a common factor. 

3.Find the half of the coefficient of x.

4.Take the square of half of the coefficient of x.

5.Add and subtract the squared number after x term. 

6.Factorize the equation. 

We will understand solving quadratic equations by completing the square method with an example. 

Example: 

Complete the square in a quadratic expression

6x2−12x−86x^2 - 12x - 8

We will follow the steps.

  • We make the coefficient of
x2x^2

equal to 1. So, we will take 6 as a common factor.

  • The equation will become
6(x2−2x−8)6(x^2 - 2x - 8)
  • Calculate the half of the coefficient of
x i.e.22=1x \ i.e. \frac{2}{2} = 1

so, the coefficient of x becomes 1. 

  • Find the square of the coefficient
x⋅12=1x \cdot 1^2 = 1
  • Add and subtract the square of the coefficient of x after x. 
  • So, the equation
6(x2−2x−8)6(x^2 - 2x - 8)

will become

6(x2−2x+1−1−8)6(x^2 - 2x + 1 - 1 - 8)
  • Using the identity
x2+2xy+y2=(x+y)2x^2 + 2xy + y^2 = (x + y)^2

write the first three terms in the perfect square form. The equation becomes

x2+2x+1=(x+1)2x^2 + 2x + 1 = (x + 1)^2
6(x+1)2−1−86(x + 1)^2 - 1 - 8
  • Now, simplify -1-8.
6(x+1)2−96(x + 1)^2 - 9

Thus, we completed the square.

6x2−12x−8=6(x+1)2−96x^2 - 12x - 8 = 6(x + 1)^2 - 9

In this equation,

(x+1)2(x + 1)^2

is the perfect square.

Completing the Square Shortcut Method 

In the shortcut method of completing the square, we find the closest perfect square of the expression and expand it. Then compare the expanded expression with the original expression. Then we add or subtract values accordingly.

Let’s understand it with the help of an example completing the square.

Example: 

Complete the square of the given expression

x2+10x+15x^2 + 10x + 15
  • Divide the coefficient of x by 2.
102=5\frac{10}{2} = 5
  • Find the closest perfect square which is equal to
∣(x+5)2∣\left| (x + 5)^2 \right|
(x+5)2=x2+2(x)(5)+52=x2+10x+25(x + 5)^2 = x^2 + 2(x)(5) + 5^2 = x^2 + 10x + 25
  1. Now compare the constant with the original constant value. 
  • The original constant is 15 and the constant of the closest perfect square is 25. So, we will subtract 10 to the expression.
  • So, the perfect square form is
(x+5)2−10(x + 5)^2 - 10

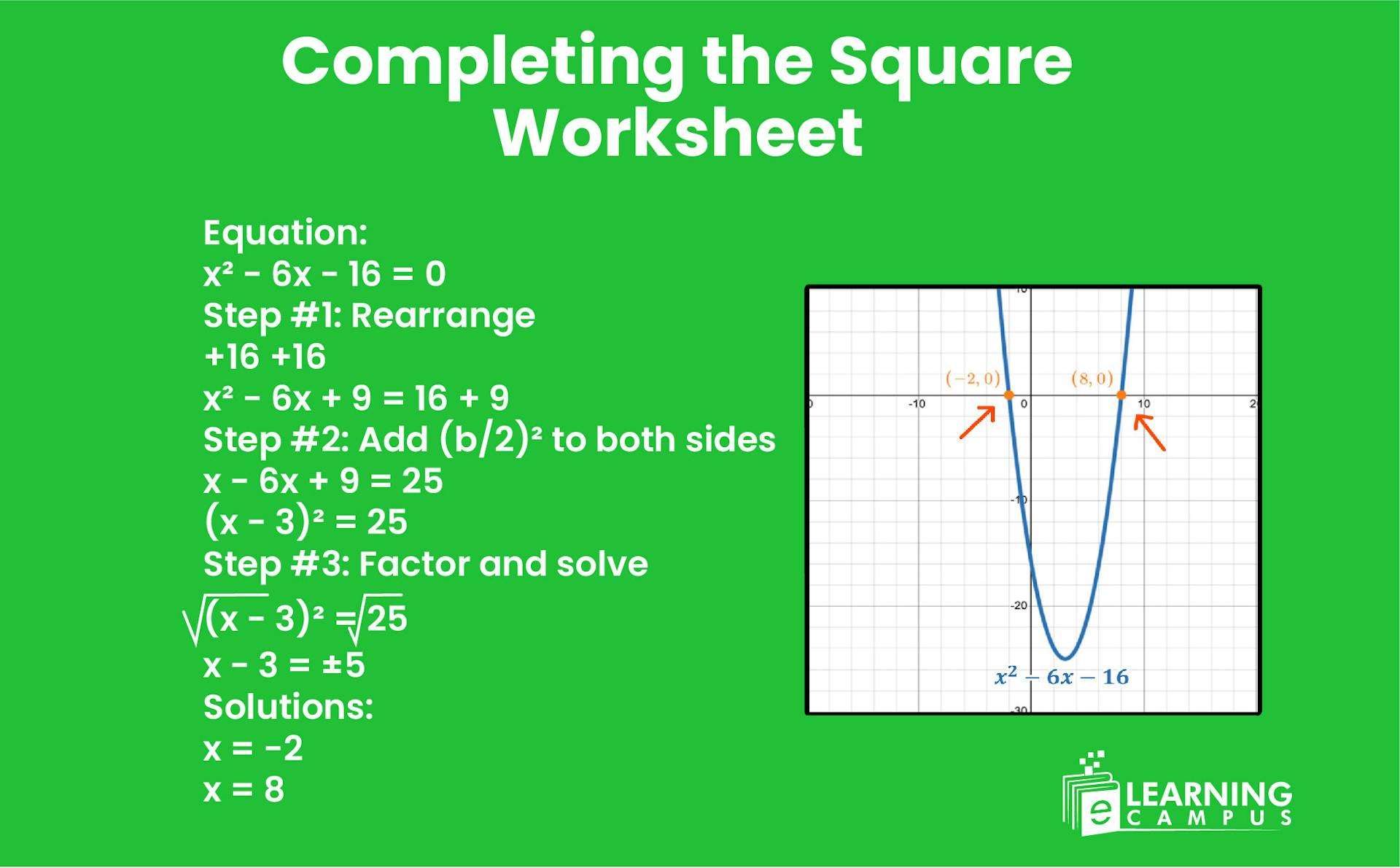
Worksheets on Completing the Square

As of now we learned methods of completing the square. Here, we provide you with the worksheets on completing the square to help you practice the questions. Solve each question using different methods and enhance your mathematical skills. 

Solve quadratic equation using worksheets on completing the square

Learn Math With Professional Tutors

Are you searching for an online math tutor to teach your kids? Get our service. We have professional and expert math tutors to make math easy for your kids. 

Hire a Professional math tutor
Hire Tutor Now

FAQs