What is Slope in Math 

Have you ever felt a steepness while pushing your bike up a hill or zooming down a water slide? How do we move in a specific direction in steepness? In Math, this direction and steepness are referred to as slope. 

So, what does slope look like in math? How do we calculate it? And why does it matter? In this blog, we will explain the slope, its types, and its usage in Mathematics. 

Definition of Slope

Slope is a numerical value that describes the steepness and direction of a line. It is the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. 

The slope represents two kinds of changes;

• Rise: The vertical change of something known as the ‘rise’.
• Run: The horizontal change of something known as the ‘run’. 

In practical terms, if a line has a slope of 2, it means that for every 1 unit you move to the right, the line goes up by 2 units. If the slope is -3, then for every 1 unit you move right, the line drops by 3 units.

Also, learn about the Transformation of Functions 

What is the Slope Formula?

The slope formula is the mathematical representation of the rate of change or steepness of a line between two points. The formula calculates the slope by dividing the change in the y-coordinates by the change in the x-coordinates between the two points. The formula is also called rise over run. It is represented by m.  

Mathematically, the formula of slope for two points on a line is written as;

m= (y₂ - y₁)(x₂ - x₁) = Rise Run

Where, 

• m represents the slope of the line (m=Slope).
• (x₁, y₁) shows the coordinates of the first point on the line. 
• (x₂, y₂) represent the coordinates of the second point on the line. 
• Y₂-y₁ is the vertical change between the two points, also known as the rise. 
• x₂-x₁ is the horizontal change between the two points, also known as the run. 

What are the Types of Slope

Slope is a measure of a line’s steepness and direction on a graph. Based on the direction of a line on a graph, the slopes have been categorized into four types. The four types of slopes are positive, negative, zero, and undefined. 

We will discuss the types of slopes in detail. 

Positive Slope 

A positive slope is the upward direction of a line on a graph. It indicates a direct relationship between variables. As the value on the horizontal x-axis increases, the value on the vertical y-axis also increases. The positive slope rises from left to right on the graph. 

Example

The relationship between the number of hours a student studies and the test score will be a positive slope. As the hours studied increase, the test score will also increase. 

If we represent the number of hours on the x-axis and scores on the y-axis, then the slope will be like;

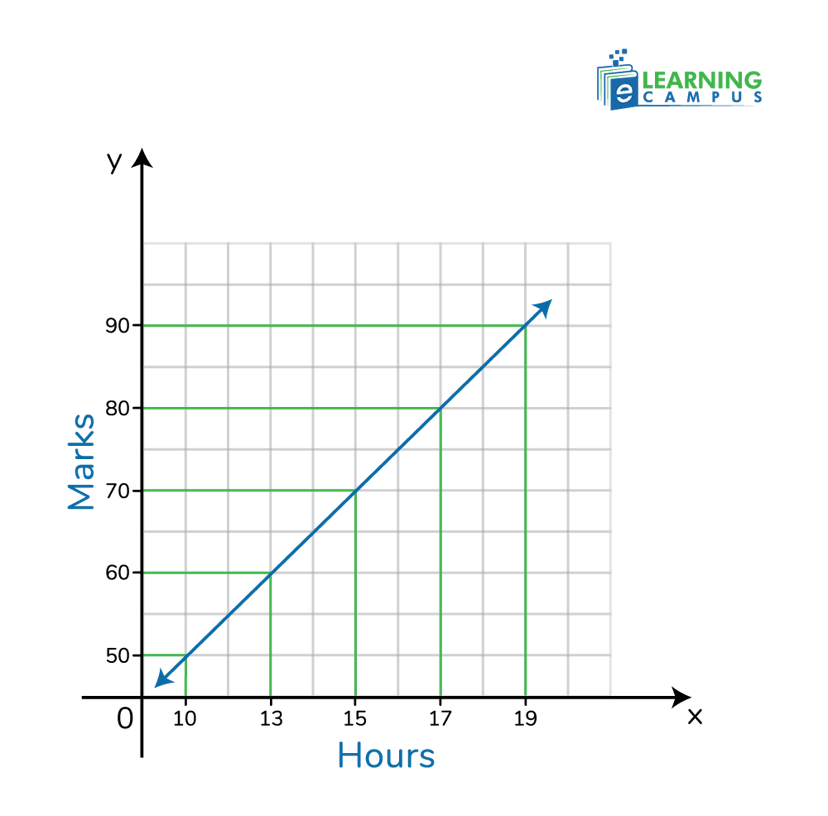
Negative Slope

A negative slope is a line on a graph that moves downward from left to right. This represents an inverse relationship between variables. It shows that the value of one variable corresponds to a decrease in the value of the other.

Negative slopes can be used in many situations where quantities change in opposite directions.

Example: 

In our daily routine, as the price of a product increases, the demand for that product typically decreases.

If we represent the price of the product on the x-axis and demand on the y-axis, the slope will be downward. 

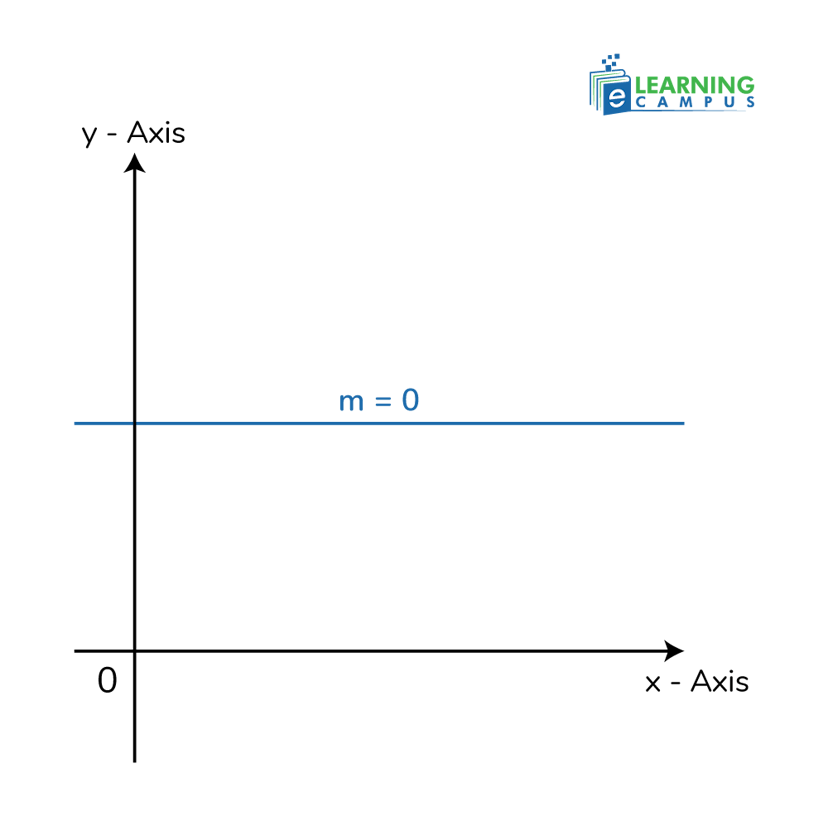
Zero Slope 

A zero slope represents a perfectly horizontal line on a graph. It shows no change in the y-coordinate over any change in the x-coordinate. On a coordinate plane, a horizontal line runs perfectly flat and parallel to the x-axis. 

Undefined Slope 

An undefined slope shows a zero change in the x-axis. In this case, x2-x1 is zero. So, according to the formula, the division by zero is not mathematically defined. Therefore, it is known as an undefined slope. 

The concept of slope is usually asked in college entry tests such as the SAT and GMAT. You can prepare for the SAT and GMAT online with expert tutors. 

How to Find the Slope

The slope of a line can be found from a graph, an equation, or two points by calculating the ratio of the vertical change to the horizontal change (rise over run). 

Finding the Slope of a Line From a Graph

If you have a graph of the line, you can find the slope by counting the rise and run between two points. 

• Identify two clear points on the line, preferably at integer coordinates, to make counting easier.
• Count the rise. Start at the left-most point and count the number of units you move up or down to reach the same vertical level as the second point.
• Count the run. From that new position, count the number of units you move left or right to get to the second point.
• Divide rise by run to find the slope.

Finding the Slope From Two Points

If two points are given, the slope of a line can be found easily by using the 2-point slope formula. For example, to find the slope of a line passing through points (2, 3) and (4, 11), we can use the point-slope formula. 

In this case, x1 is 2, and x2 is 5, y1 is 3, and y2 is 11. 

The formula to find the slope of a line is given as

Calculating the Slope From an Equation

The slope of a line can also be found from an equation. To find it, rearrange the equation into slope-intercept form (y=mx+b) by isolating y on one side of the equation. Then the coefficient of the x term is the slope.  

For example, in the equation y=3x-6, the slope is 3. 

If you are homeschooling, you can learn the concept of slope with online tutors for math. 

How to Calculate the Percentage of a Slope

The percentage of a slope or percent grade tells the amount of vertical elevation change (rise) for every 100 units of horizontal distance (run). It shows how steep a surface is. 

For example, a 6% slope means there is a 6-unit vertical rise over a 100-unit horizontal run.  

The percentage of a slope is found by dividing the vertical rise by the horizontal run and then multiplying the result by 100. 

The formula to calculate the percentage of slope is given as;

For example, if there is a 10-foot vertical rise over a 100-foot horizontal distance, then the slope percentage will be calculated as;

Conclusion 

In mathematics, slope represents the steepness of a line and represents the rate at which the dependent variable (y) changes with respect to the independent variable (x). It is commonly calculated as rise over run. It means the vertical change (rise) divided by the horizontal change (run) between any two points on the line. The slope can be positive, negative, zero, or undefined.