Transformations of Functions

The transformations of functions refer to the fluctuations within a graph. It means altering the graph of a function to create a new graph, such as shifting, reflecting, stretching, or compressing it. In mathematics, there are four types of function transformations, namely translation, reflection, rotation dilation. 

What are Function Transformations 

In mathematics, a function is a relationship between inputs, in which each input is related to one output. The definition of transformation in math is a change in the position or size of anything. So, in mathematical terms, the function transformation is the change in the shape or size of the graph of a function.   

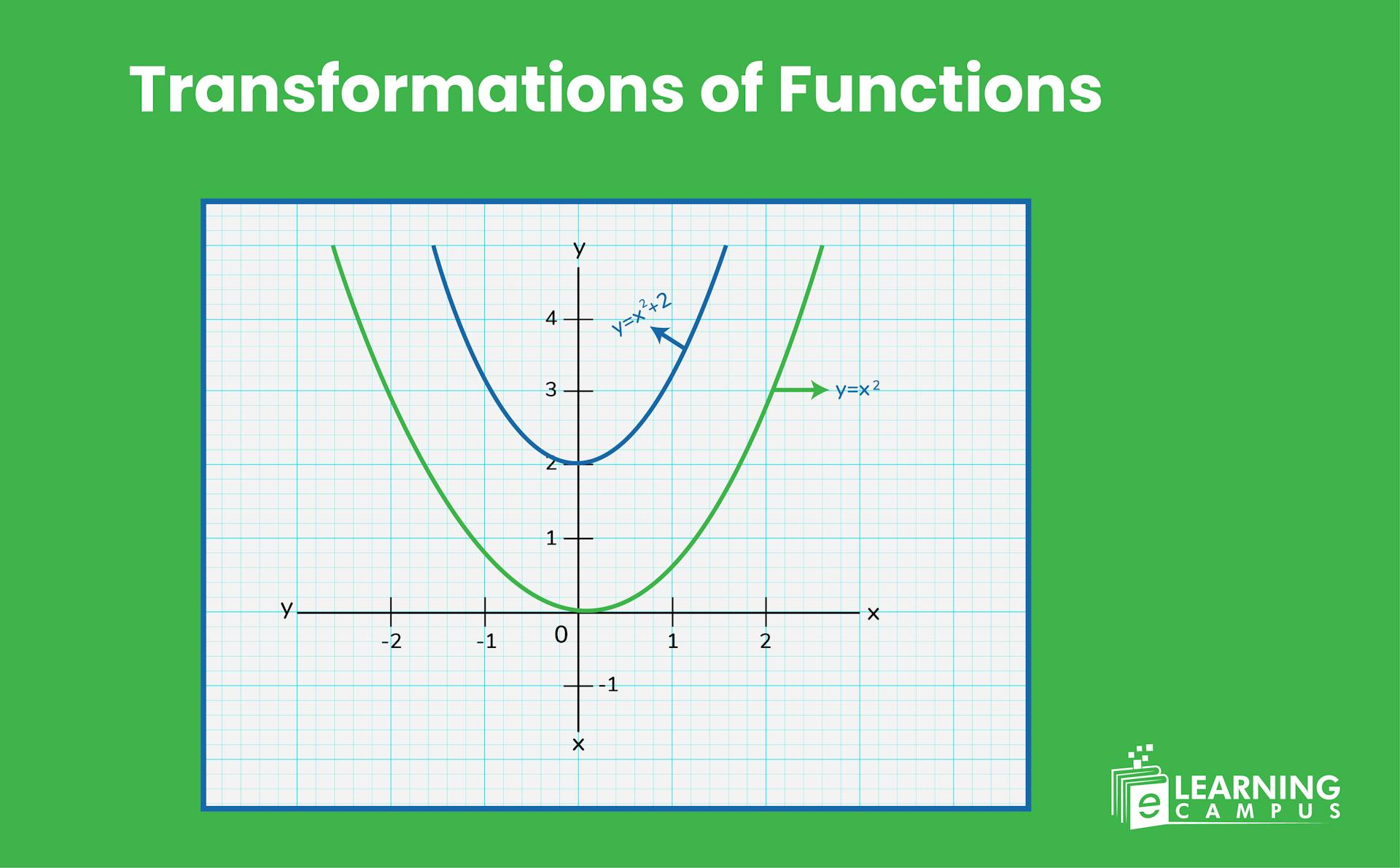
A simple example of a function transformation is shifting the graph of a function up or down. 

For instance, we have the function

 If we add 2 to it, a new function will form, which will be represented as;

Which is the graph of f(x) moved up by 2 units. 

Types of Transformations of Functions

The function transformations modify the graph of a function, changing its position, size, or orientation. There are four types of transformations of functions that change the graph in one way or another. We will discuss them in detail. 

Translation 

Translation of a function is a shift in the graph of the function without changing its shape or size. It occurs when every point of a function on a graph moves by the same amount in the same direction. Translation can either be vertical or horizontal. 

Vertical Translation

In a vertical translation of a function, the graph of a function slides either upward or downward. This translation is generally expressed as;

If a function moves upward.

If a function moves downward

In the above expressions, ‘k’ is the distance a function moves upward or downward. 

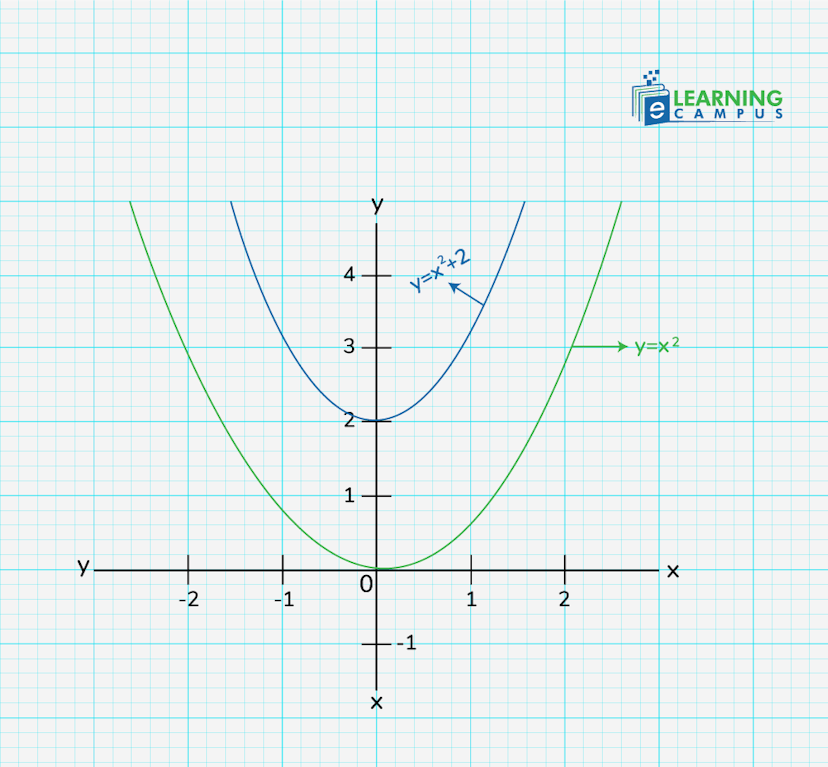
Let’s see an example of a function’s vertical translation. 

Suppose we have a function

The blue line in the first diagram shows the original position of a function. The green line shows the upward movement of the function. This is the vertical translation of the function y=f(x). The function has translated up two steps, so it will be expressed as;

In the second diagram, the red line shows the downward translation of the function. As the function has slid 2 units downward, the function y=f(x) will be expressed as;

Horizontal Translation

In a horizontal translation, a function either moves the left side or the right side. The general form of a function is expressed as;

If the function moves to the right side from the center, it will be written as;

Where ‘k’ shows the distance a function has moved. 

If the function moves to the left side from the center, it will be written as;

Let’s look at the example. 

Consider we have a function  y=f(x)

The blue line in the diagram below shows the original position of the function. The green line shows the horizontal translation of the function. As the function has moved two steps to the right side, it will be expressed as;

The red line in the second image shows that the function has moved two steps leftward. It will be expressed as;

Dilations of Functions

The dilations of functions refer to either stretching or shrinking a graph along the x-axis and the y-axis. Dilation of a function changes the shape of the graph by stretching or shrinking it in one direction. 

If the dilation occurs along the x-axis, all the values on the x-axis will increase. The same change will occur along the y-axis. 

Dilation is divided into two ways. 

Vertical Dilation

Vertical dilation, also known as vertical shrink or stretching, is a transformation that changes the vertical scale of a function's graph. When the function is multiplied by a scale factor 'k', the graph stretches vertically.

• If k > 1, then the graph stretches. It means if the constant ‘k’ is greater than 1, the graph will stretch.
• If 0 < k < 1, then the graph shrinks. It means if the constant ‘k’ is a number between 0 and 1, the graph will be narrower or shrink. 

In vertical dilation, the x- x-coordinates remain the same, and the change occurs in y-coordinates.

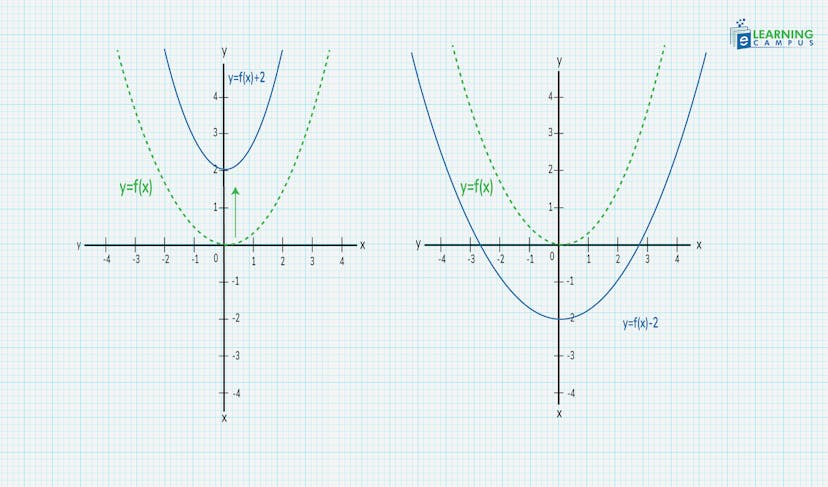
Let’s look at the example.

Suppose we have a function

The green curve shows the original position of the function

If the

is multiplied by a constant greater than 1, for example, 2, 

the graph will shrink horizontally as shown in blue.

If the x2 is multiplied by a constant between 0 and 1, for example, 0.5, 

the graph will stretch horizontally as shown in black.

Horizontal Dilation

A Horizontal dilation, also known as horizontal shrink or horizontal stretching, transforms a function by changing its width. It is achieved by multiplying the x-coordinates of the function's points by a scale factor 1/k. 

• If k > 1, then the graph shrinks. It means if the constant ‘k’ is greater that 1 the graph will shrink horizontally.
• If 0 < k < 1, then the graph stretches. It means if the constant ‘k’ is a number between 0 and 1, the graph will be wider, or stretched horizontally.

In horizontal dilation, y-coordinates remain the same, the change occurs only in x-coordinates. 

Let’s look at the example of horizontal stretch.

Suppose we have a function

The green curve shows the original position of the function

If the

is multiplied by a constant 1/3, then,

the graph will shrink horizontally as shown in blue.

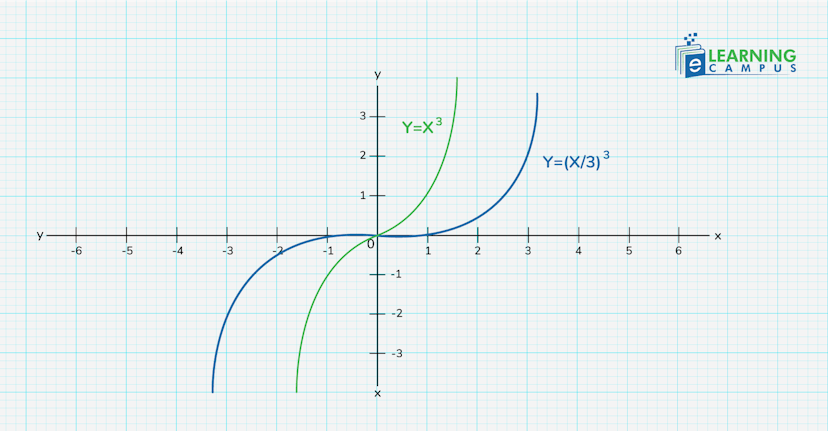
Reflection of Function 

A reflection in the function's transformation is the mirror image of the curve with respect to either the x-axis or the y-axis. This occurs when the function is multiplied by a minus sign. 

Vertical Reflection 

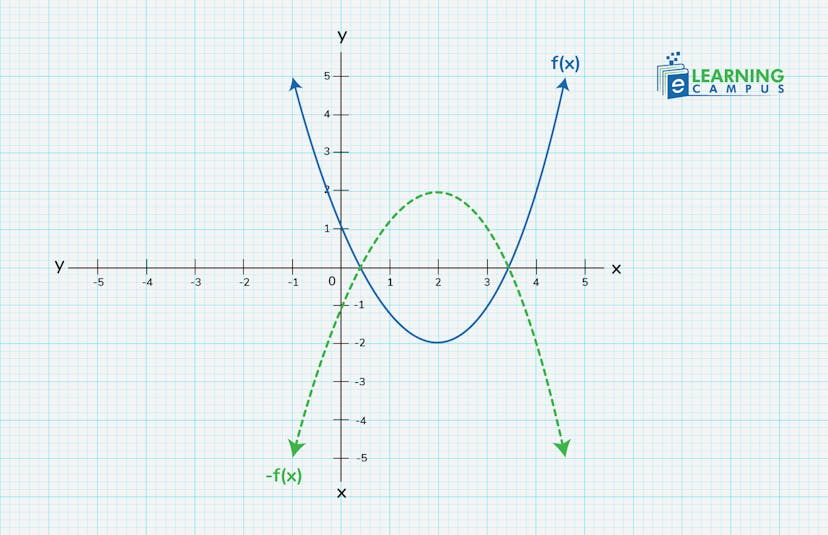
A vertical reflection of a function is a mirror image of the function across the x-axis. This means that the y-values of the original function are negated, while the x-values remain the same. 

• If  y = f(x) with respect to the x-axis, then y = - f(x) will be the reflection.

In the below graph, the blue curve shows the function y = f(x) and the green curve shows the reflection of y = f(x), that is y = - f(x).

Horizontal Reflection 

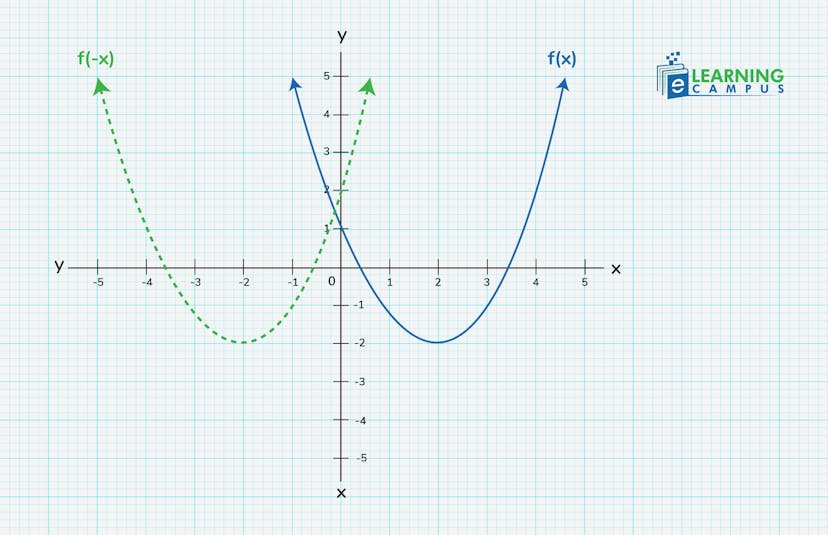
The horizontal reflection is a transformation that creates a mirror image of a graph along the y-axis.

• If y = f(x) with respect to the y-axis, then y = f(-x) will be the reflection.

Rotation of Functions 

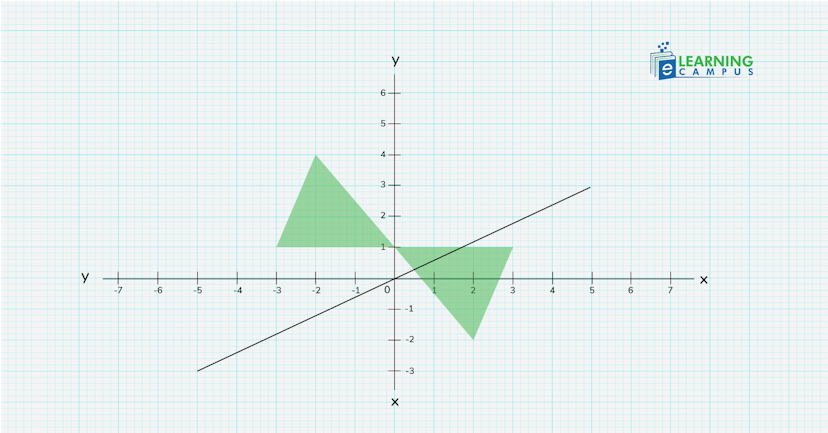
Rotation of Functions refers to a transformation that rotates the graph of a function around a fixed point, typically the origin, by a certain angle. 

The general rule of rotation of a function about the origin is given as;

• To rotate 90º,  (x,y) → (-y, x)
• To rotate 180º,  (x,y) → (-x,-y)
• To rotate 270º,  (x,y) → (y, -x)

Conclusion 

The transformations of functions involve changing the position, shape, or size of the graph of a function. These changes can be achieved through shifts, reflections, stretches, or compressions. The common transformations are dilations, translations, rotations, and reflections.