Corresponding Angles

Are you confused about the corresponding angles and don’t know how they form? This is a common issue for students. Corresponding angles form when a transversal line intersects two other lines that create two angles in the same relative position at each intersection. 

If you are struggling to understand which angles are corresponding angles and what their properties are, this blog will help you in this regard. 

What are Corresponding Angles

Corresponding angles are pairs of angles that are formed when a transversal line intersects two other lines. These lines are located in the same relative position at each intersection. 

If the transversal line intersects parallel lines, then these corresponding angles are always congruent (equal in measure).  

• A transversal is a line that intersects two or more other lines at distinct points. 

Corresponding refers to two things that are connected or line up in some way. In geometry, corresponding angles are defined as a pair of angles that are in the same position relative to each other at each intersection when a transversal line cuts across two other lines.

Types of Corresponding Angles

The intersection of a transversal line and two other lines makes corresponding angles. There are two types of corresponding angles based on whether a transversal intersects parallel or non-parallel lines.

Meet the top-rated online Math Tutors. 

Corresponding Angles with Parallel Lines

When a transversal intersects two parallel lines, it creates pairs of corresponding angles that are congruent. It means they have the same measure. Corresponding angles are found in matching positions relative to the parallel lines and the transversal. For example, both angles above the parallel lines on the same side of the transversal, or both below, or both to the left or right.

Example: 

Two parallel train tracks crossed by a diagonal path (the transversal). If the angle where the path meets the top track on the left side measures 70°, the corresponding angle where the path meets the bottom track on the same side will also be 70°. 

This is because parallel lines, when cut by a transversal, ensure that corresponding angles are equal.

Based on the location of angles on a parallel line, corresponding angles are categorized into two types. 

• Corresponding Interior Angles: These are angles on the inside of the two parallel lines where the transversal crosses them.
• Corresponding Exterior Angles: These are angles on the outside of the two parallel lines where the transversal crosses them.

Corresponding angles (whether interior or exterior) are equal in measure when the two lines are parallel. For example, if one corresponding interior angle is 70°, its matching corresponding angle (interior or exterior) will also be 70°

Corresponding Angles with Non-Parallel Lines

When a transversal intersects two non-parallel lines, corresponding angles are formed in the same matching positions relative to the transversal and the lines.  However, because the lines are not parallel, these angles are not congruent. It means their measures differ.

Example

Consider two non-parallel lines, like two roads converging toward a vanishing point, crossed by a straight path (the transversal). If the angle where the transversal meets the first road on the left side is 50°, the corresponding angle where it meets the second road in the same relative position might be, say, 45° or 55°, depending on the angle of convergence. 

Since the lines are not parallel, there’s no guarantee the angles will be equal.

Corresponding Angles Theorem

The corresponding angles theorem is also known as the Corresponding Angles Postulate. The theorem states that;

‘If a transversal cuts two parallel lines, the pair of corresponding angles formed are congruent (equal in measure).’ 

Example 

If parallel lines 𝑙 and 𝑚 are cut by transversal 𝑡, the eight angles formed include four pairs of corresponding angles. The theorem states that each pair is congruent. For instance, if one angle measures 120∘, its corresponding angle also measures 120∘

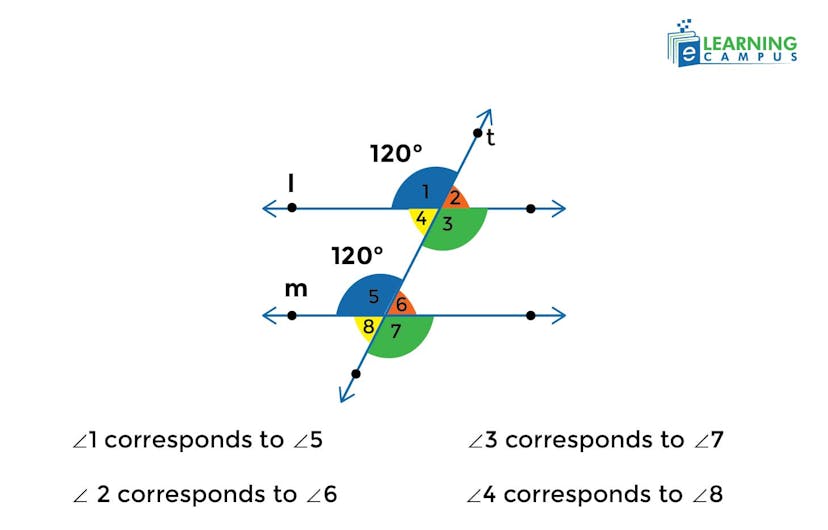
Converse of Corresponding Angles Theorem

The converse of the corresponding angles theorem is the reverse of the original Corresponding Angles Theorem or Postulate. It states that ‘if two lines are cut by a transversal and the corresponding angles formed are congruent, then the two lines are parallel.’

In simpler terms, the corresponding angles theorem and the converse theorem are differentiated as;

• Original Theorem: If lines are parallel, then corresponding angles are equal.
• Converse Theorem: If corresponding angles are equal, then the lines are parallel.

How to Find the Corresponding Angles

To find the corresponding angles, we need to identify a transversal and look for angles that are in the same relative position at each intersection. 

Steps to Find Corresponding Angles

• Identify the transversal: This is the line that intersects the other two lines. 
• Identify the intersection points: There will be two intersections where the transversal crosses the other two lines. 
• Locate angles in the same relative position: At each intersection, four angles are formed. Corresponding angles are the angles that occupy the same corner, such as both top-left, both top-right, both bottom-left, or both bottom-right at each of the two intersections. 
• Look for the 'F' shape: Imagine the lines and the transversal forming an 'F' shape. The two angles at the arms of this 'F' are corresponding angles. The 'F' can be oriented normally, upside-down, or backwards. 
• Check for congruence: If the two lines being crossed by the transversal are parallel, then the corresponding angles will have the same measure. If the lines are not parallel, the corresponding angles will not be congruent. 

We will look at some of the solved examples of corresponding angles. 

Example 1: 

The two corresponding angles measure (3x +10)° and 100°. Find the value of x.

We will use the corresponding angles theorem here. It states that two corresponding angles are equal. So, 

(3x +10)°=100°

3x=100°-10°

3x=90°

x=90°3

x=30°

Example 2

The two corresponding angles are given as 8y-16 and 6y + 4. Find the corresponding angle’s magnitude.

According to the theorem, two corresponding angles are congruent. 

8y-16= 6y + 4

8y-6y= 4+16

2y= 20

y= 202

y= 10

Corresponding Angles in Triangles

The concept of Corresponding angles is used in triangles to compare two triangles that are similar or congruent. The corresponding angles are pairs of angles that are in the same relative position in each triangle.

Two triangles are similar if their corresponding angles are equal and their corresponding sides are in proportion.

If triangle ABC is similar to triangle DEF, then:

• Angle A is equal to Angle D (∠A = ∠D)
• Angle B is equal to Angle E (∠B = ∠E)
• Angle C is equal to Angle F (∠C = ∠F)

Difference Between Vertical and Corresponding Angles

Vertical and corresponding angles are usually confused. A pair of angles cannot be both vertical and corresponding at the same time. Because by definition;

• Vertical angles are opposite angles formed by the intersection of two lines at a single vertex.
•  Corresponding angles are in the same relative position at two different intersections when a transversal line crosses two other lines. 

Sum of Corresponding Angles

In geometry, angles can be added. For example, complementary angles add up to 90∘, and supplementary angles add up to 180∘. But corresponding angles do not inherently sum to a specific value like 90° or 180°. Their sum can only be 180 if the transversal forms a right angle with the parallel lines.   

Corresponding Angles Examples in Real Life

The corresponding angles have several applications in real life. These angles are essential in fields like architecture, engineering, and construction for creating aligned structures and distributing loads evenly. 

Here are some examples of corresponding angles.

Highway Intersections

Parallel roads and side streets intersected by a crossing lane create corresponding angles.

Window Grills

The parallel bars of a window or fence cut by a diagonal bar form corresponding angles at each intersection. 

Building Designs

Architects use corresponding angles to design perfectly aligned walls, windows, and roofs.

Traffic Engineering

Traffic engineers use corresponding angles to design safe and efficient highway interchanges and traffic flow patterns.   

Conclusion 

Corresponding angles are pairs of angles in the same position at each intersection where a transversal line cuts two other lines. When the two lines are parallel, these corresponding angles are congruent (equal). We can identify corresponding angles by looking for matching positions at both intersection points.