Alternative Interior Angles
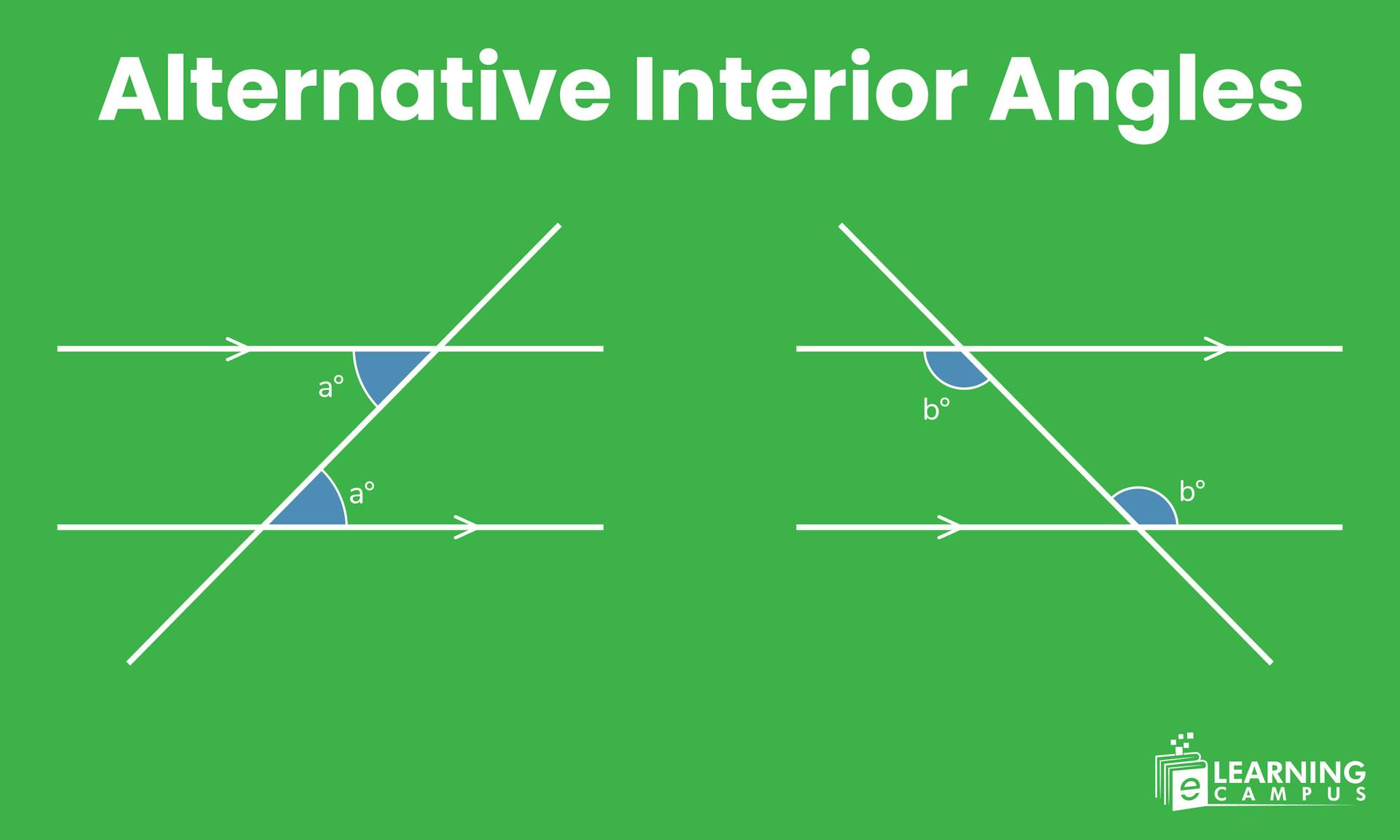
Have you ever noticed how parallel lines and a crossing line create interesting angle patterns? These patterns follow specific rules that make geometry predictable and fun. One of the most important patterns involves alternate interior angles.
Alternate interior angles are a pair of non-adjacent angles formed on the inner side of two lines (which may or may not be parallel) and on opposite sides of a third line called a transversal.
In this blog, we will break down everything you need to know about these special angles in a way that's easy to understand.
What Are Alternate Interior Angles?
Alternate interior angles are pairs of angles that form when a line crosses two parallel lines. The word "interior" means these angles are on the inside (between the two parallel lines), and "alternate" means they are on opposite sides of the crossing line.
Also, learn about complementary angles
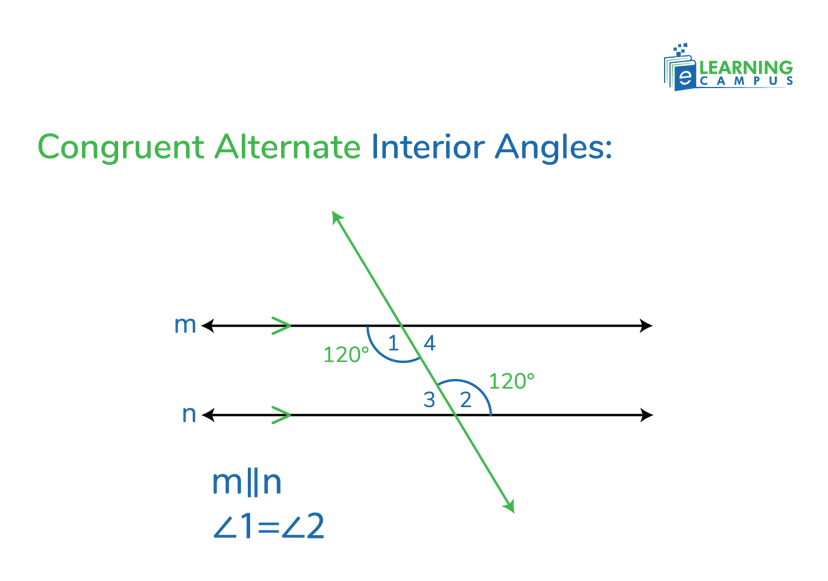
Congruent Alternate Interior Angles
Congruent alternate interior angles are formed when a transversal line intersects two parallel lines. They are always the same in the measurement.
Example
If you have parallel lines cut by a transversal, and one alternate interior angle measures 120°, the other alternate interior angle will also measure 120°.
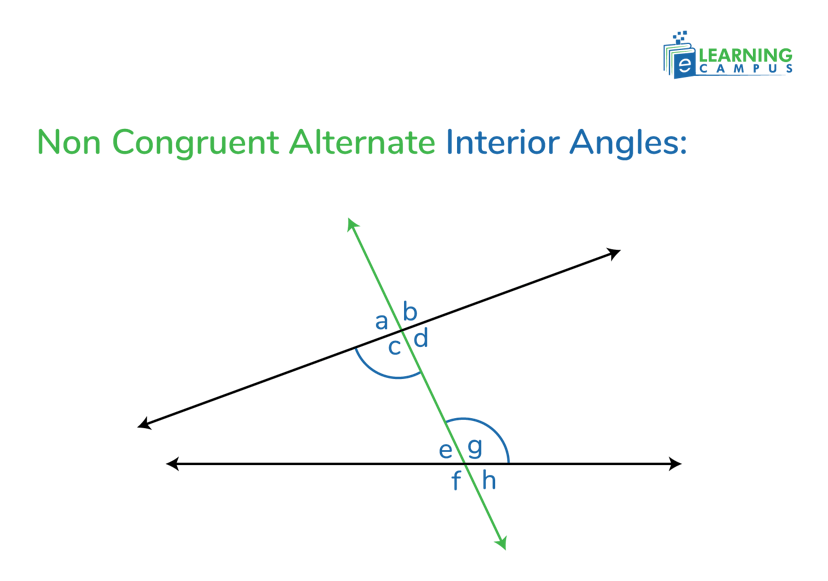
Non Congruent Alternate Interior Angles
Non-congruent alternate interior angles are the pairs of alternate interior angles that are formed when a transversal line intersects two lines that are not parallel.
Their measures are not equal. There is no relationship that can be used to determine one angle's measure from the other, as there is with parallel lines.
In the image below, angles c and g are non-congruent alternate interior angles.
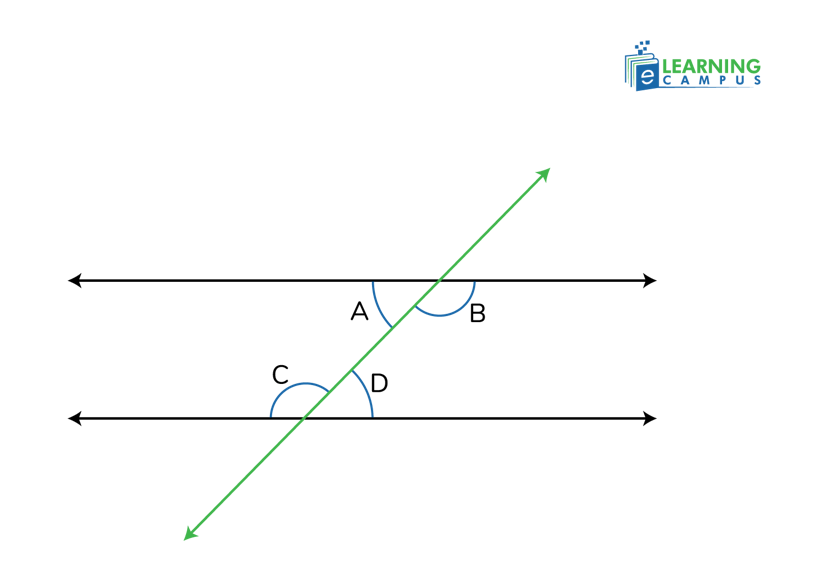
Practical Example of Alternate Interior Angles
Imagine two parallel train tracks running side by side. Now, picture a road crossing both tracks diagonally. Where the road crosses each track, angles are formed. The angles that are inside the train tracks but on opposite sides of the road are alternate interior angles.
In the image below, the angles A and D are alternate interior angles.
Definition of alternate interior angles in geometry: When a transversal (a line that crosses two other lines) intersects two parallel lines, the pairs of angles that are on opposite sides of the transversal and inside the parallel lines are called alternate interior angles.
Connect with the world-class online Math tutors.
What Do Alternate Interior Angles Look Like?
The alternate interior angles are the ones that sit on opposite sides of the transversal but stay between the two parallel lines. If you mark one angle on the left side where the transversal crosses the top line, its alternate interior angle partner would be on the right side where the transversal crosses the bottom line.
They form a "Z" pattern or a backward "Z" pattern. If we spot this Z-shape in the diagram, we have found alternate interior angles.
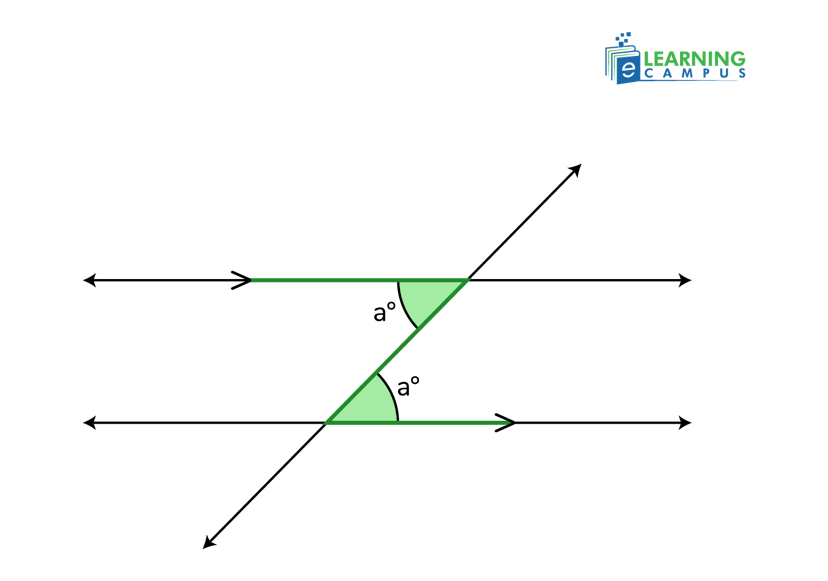
Alternate Interior Angles Theorem
The alternate interior angles theorem is a proven rule in geometry that states: ‘If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.’
This theorem works both ways:
- If we know the lines are parallel, we can conclude the alternate interior angles are equal
- If we know the alternate interior angles are equal, we can conclude the lines are parallel
This makes the theorem useful for solving problems. It can be used to find the missing angle measurements or to prove that lines are parallel.
Are Alternate Interior Angles Supplementary?
No, alternate interior angles are not supplementary. They are congruent (equal).
Supplementary angles add up to 180 degrees. That is not what happens with alternate interior angles. Instead, they have the same measurement. So if one angle is 70 degrees, the other is also 70 degrees, not 110 degrees.
- Consecutive interior angles (also called co-interior angles) are supplementary. These are different from alternate interior angles. They are on the same side of the transversal, not opposite sides.
Hire a perfect Math tutor for your kids online
Do Alternate Interior Angles Equal Each Other?
Yes, alternate interior angles are equal to each other when formed by parallel lines and a transversal. This is the key property that makes them so useful in geometry.
Whether the angles measure 30 degrees, 90 degrees, or 145 degrees, the alternate interior angles will match perfectly. This equality is what makes solving geometry problems possible.
Once you know one angle's measurement, you automatically know its alternate interior angle partner.
Are Alternate Interior Angles Congruent?
Yes, alternate interior angles are congruent when the lines are parallel. This means they have the same measure.
When a transversal crosses two parallel lines, the alternate interior angles will always be equal. This is called the Alternate Interior Angles Theorem.
For example, if one alternate interior angle measures 65 degrees, its partner angle will also measure 65 degrees.
Solving Alternate Interior Angles Problems
To solve the problems involving alternate interior angles, follow these simple steps:
- Identify the parallel lines in your diagram
- Find the transversal (the line crossing the parallel lines)
- Locate the angles between the parallel lines on opposite sides of the transversal
- Apply the theorem, which states that these angles are equal
- Set up an equation if needed and solve for the unknown
The alternate interior angles theorem only works when lines are parallel. Always check if the problem states or shows that the lines are parallel before applying the theorem.
Solved Examples of Alternate Interior Angles
Example 1: Two parallel lines are crossed by a transversal. One alternate interior angle measures 55 degrees. What does the other alternate interior angle measure?
Answer: 55 degrees (because alternate interior angles are congruent)
Example 2: In a diagram with parallel lines, you see an alternate interior angle of 120 degrees. What's its partner angle?
Answer: 120 degrees (they're equal)
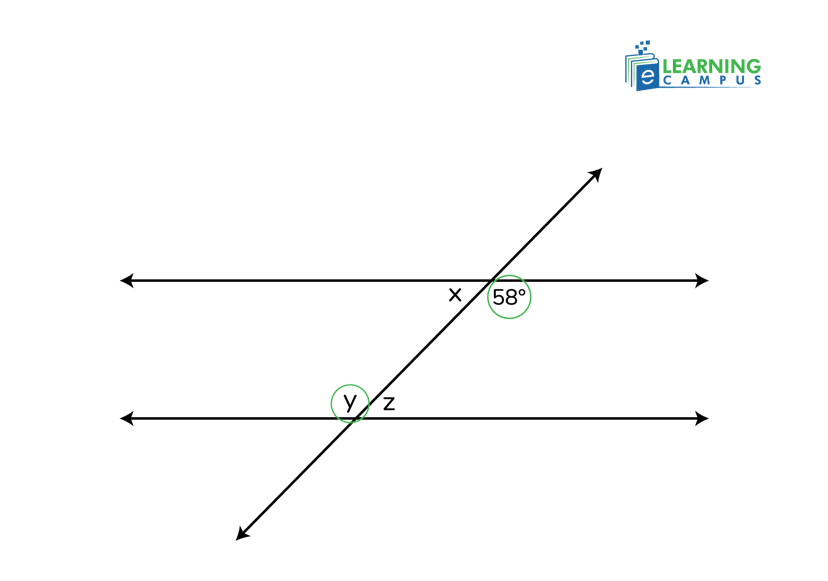
Example 3: If alternate interior angles measure (3x + 10) degrees and (2x + 30) degrees, and the lines are parallel, find x.
Since they are equal, we can write it as:
3x + 10 = 2x + 30
By combining the same terms on both sides, we get;
3x -2x=30-10
x=20
Put the value of x in both equations to find the angles.
3x + 10 = 2x + 30
3(20) + 10 = 2(20) + 30
60 + 10 = 40 + 30
70 = 70
So, the alternate interior angles are 70 degrees.
Alternate Interior Angles in Triangles
Alternate interior angles also appear when working with triangles, especially when dealing with parallel lines and triangles together.
Imagine a triangle where one side is extended to create a transversal, and there's a line parallel to the opposite side. The alternate interior angles formed can help you find missing angles in the triangle.
The concept is used as part of the proof for the Triangle Sum Theorem, which states that the interior angles of any triangle always add up to 180°.
By drawing a line parallel to one side of the triangle through the opposite vertex, you create alternate interior angles that help demonstrate this important property.
Alternate Interior Angles vs Opposite Interior Angles
The term "opposite interior angles" is another way to refer to alternate interior angles. Both terms describe the same concept, that the angles on opposite sides of the transversal that sit between the parallel lines.
Some textbooks use "alternate," others use "opposite," but they mean the same thing.
Common Mistakes to Avoid in Alt Interior Angles
Many students confuse alternate interior angles with other angle types. Here are the key differences:
- Alternate exterior angles: These are outside the parallel lines, not inside
- Corresponding angles: These are on the same side of the transversal and in matching positions
- Consecutive interior angles: These are on the same side of the transversal, and they are supplementary, not congruent.
The word "alternate" means opposite sides. The word "interior" means between the lines.
Why Are Alternate Interior Angles Important?
The alt interior angles have several implications in daily life. Understanding them helps you:
- Solve for unknown angles quickly
- Prove lines are parallel
- Work with more complex geometric shapes
- Understand real-world applications like architecture and engineering
They appear in bridges, buildings, road intersections, and anywhere parallel lines exist in the real world. Architects and engineers use these principles when designing structures to ensure everything aligns correctly.
Conclusion
Alternate interior angles are formed when a transversal line crosses two other lines. They are congruent (equal in measure) only if the two lines being intersected are parallel. If the lines are not parallel, the alternate interior angles are not congruent and have no special relationship to each other.
