What Does Delta Mean in Math

Have you ever encountered a small triangular symbol while solving a calculus or algebraic problem? Or maybe you are reading about scientific experiments and keep seeing this symbol appear in equations about change and difference. This triangular symbol is a delta. 

Delta represents change. It is one of the most important symbols in all of mathematics. From ancient Greece to modern engineering, it has been used as a language for expressing change, difference, and variation. 

In this blog, we will shed light on what delta means in Math and how it is used in different contexts. 

What is the Delta in Math

Delta is one of the fundamental concepts in Mathematics. It is the fourth letter of the Greek alphabet and represented as Δ for upper case and δ for lower case. The Delta meaning in Math depends on the context it is used. The upper case delta represents a different identity than that of the lower case. 

For example, Δx represents a finite change in the variable x, while δ in calculus shows a very small change. 

You can also learn to convert an improper fraction to a mixed number

What is the Delta Symbol in Math

Delta is a mathematical symbol for change. It is represented by two symbols, i.e, upper case delta and lower case delta. 

• The symbol for upper case delta is Δ. It represents a finite or measurable change in a value
• The symbol for lower-case delta is δ. It represents an infinitesimal or very small, unmeasurable change

How do We Use Delta in Mathematics

Both upper-case and lower-case delta have practical applications in mathematics. They represent change or difference. From Algebra to calculus, Mathematicians use it for variations in quantities, functions, and geometric properties.

Use of Delta in Algebra

In algebra, delta (Δ) is used primarily for the following purposes

• Discriminant of a quadratic equation (uppercase Δ): This is one of the most common applications of delta in algebra.
• Representation of change (uppercase Δ): This is often used in coordinate geometry to express the change in a variable.
• Symmetric difference in set theory (uppercase Δ): it represents the elements that are in one of two sets but not both.
• The Kronecker delta (lowercase δ): it shows of function of two variables that is 1 if they are equal and 0 if they are not.

Discriminant of a Quadratic Equation

Delta is used to represent the discriminant of a quadratic equation. Its value tells the nature of the equation's solutions. For a quadratic equation in the standard form

the discriminant Δ will be calculated as:

The value of the discriminant in this case is the nature of the equation's roots. 

If, 

Δ>0: There are two distinct real roots.

Δ=0: There is exactly one real root (a repeated or double root).

Δ<0: There are no real roots. The solutions are a pair of complex conjugates.

Example 

Consider that we have the quadratic equation

We can easily separate the coefficients and the constant.  

Now, we can easily find the discriminant of the equation. 

So, the discriminant of the equation is greater than zero (Δ > 0). It means the equation has two real roots.

Representation of Change

Delta symbols in math always represent change. In coordinate geometry, the uppercase delta symbol (Δ ) is used to represent a change in a variable. This is used in the formula for the slope of a line. Such as;

Where,

Δy represents the change in the y-values.

Δx represents the change in the x-values

Symmetric Difference of Sets

The delta symbol in math is also used to represent the symmetric difference of two sets. The symmetric difference of two sets A and B is the set of elements that are in either A or B, but not in their intersection. It is represented as AΔB. 

The symmetric difference can be represented using other set operations. 

Example 

Find the symmetric difference for these sets.

Find A - B: The elements present in A but not in B are {1, 2, 3}

Find B - A: The elements that are in B but not in A are {6, 7}

Take the union of the sets: The symmetric difference is the union of these results. 

The Kronecker delta

In more advanced algebra, the lowercase delta (δ) is used to define the Kronecker delta δij. It is a function of two variables, i and j, that are typically non-negative integers. It is represented as; 

This is used in linear algebra to represent the entries of the identity matrix. 

The concept of Delta is mostly asked in admission tests such as the SAT. You can prepare for SAT online with expert SAT tutors. 

Use of Delta in Calculus 

In calculus, Delta represents a change or a difference in a quantity. The uppercase Delta (Δ) shows a finite, measurable change in a quantity, such as in the slope formula (Δy/Δx). The lowercase delta (δ) shows a small or near-zero change. 

Uppercase Delta (Δ)

The upper-case delta is used to represent the concepts that form the foundational ideas of calculus. It shows a finite and measurable change between two values. It is used in;

Definition of the Derivative

The derivative is fundamentally the limit of the average rate of change. Delta (Δ) is used to express the average rate of change before taking the limit to find the instantaneous rate of change. 

The average rate of change of a function fx over an interval is the change in y divided by the change in x and represented as;

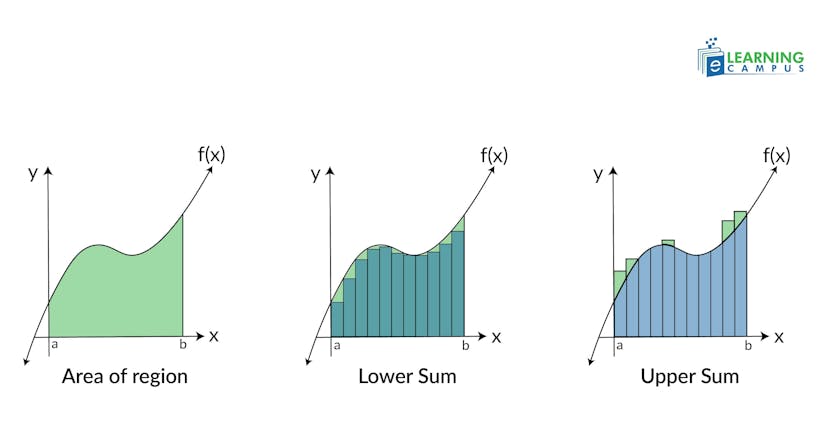
Riemann sums

Delta plays a crucial role in Riemann Sums. It represents the width of the rectangles that are used to find the approximate value of the area under a curve. As the number of rectangles increases, x decreases, which is part of the process of taking an integral. 

Lowercase Delta (δ)

The lowercase delta (δ) is commonly used in calculus proofs. It is used for the epsilon-delta definition of limits and to represent partial derivatives in multivariable functions.

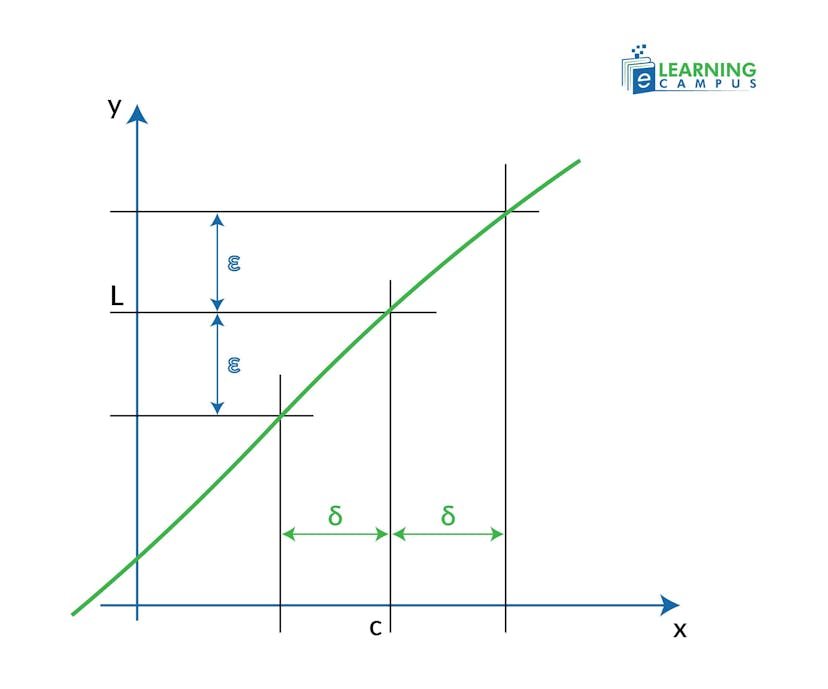
Epsilon-delta Definition of a Limit

The formal definition of a limit, known as the "epsilon-delta proof," uses (δ) to define the input tolerance. The definition states that;

The limit of f(x) as x approaches c is L if for any positive number ε, there exists a positive number δ such that if the distance between x and c is less than δ, then the distance between f(x) and L is less than ε.

In this context, the lower-case delta (δ) represents a small distance from c on the x-axis, corresponding to a small distance ε from L on the y-axis. 

Partial Derivatives

The delta sign in mathematics is used in multivariable calculus. The partial derivative operator ∂, an alternative form of the lowercase delta, represents the rate of change of a multivariable function with respect to just one variable. While holding all other variables constant. 

For a function, f(x,y)  the partial derivative with respect to x is denoted as

What are the Math Symbols Similar to Delta

There are many symbols in mathematics and other disciplines that resemble the uppercase Delta or lowercase delta. But they represent different concepts. 

• The Nabla symbol (∇): This symbol is commonly confused with the uppercase delta. It resembles an upside-down delta that represents the "del" operator. It is mostly used in vector calculus to find gradients, curls, and divergences.
•  Triangle symbols △: This symbol is used in geometry to show the area of a triangle, such as △ABC. 
• Partial derivative symbol ∂: This curved symbol resembles lower-case delta in math. It is used in multivariable calculus to represent a partial derivative. It measures how a function changes with respect to one variable while others are held constant.
• Latin letter "d" (𝑑): the letter 𝑑 represents an infinitesimal change, or differential in single-variable calculus. It is represented as

Conclusion 

The symbol delta (Δ or δ) represents a change or difference between two values or quantities. Uppercase delta (Δ) shows a larger, finite change, while lowercase delta (δ) represents a very small, infinitesimal, or "approaching zero" change. It is widely used in math, including geometry and calculus. It helps to calculate the slope of a line (Δy/Δx) and find the discriminant of a quadratic equation (Δ = b² - 4ac).