elearning BlogVertex Formula for Parabolas

Vertex Formula for Parabolas

 Vertex Formula for Parabolas

When working with quadratic equations and parabolas, one of the most important points you will need to identify is the vertex. The vertex represents either the highest or lowest point on a parabola, and understanding how to find it is essential for graphing and analyzing quadratic functions.

What is the Vertex Formula?

The vertex formula is a mathematical equation that helps find the coordinates of a parabola's vertex directly from a quadratic equation. For a quadratic equation written in standard form as y = ax² + bx + c, the vertex formula gives you the x-coordinate of the vertex:

x = -b/(2a)

Once you have this x-coordinate, you can substitute it back into the original equation to find the corresponding y-coordinate, giving you the complete vertex point (h, k).

Understanding Vertex Form

Before diving deeper into the vertex formula, it's helpful to understand vertex form itself. A quadratic equation in vertex form looks like this:

y = a(x - h)² + k

In this format, the vertex of the parabola is simply (h, k). This makes vertex form incredibly useful when you need to quickly identify the vertex or graph a parabola. The value of 'a' still determines whether the parabola opens upward (a > 0) or downward (a < 0), as well as how wide or narrow the parabola appears.

How to Find the Vertex of a Quadratic Formula

Let's walk through the process of finding the vertex using the vertex formula for a parabola.

Step 1: Identify a, b, and c

Starting with your quadratic equation in standard form (y = ax² + bx + c), identify the coefficients. For example, in the equation y = 2x² - 8x + 5:

  • a = 2
  • b = -8
  • c = 5

Step 2: Apply the vertex formula

Use the formula to find the x-coordinate of the vertex

x=−b2ax = -\frac{b}{2a}
x=−−82(2)x = -\frac{-8}{2(2)}
x=84x = \frac{8}{4}
x=2x = 2

Step 3: Find the y-coordinate

Substitute x = 2 back into the original equation:

y = 2(2)² - 8(2) + 5

y = 8 - 16 + 5

y =  -3

Step 4: Write the vertex

The vertex is (2, -3).

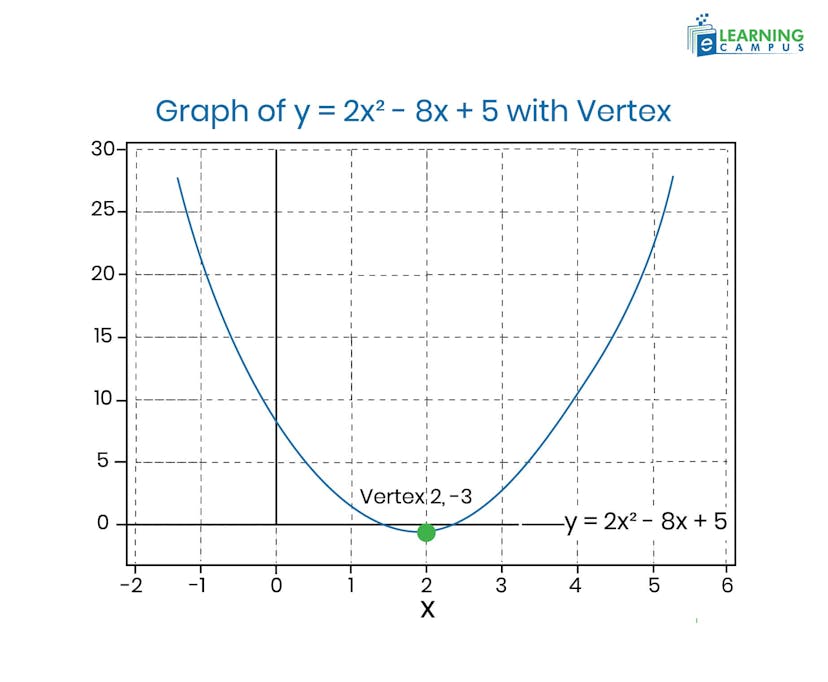
How to Find the Vertex of a Quadratic Formula

The graph shows the parabola y = 2x2 - 8x + 5 with the vertex clearly marked at (2, -3). Since the coefficient a = 2 is positive, the parabola opens upwards.

Converting Standard to Vertex Formula

Many students wonder how to write a quadratic formula in vertex form when it's given in standard form. This process is called completing the square, and it's an algebraic method that transforms the equation's structure.

For the equation y = ax² + bx + c, here's the general approach:

  1. Factor out 'a' from the first two terms if a ≠ 1
  2. Complete the square inside the parentheses
  3. Simplify to get the form y = a(x - h)² + k

Alternatively, you can use the vertex formula to find (h, k) and then write the equation directly in vertex form.

Vertex Formula Calculator Approach

While you can certainly use a vertex formula calculator to check your work, understanding the manual process helps build mathematical intuition. The formula for finding the vertex is straightforward enough that with practice, you'll be able to calculate it quickly without technological assistance.

Why the Vertex Formula Matters

The formula for the vertex of a parabola is more than just an academic exercise. It has practical applications in physics, engineering, and economics. For instance:

  • Projectile motion: The vertex represents the maximum height of a thrown object
  • Business optimization: Finding maximum profit or minimum cost in quadratic models
  • Architecture: Designing parabolic arches and structures

The Vertex Formula of a Quadratic Function

It's worth noting that the vertex formula for a quadratic equation works for any parabola represented by a quadratic function. Whether you're working with a simple equation like y = x² or a more complex one like y = -3x² + 12x - 7, the same formula applies.

The formula of the vertex of a parabola (x = -b/(2a)) is derived from calculus, where it represents the point where the derivative of the quadratic function equals zero, the point of zero slope where the parabola changes direction.

How do you find the vertex of a quadratic formula quickly?

The fastest method is to use x = -b/(2a), then substitute to find y. This is much quicker than completing the square for most problems.

How to find 'a' in vertex form?

If you're given a vertex and another point on the parabola, you can substitute these values into y = a(x - h)² + k and solve for a.

What is the formula for vertex?

The primary formula is x = -b/(2a) for the x-coordinate, combined with substitution to find y. Alternatively, when in vertex form, the vertex is simply (h, k).

Practical Example

Let's work through a complete problem. Find the vertex of the parabola y = -x² + 6x - 5.

Using the vertex formula:

  • a = -1, b = 6, c = -5
  • x = -6/(2 × -1) = -6/(-2) = 3
  • y = -(3)² + 6(3) - 5 = -9 + 18 - 5 = 4

The vertex is (3, 4), which is a maximum point since a < 0.

Derivation of Vertex Formula

We know that the standard form of a parabola is,

y=ax2+bx+cy = ax^2 + bx + c

We can convert it into the vertex form;

y=a(x−h)2+ky = a(x - h)^2 + k

through completing the squares.

Subtracting c from both sides:

y−c=ax2+bxy - c = ax^2 + bx

Take a as the common factor, then

y−c=a(x2+bax)y - c = a(x^2 + \frac{b}{a}x)

Half of the coefficient of x is:

b2a\frac{b}{2a}

and square is:

b24a2\frac{b^2}{4a^2}

Add and subtract this on the right side.

y−c=a(x2+bax+b24a2−b24a2)y - c = a(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} - \frac{b^2}{4a^2})

We can write:

x2+bax+b24a2=(x+b2a)2x^2 + \frac{b}{a}x + \frac{b^2}{4a^2} = (x + \frac{b}{2a})^2

So, the above equation will become:

y−c=a((x+b2a)2−b24a2)y - c = a\left((x + \frac{b}{2a})^2 - \frac{b^2}{4a^2}\right)

Distribute a on the right side and add c on both sides:

y=a(x+b2a)2−b24a+cy = a(x + \frac{b}{2a})^2 - \frac{b^2}{4a} + c
y=a(x+b2a)2−b2−4ac4ay = a(x + \frac{b}{2a})^2 - \frac{b^2 - 4ac}{4a}

Comparing this with:

y=a(x−h)2+ky = a(x - h)^2 + k

we get:

h=−b2ah = -\frac{b}{2a}
k=−b2−4ac4ak = -\frac{b^2 - 4ac}{4a}

We know that:

b2−4acb^2 - 4ac

is the discriminant (D).

Thus, the vertex formula is:

(h,k)=(−b2a,−D4a)(h, k) = \left(-\frac{b}{2a}, -\frac{D}{4a}\right)

where:

D=b2−4acD = b^2 - 4ac

Conclusion

The vertex formula is an essential tool for anyone working with quadratic equations and parabolas. It helps convert from standard to vertex formulae or to find the vertex of a parabola. With practice using the formula for finding the vertex, you will develop the confidence to tackle more complex problems involving quadratic functions.

FAQs