Trigonometric Ratios

The trigonometric ratios are ratios of the lengths of two sides of a right triangle. There are 6 trigonometric ratios. The most common are sine, cosine, and tangent, and the other 3 ratios are cosec, sec, and cot. In trigonometry, these ratios represent the relationship between the lengths of the sides of the triangle and the measure of its acute angles.

What are Trigonometric Ratios 

The six ratios, namely sin, tan, cos, cot, csc, sec, are known as the trigonometry ratios. In short, the values of all trigonometric functions derived from the ratio of a right-angled triangle's sides are termed the trigonometric ratios. 

How to Find Trig Ratios

Each trigonometric ratio has a value. These values can be calculated using the measure of an acute angle (θ) of the given right triangle.  Let’s learn how to find trig ratios.

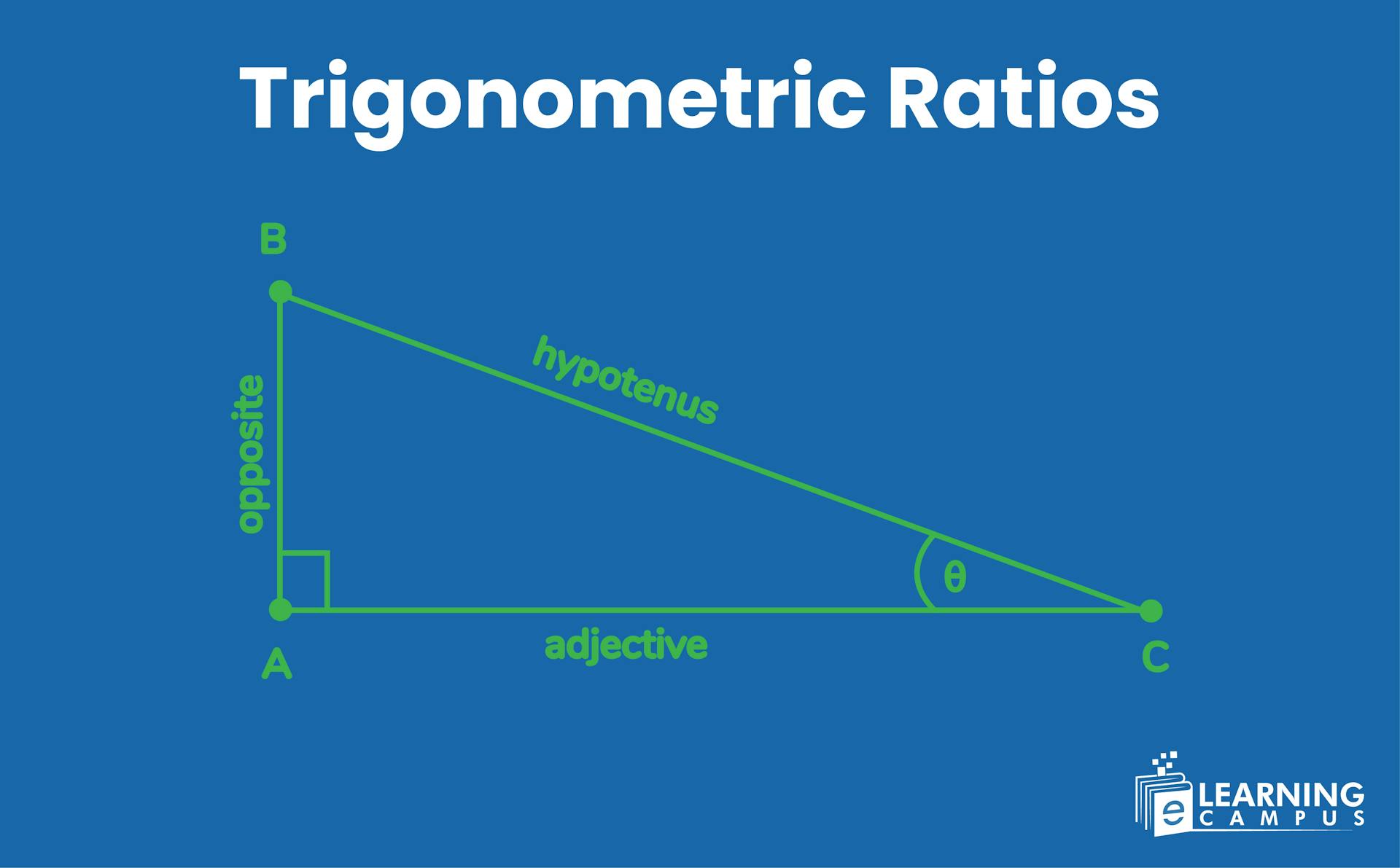
Let us consider a right triangle ABC, with an angle θ (theta). 

In the right triangle below, we will term the three sides opposite, adjacent, hypotenuse in relation to the angle or theta (θ).

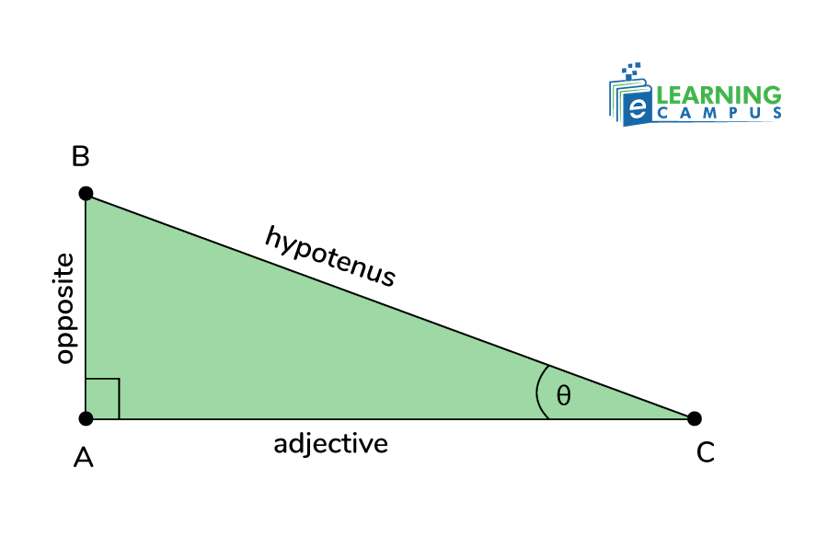
• Hypotenuse: The side that appears opposite to a right angle is the hypotenuse. 
• Opposite: the side that lies opposite to an angle (θ) is the opposite of perpendicular.
• Adjacent: the side next to angle (θ) is termed as adjacent. 

With respect to (θ), the trigonometry ratios are given as:

• Sin: the Sine of an angle is the ratio of the opposite side to the hypotenuse.

• Cosine: The Cosine is the ratio of the adjacent side to that angle to the hypotenuse.

• Tangent: The tangent is the ratio of the opposite side to the side adjacent to an angle.

These ratios are the foundation of trigonometry. They can be remembered with the help of a mnemonic, SOH CAH TOH. SOH is used to remember Sin ratio. In which ‘S’ represents sin, ‘O’ shows opposite, and ‘H’ represents hypotenuse. 

CAH is used to remember the cosine ratio. In which ‘C’ is used for cosine, ‘A’ represents adjacent, and ‘H’ shows hypotenuse.

TOH is for tan ratio. In which ‘T’ stands for tangent, ‘O’ shows opposite, and ‘H’ stands for hypotenuse. 

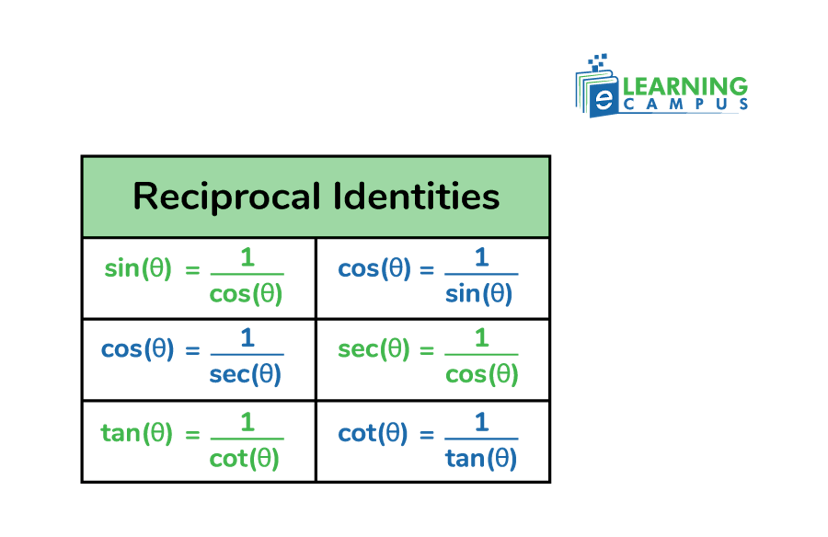
Reciprocal Identities in Trigonometry

The reciprocal identities in trigonometry relate the primary trigonometric functions (sine, cosine, tangent) with their reciprocal functions (cosecant, secant, cotangent).

Along with the above basic ratio of trigonometry, we can also find the value of csc, sec, cot. These ratios are the trigonometric reciprocals. 

• Cosecant: The cosecant is the reciprocal of sine. 

• Secant: Secant is the reciprocal of cosine. 

• Cotangent: cotangent is the reciprocal of tangent.

Trigonometric Ratios Of Angles 

We can find the trigonometric ratios for different angles such as 0°, 30°, 45°, 60°, and 90°. The value of the ratio of these angles can be used to find the value of other angles. 

The trigonometric ratios of  30° and 60° can be found with the help of an equilateral triangle of side 2 cm. 

Let us consider an equilateral triangle, whose sides are of length 2 cm. 

If we split the triangle into two equal parts, two right angles will be formed. 

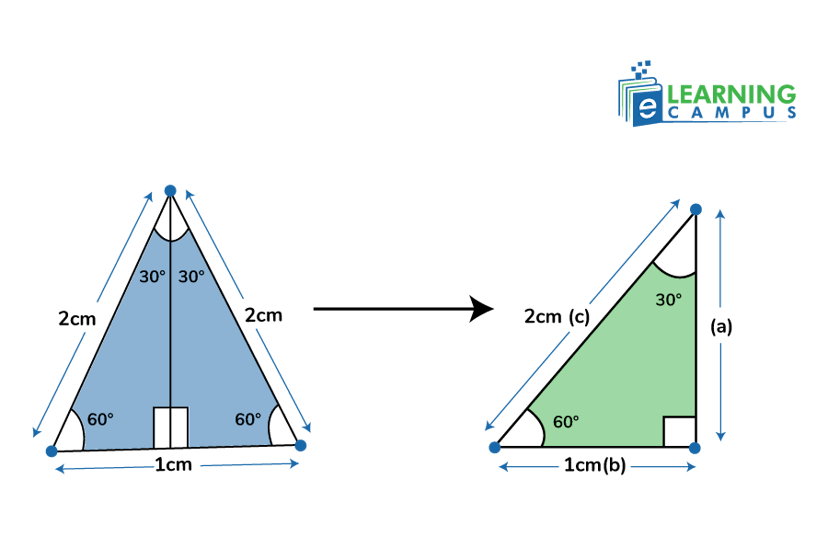
The hypotenuse (c) of the triangle is 2 cm, the base (b) is a length of 1 cm, and the hypotenuse (a) can be found using the Pythagorean theorem.

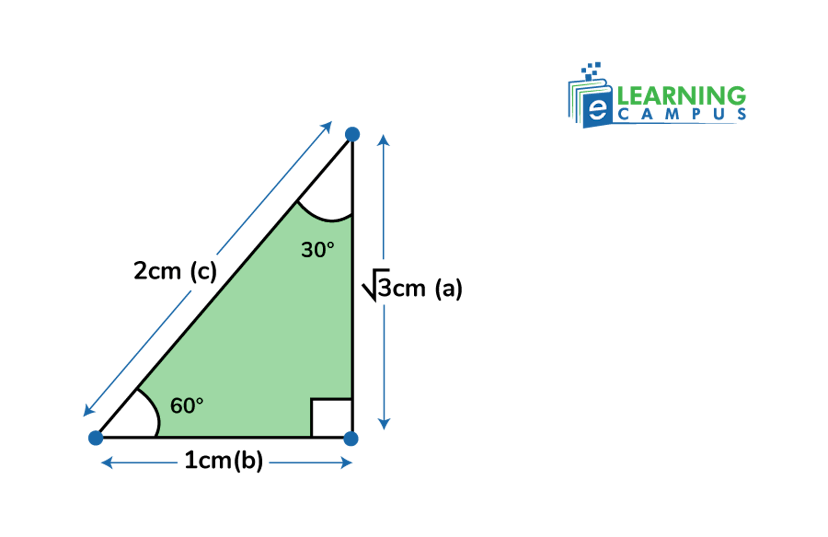
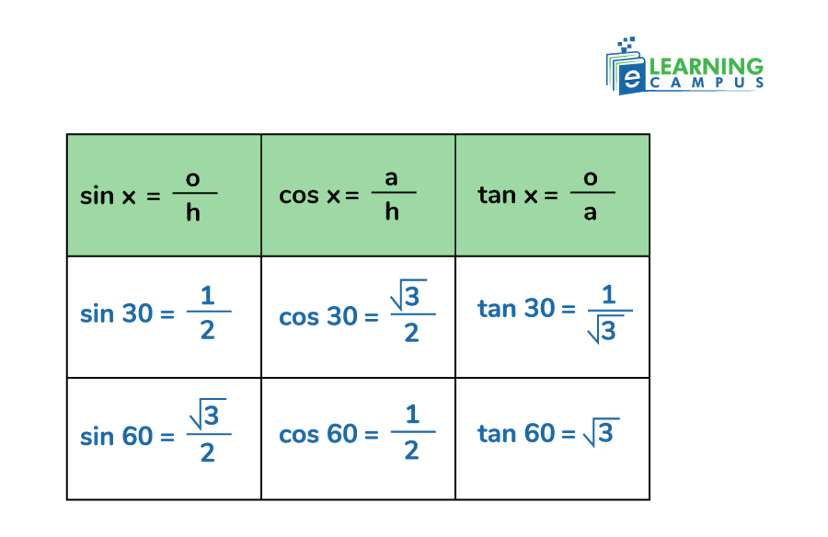
So, putting the value of the sides of a right angle, we can find the values of 30° and 60°, which are shown in the table below. 

In the same way, the trigonometry ratio of  45° can be found with the help of a square with sides 1 cm. 

Let us consider a square with sides 1 cm each. We can split the square into two halves. It will give 45°on two edges. As shown below. 

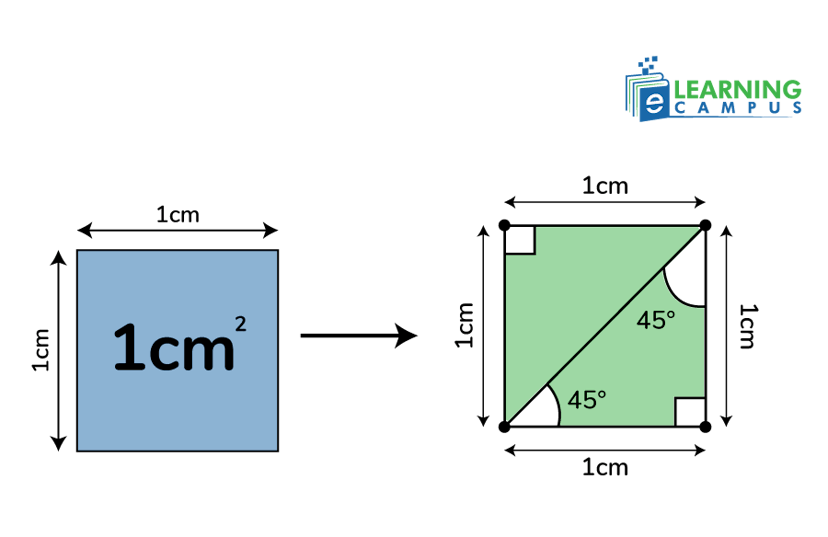
The ‘adjacent’ and ‘opposite’ of a triangle are 1 cm each. The hypotenuse can be found by using the Pythagorean theorem.

So, the hypotenuse is

Based on the above calculation, the values for the angle 45° are given below.

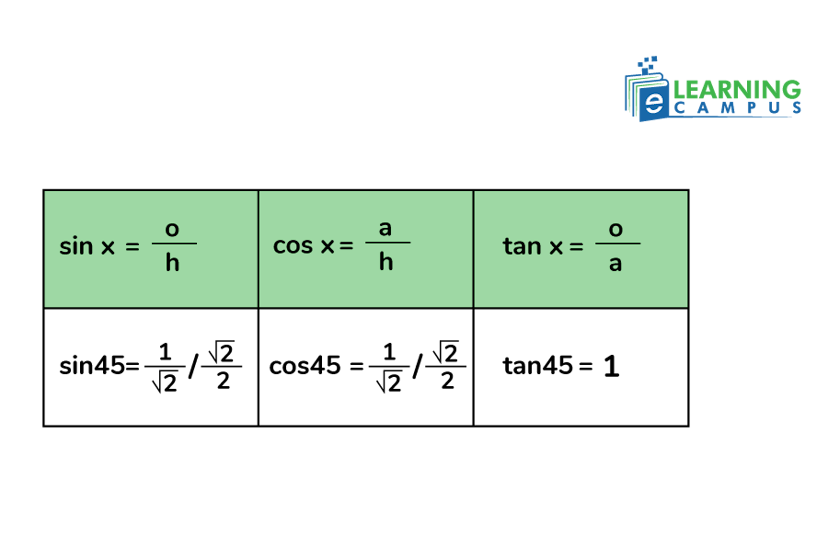
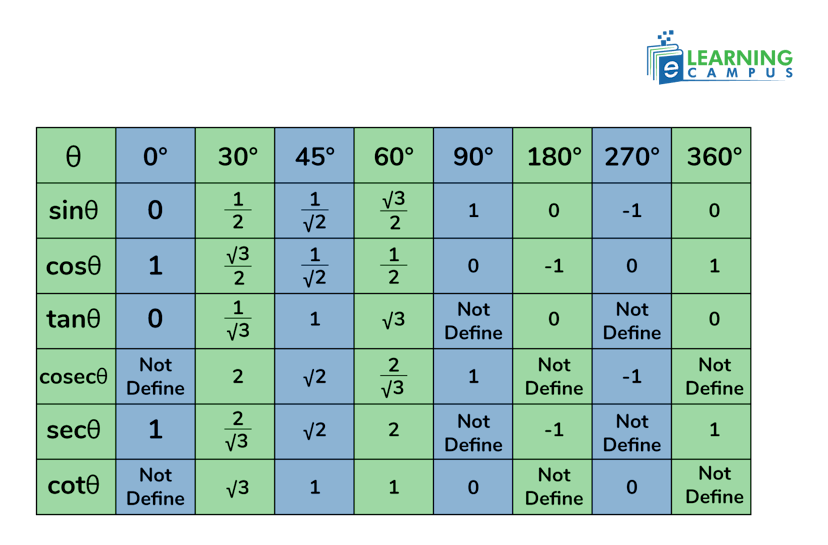
Trig Function Table

We calculated the values for different angles with the help of a triangle and a square. The values of the right angle triangle ratios for specific angles such as 0°, 30°, 45°, 60°, and 90° vary depending on the value of the sides of the triangle. The trig function table is shown below.

Trigonometric Ratios on a Unit Circle 

A unit circle is a circle that has a radius of 1 cm. The trigonometric functions of sine, cosine, and tangent can be calculated by using a unit circle. 

Sin and Cos on Unit Circle

The values of sin and cos on unit circle can be calculated by drawing a right triangle inside a unit circle.

Let us suppose a right angle is placed inside a unit circle in a coordinate system, as shown below. 

• The radius of the circle shows the hypotenuse of the right-angle triangle.
• The radius makes an angle θ with the x-axis.  
• The x-coordinate represents cos θ, while the y-coordinate represents sin theta, sin θ. 
• Vectors x and y represent the base and the altitude of the right-angled triangle. 

Now, we have a hypotenuse of 1 cm, base x, and perpendicular y. By applying these values in trigonometry, the value of ratios will become ;

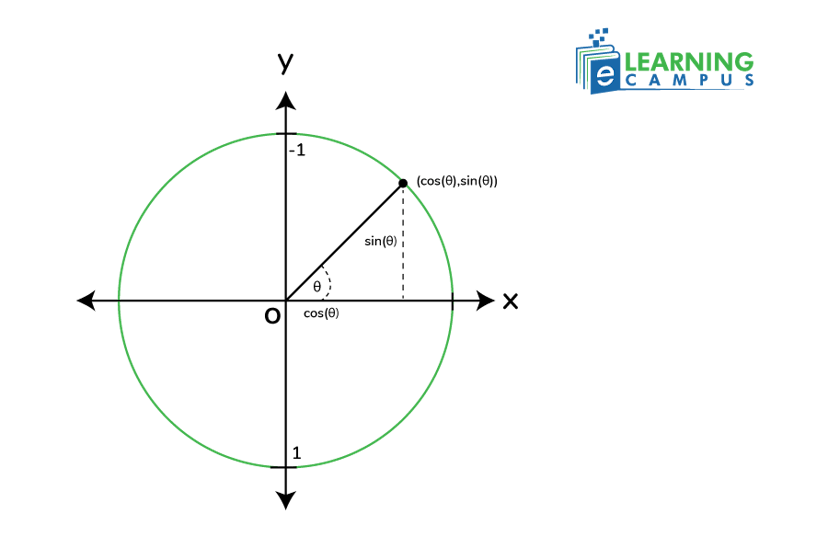
So, we found the values of cos sin on unit circle. 

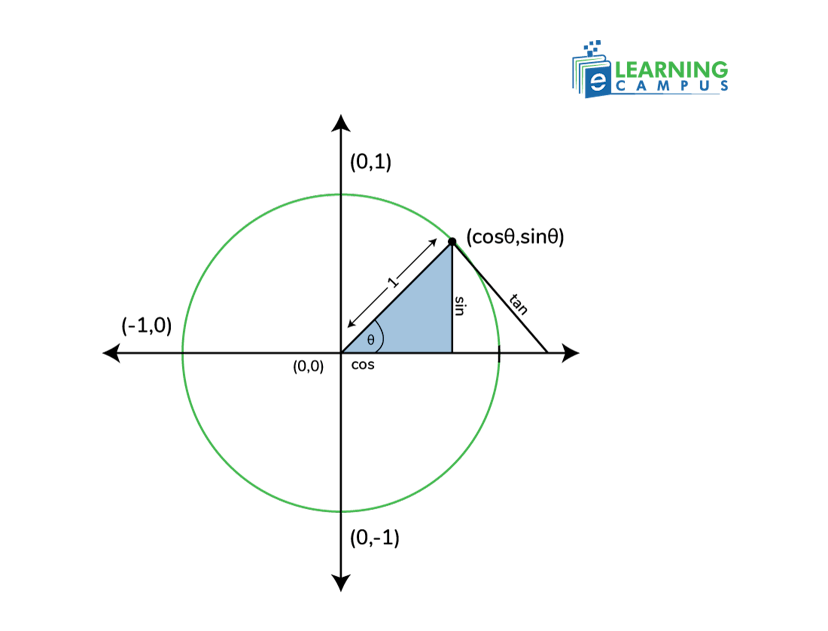
Unit Circle With Tangent

The trigonometric identities of (cosθ, sinθ) are identical to the coordinates (x, y) of any point on the unit circle. Unit circle with tangent can be calculated with the help of the values of sin theta and cos theta. 

The values of cosθ = x and sinθ = y can be further applied to get tanθ.

tan=yx

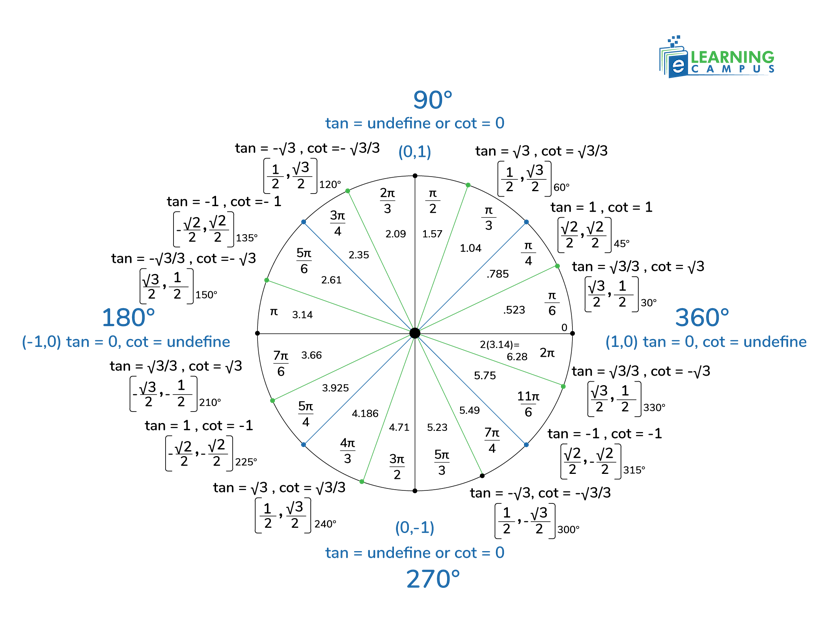
Unit Circle Chart With Sin Cos Tan

We found the trigonometric values of sin, cos, and tan. The unit circle chart with sin cos tan will help you understand the values of angles at different positions within a unit circle. 

Trigonometric Ratios Worksheet

The trigonometric ratios worksheets contain trigonometry practice problems, helping you build a strong understanding of the concepts. You can download the printable PDF on trigonometry ratios below.