Subset in Maths

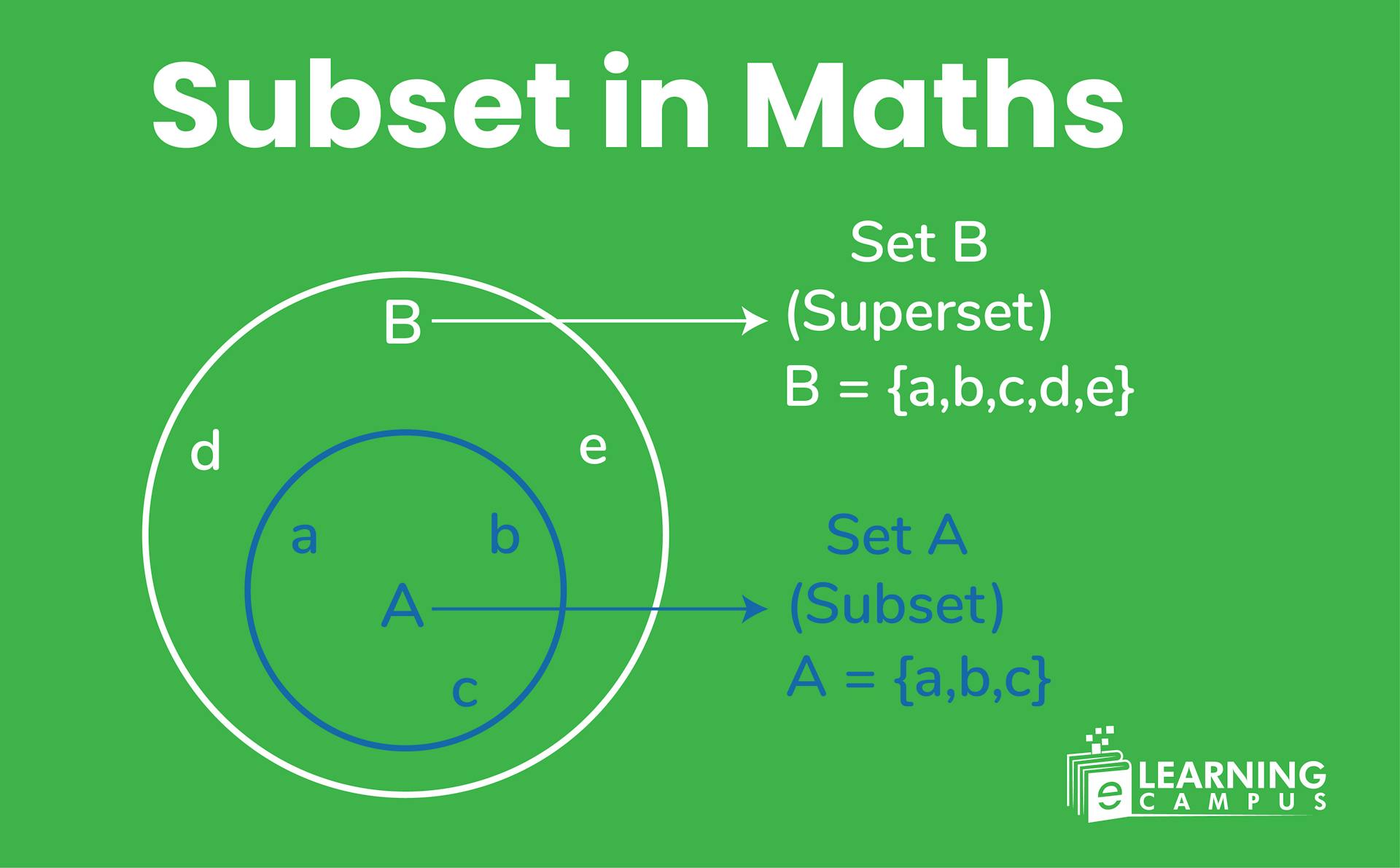
A Set and a subset in Maths are interlinked concepts. A set is a collection of anything, such as numbers, objects, or things, that are grouped in one bracket. A subset can be defined as the set that contains all elements or some of the elements of another set, known as a superset. Every set is a subset of itself. 

In this blog, you will learn about the subset, its types, symbols, and examples. 

What is a Subset in Math    

We are well aware of the concept of sets in Math. It is the collection of anything that is represented by brackets. Let’s know what is a subset in math. 

In mathematics, the subset meaning can be understood as a set where all of its elements are also members of another larger set known as the superset. 

A subset definition states that ‘if set A contains all the elements of set B, then B is considered a subset of A.’

We will understand it with the help of subset examples. 

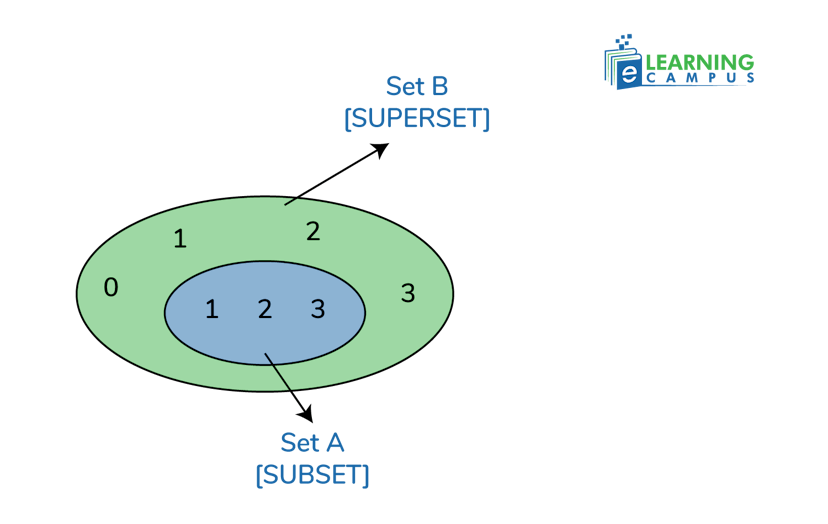
Consider two sets A and B. 

• A is the set of the natural numbers. 

• B is the set of all the whole numbers.

Then, according to the given conditions, A is the subset of B, as all natural numbers are in the set of the whole numbers. 

So, A is a subset of B. It is represented as;

Subset Formula

The subset formula tells us about the number of subsets of a set with n elements. The formula to find the number of subsets with ‘n’ elements is given as

For example, if set A has 4 elements, then the possible numbers of subsets will be,

It means a set with 4 elements can have 16 subsets. 

Types of Subsets 

There are two main types of subsets in Math, named a proper subset and an improper subset. We will understand these types in detail.   

Proper Subset

A proper subset is a subset that does not contain all the elements of another set or is not equal to the original set. It means that this subset contains fewer elements. For example, if there are two sets A and B. 

A is a subset of B because A does not contain all elements of B, 8 is missing in A. 

Proper Subset Symbol

Sets are represented by different symbols in Math. The proper subset symbol is ‘⊂’. For example, if B is a proper subset of A, then it is written as;

Proper subset formula

A Proper subset formula of a set with ‘n’ elements is given as;

If set A has 3 elements, then the proper subset of A will be calculated as;

Improper Subset 

The improper subset is either equal to the original set or the empty set. Set A is an improper subset of B if A contains all the elements of B. Every set has one improper subset that is the set itself. 

Let’s look at the improper subset examples. 

If

and B is the improper subset of A,

Then

Improper subset symbol

An improper subset is represented with the symbol ⊆.  If X is an improper subset of Y, then X ⊆ Y. The symbol  "⊆" also shows that  X is a subset of or equal to Y. The improper subset symbol can be used for a proper subset, but the proper subset symbol can’t be used for an improper subset. 

Difference Between Subset and ‘Belongs to’

Two terms, ‘subset’ and ‘belongs to’, are commonly used while dealing with subsets in Maths. Students usually find it difficult to differentiate these terms. The difference between ‘subset’ and ‘belongs to’ is that "belongs to" describes the relationship between an element and a set, while "subset" describes the relationship between two sets.

For example, set B is a subset of A if every element of B is also an element of A. It is denoted by B ⊆ A. 

The phrase ‘belongs to’ shows the relationship of an element and a set. If ‘y’ is an element of set B, then we can say that y belongs to B. It is denoted by ‘y ∈ B’.  

Conclusion  

A subset in Maths is a set whose elements are also members of another set. In simple terms, a subset is a smaller collection of elements taken from another set. There are two basic types of subsets, proper subsets and improper subsets.