Square Root of -4

Have you ever wondered what happens when we try to take the square root of negative numbers, such as √-4. The square root of negative numbers is not possible. To solve this type of problem, we need a special number called i the imaginary unit.
In this blog, we will explore how to handle square roots of negative numbers, fractions, or decimals step by step in detail.

Square Root of -4

To find the square root of -4, which is negative, we need an imaginary number. Let’s solve the square root of -4 with proper steps.

Step 01:
In real numbers, a square root of a negative number does not exist. So no real number squared gives −4. The square root of −4 is ±2i, where i represents the imaginary unit.

Step 02:
In complex numbers, we use;
i = √−1
Rewrite −4 as:
−4 = 4(−1)

Step 03:
Apply square root rules and simplify.

√−4 = √(4(−1))

Step 04:
Find the square root of 4 and put the value of i = √−1

√−4 = √4 × √(−1) = 2i = ±2i

So, −4 = ±2i

Square Root of 1/4

The square root of -4 does not exist in the real number system because no real number multiplied by itself gives a negative result.

However, in complex numbers, the square root of -4 step by step:

Step 01: Write the Expression

√(1/4)

Step 02: Apply the Square root to the Numerator and Denominator

√(1/4) = √1 / √4 (splitting the fraction)

Step 03: Find the square root and simplify it

√1 / √4 = 1 / 2

So the square root of 1/4 = 1/2

Square Root of 4/3

To find the square root of 4/3, first, apply the square root to the denominator and numerator, rationalize it, and simplify the values. Here are the steps:

Step 01: Write the Expression

√(4/3)

Step 02: Apply the square root to the numerator and denominator

√(4/3) = √4 / √3

Step 03: Find the square root and simplify it

√4 / √3 = 2 / √3

Step 04: Rationalize the denominator

To remove the square root from the denominator, multiply the numerator and denominator by √3:

(2 / √3) × (√3 / √3) = 2√3 / 3

Step 05: Multiply the values and simplify them

2√3 / 3

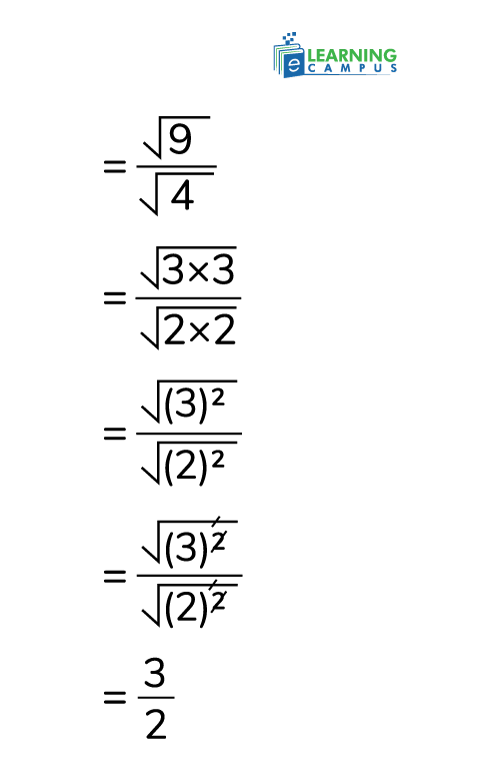
So, the square root of 9/4 = 3/2, also a rational number.

What is the Square Root of 2/4

If you want to find the square root of 2/4, then you need to write it as an expression. Apply the square root to the numerator and denominator, and simplify the values.

Step 01: Write the Expression

√(2/4)

Step 02: Apply the square root to the numerator and denominator

√(2/4) = √2 / √4

So, the square root of 2/4 is √2 / 2

What is the Square Root of 4

The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 4 is 2, which is a rational number because it can be written as a fraction.

Step-by-step calculations:

√4

Step 01: Find the factors of 4

2 × 2 = 4

Step 02: Cut the square root of 2

(√2)² = 2

So, the square root of 4 is 2.

Square Root of 4.5

If you want to find the square root of 4.5, then you need to write it as a fraction. Apply the square root to the numerator and denominator, rationalize it, and simplify the values.

Step 01: First, write 4.5 as a fraction

4.5 = 9/2

Step 02: The square root of a fraction is the square root of the numerator divided by the square root of the denominator

√4.5 = √(9/2) = √9 / √2

Step 03: Simplify 9

3 / √2

Step 04: Rationalize the Denominator

(3 / √2) × (√2 / √2) = 3√2 / 2

The square root of 4.5 is 3√2 / 2. Since √2 is irrational, 4.5 is irrational.

What is 4 times the Square Root of 3

If you want to find 4√3, find the square root of 3, then multiply the value by 4.

Step 01: Write the expression

4√3

Step 02: Find the square root of 3

√3 is irrational, approximate value: √3 ≈ 1.732

Step 03: Multiply 4 by 1.732

4 × 1.732 = 6.928

So, 4√3 ≈ 6.928

What is 4 times the Square Root of 5

Step 01: Write the expression

4√5

Step 02: Find the square root of 5

√5 is irrational, approximate value: √5 ≈ 2.236

Step 03: Multiply 4 by 2.236

4 × 2.236 = 8.944

So, 4√5 ≈ 8.944

What is 4 times the Square Root of 81

Step 01: Write the expression

4√81

Step 02: Find the square root of 81

√81 = 9

Step 03: Multiply 4 by 9

4 × 9 = 36

So, 4√81 = 36, which is also a rational number.

What is the Square Root of 0.4

Step 01: Convert 0.4 into a fraction

0.4 = 4/10 = 2/5

Step 02: Apply the square root to the fraction

√(2/5) = √2 / √5

Both √2 and √5 are irrational, so 0.4 is also irrational.

Square Root of 3.4

Step 01: Write 3.4 as a fraction

3.4 = 34/10 = 17/5

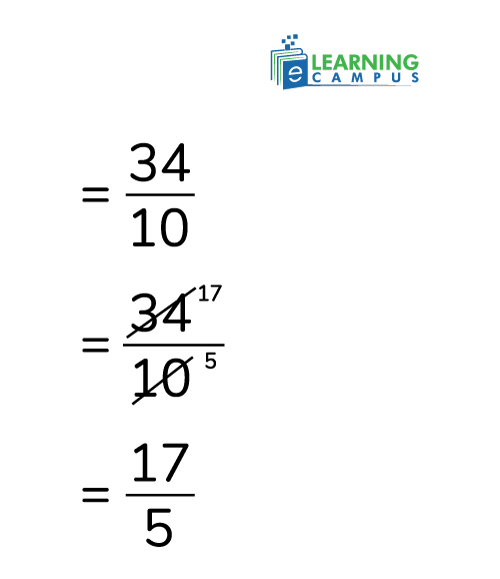
Step 02: The square root of a fraction is the square root of the numerator divided by the square root of the denominator

√(17/5) = √17 / √5

Step 03: Rationalize the Denominator

(√17 / √5) × (√5 / √5) = √85 / 5

Step 04: Optional Decimal approximation

√85 / 5 ≈ 9.220 / 5 ≈ 1.844

The square root of 3.4 is √85 / 5 ≈ 1.844. Since √85 is irrational, 3.4 is irrational.

What is the Square Root of 4 multiplied by 16

To find the square root of 4 multiplied by 16, first, multiply the values under the square root, then find the square root of the value. Here are the steps:

Step 01: Multiply values under the square root

4 × 16 = 64

So,

= 64

Step 02: Find the square root

As we know, 8 is the perfect square root of 64.

√64 = 8

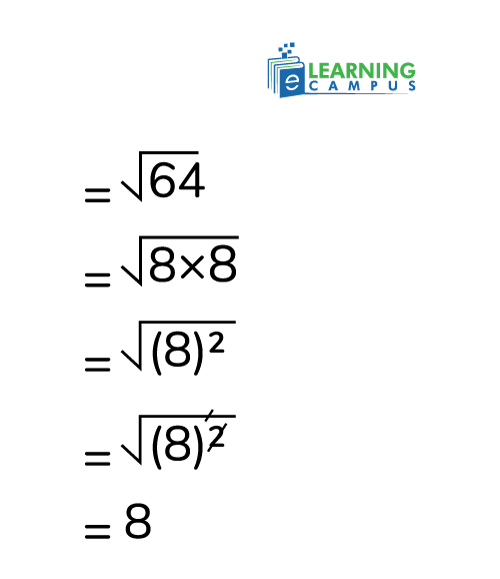
So, the square root of 4 multiplied by 16 is 8

Conclusions

The square root of a negative number might seem tricky at first, but with the imaginary unit (i) they become simple to handle. Remember,

√(-a) = √a · i, where a > 0

Understanding this concept is a key step in learning advanced mathematics and real-world applications.