Pythagorean Theorem Worksheet–Definition and Example

Pythagoras' theorem, also known as the Pythagorean theorem, has wide applications in Mathematics, including triangle measurements. Its importance stretches far beyond Math, expanding into the fields of physics, architecture, and engineering. The Pythagorean theorem worksheet will help you understand this theory and solve the related problems.

In this blog, you will learn about what the Pythagorean theorem states, its formula, and how to find the other side of a triangle if two sides are given.  

Pythagorean Theorem 

Pythagorean theorem is an important principle related to a right triangle. The right triangle has one angle equal to 90 degrees. The theorem states that;

“For any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides”. 

To understand the theorem better, let’s learn the key concepts used in this definition. 

• Hypotenuse: the side of the triangle that is opposite to the right angle (90 degrees). It is the longest of the other two sides of a triangle and is represented by ‘h’. 
• Base: The bottom line of any triangle is called base.
• Perpendicular: a line that make 90 degree 
• If a and b are two other sides, i.e. ‘a’ is perpendicular to the triangle and ‘b’ is the base, then the Pythagorean theorem can be written as;

Pythagoras Theorem Interpretation 

The Pythagorean theorem can be interpreted in many ways using geometry and algebra. This theorem can easily be interpreted by drawing a square with each side of a right triangle.

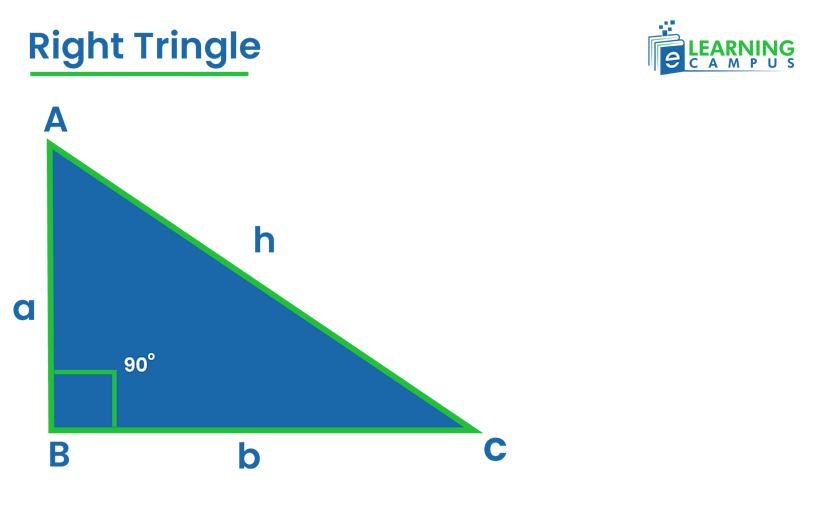
Let us consider a right triangle ABC, as shown in the figure below. In which;

• ‘AB’ is altitude.
• ‘BC’ is base 
• ‘CA’ is hypotenuse 

According to the theorem;

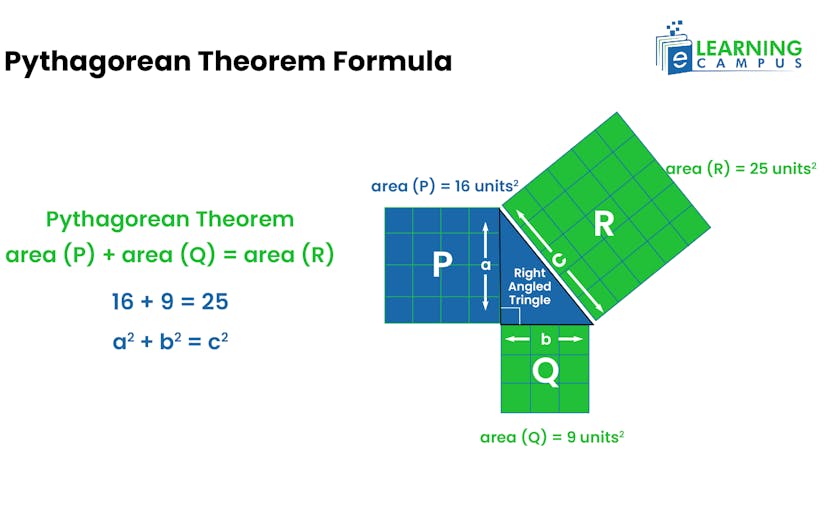
Now, we will draw a square on each side and name as P, Q, and R. According to the theorem, the sum of squares of areas of P and Q is equal to the square of the area of R. 

Let’s consider, the area of P is 4, the area of Q is 3, and the area of R is 5. 

Putting the values in the formula.

Geometric Proof Pythagorean Theorem

The Pythagorean theorem has been proved in many ways by different mathematicians. Let’s consider a Geometric proof of Pythagorean Theorem by using a square in a square approach. 

Let us draw a large square and an inner square in such a way that it forms four congruent right triangles at four edges. As shown in the figure.

In the above figure, four green triangles are congruent, in which;

• ‘a’ is altitude
• ‘b’ is a base
• ‘c’ is the hypotenuse

We know that in a right triangle, one side is of 90 degrees and the two other sides (acute angles) also make 90 degrees. 

In the above figure,

Let’s calculate it geometrically.

The length of the side of the outer square is

So, the area of the outer square will be

The length of the side of the inner square is c

So, the area of the inner square will be

The area of a triangle is

Now, we will calculate accordingly.

area of outer square= area of inner square+ area of 4 triangles.

By subtracting 2ab on both sides, we get,

Hence, we proved the Pythagorean theorem geometrically.

Pythagorean Theorem Word Problems

The word problems are the best way to understand the theorems. The Pythagorean Theorem word problems help understand the theorem and solve the problems. 

Let’s understand it by solving some Pythagorean Theorem practice problems. 

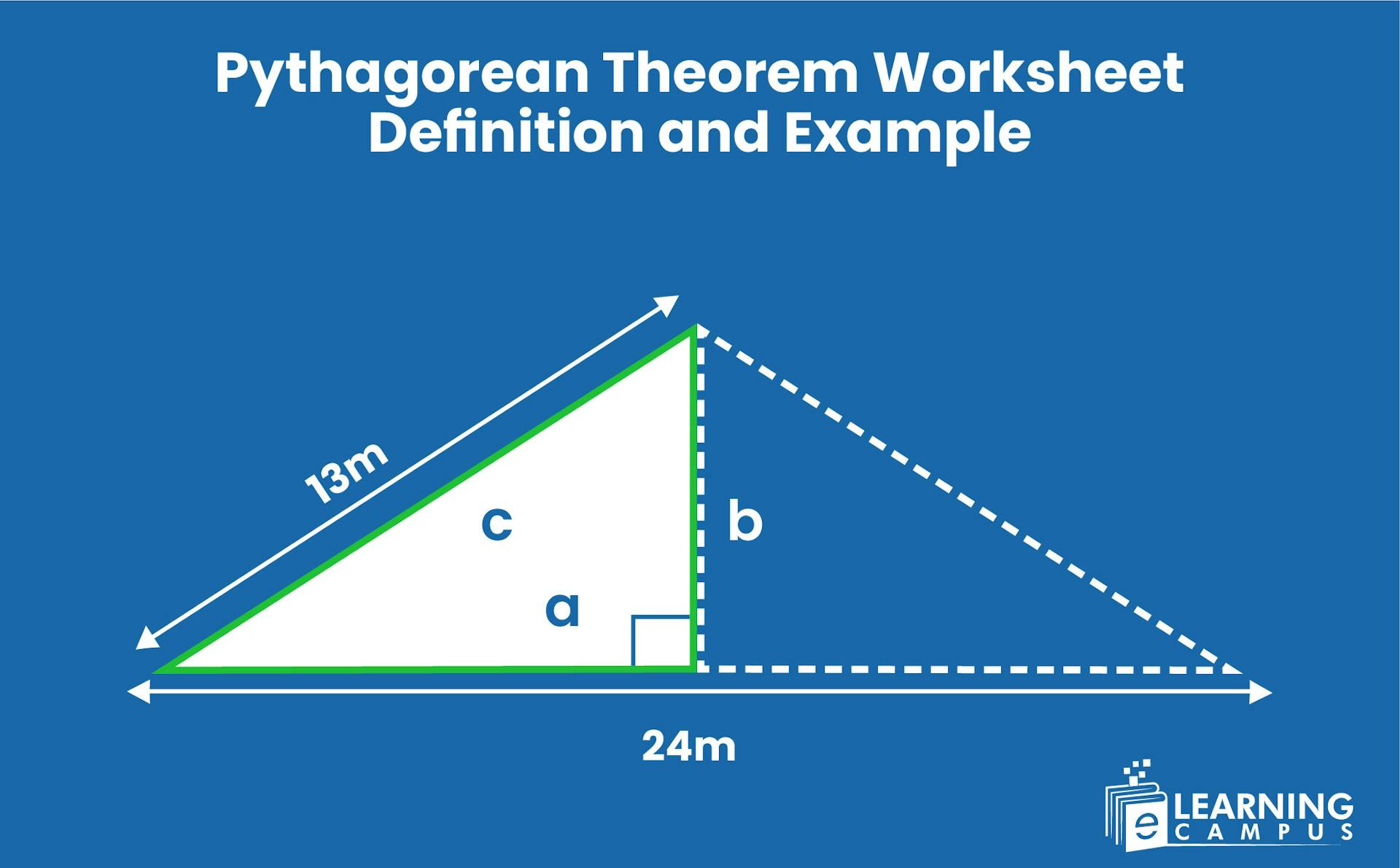
Example 1:

Find the hypotenuse of a triangle using Pythagoras’ theorem, in which the sides are 8 units and 6 units.

Pythagoras' theorem states that. 

Example 2

If the hypotenuse of a right triangle is 12 units, and one side is 8 units.  Find the length of the third side?

 In the above statement, 

Hypotenuse is 12 units. One side is 8 units. We consider it a base.

The theorem states that; 

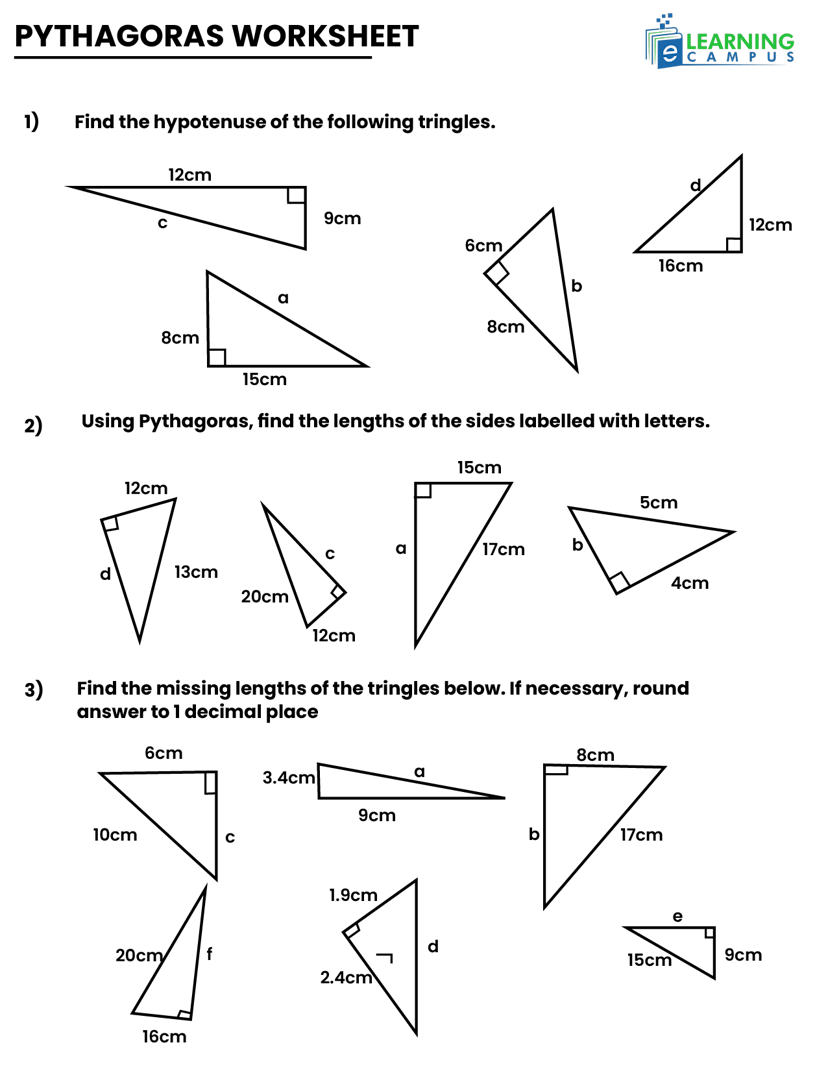
Pythagorean Theorem Practice Worksheet

Worksheets are beneficial in practicing the theorem-related problems. The Pythagorean theorem practice worksheet helps you understand the theorem by practicing the questions. 

Solve the problems given below and improve your mathematical skills.