Loading...
elearning Campus BlogLogarithms- Definition, Properties, and Rules
Logarithms- Definition, Properties, and Rules
Loading...
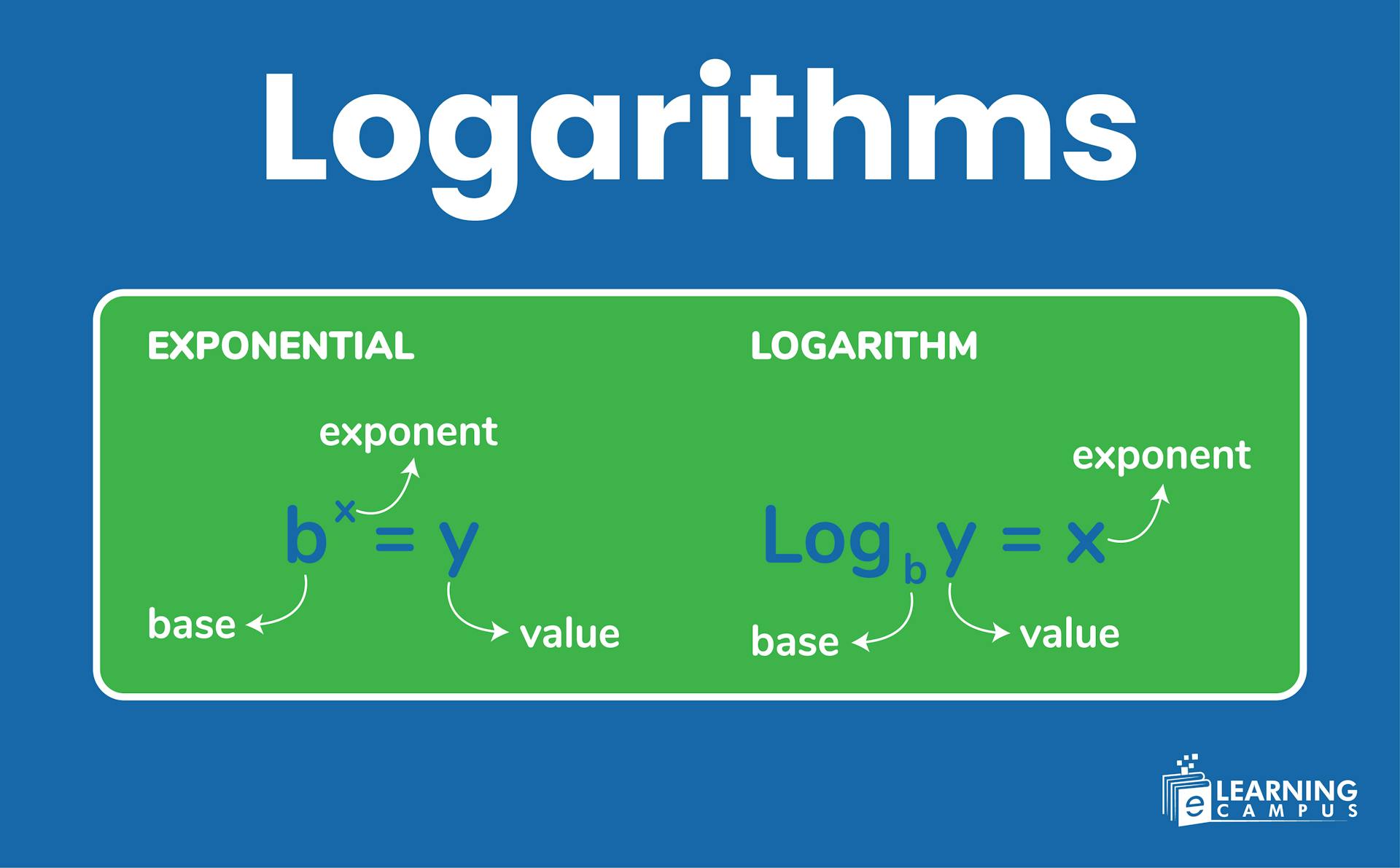
The logarithm is a quantity that represents the power to which a fixed number is raised to produce a given number. In Mathematics, logarithms are a unique way to express an exponential form of equation in a simple form. It can also be understood as the inverse operation of exponentiation.
In this blog, you will learn about logarithms in detail with the formula, rules, and properties.
Mathematics has unique inverse rules. Just as division is the inverse of multiplication, logarithms are the inverse of exponentiation. In simple terms, a logarithm answers the question, ‘To what power must a base number be raised to get a specific number?’
For example, if 2 raised to the power of 3, it equals 8, i.e, 2³ = 8, then the logarithm of 8 is 3, it will be expressed as;
log₂8 = 3
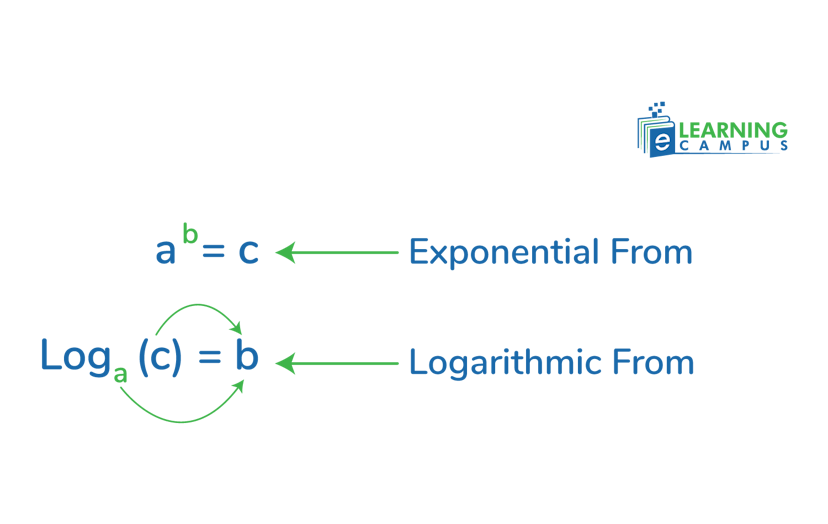
The logarithmic form is a rearrangement of an equation of exponential form. In this form, the same numbers are written in a different order. For the exponential form ab=c, the standard logarithmic form is expressed as;
To understand the concept of logarithms, we will learn the basic terms associated with this concept.
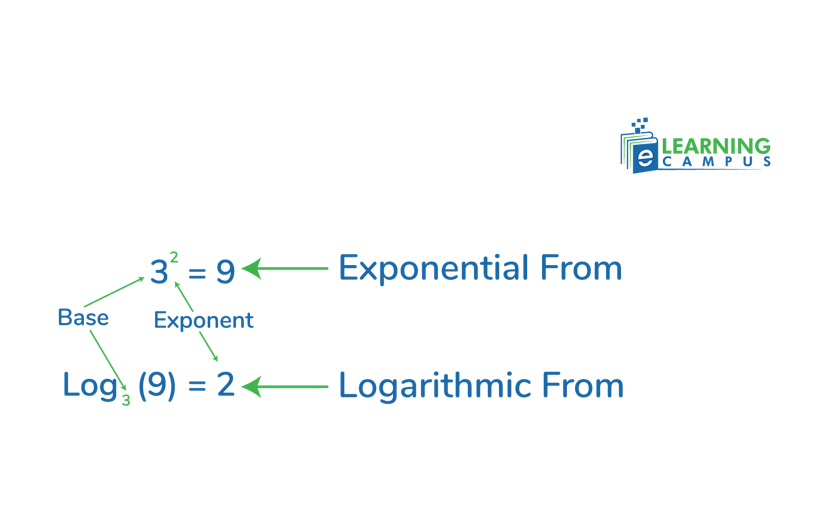
Let’s look at the example of how exponential form is written in logarithmic form.
We know that
The equation in the log form will be written as;
There are three main types of logarithms in Mathematics, namely the common logarithm, the natural logarithm, and the binary logarithm. Let’s discuss each in detail.
A common logarithm is also known as a decadic logarithm, decimal logarithm, or Briggsian logarithm. It is written with base 10.
It is often written as log(x), where x is the number whose logarithm is to be taken. A log without a base means it is log 10.
For example,
It means that if we multiply the number 10 three times, we get 1000. In logarhythmic form, it is expressed as;
The natural Logarithm is known as the base e logarithm. It is represented in the form;
In this log, ‘e’ represents Euler’s constant, whose value is equal to 2.71828.
Let’s look at the examples
A binary logarithm is the logarithm to the base 2 or log 2. It essentially inquires that "To what power must 2 be raised to obtain a certain number?" It is represented as;
or
$$ \log_b x $$
The logs possess certain properties that are based on the exponent rules. These properties are also known as the rule of logs. Let’s discuss each rule in detail.
The product rule of logs states that ‘the product of two logarithm values is equal to the sum of the individual logs. It is expressed as;
Example,
The logs’ division rule states that ‘the division value of two logs equals the difference between the two logarithmic values.
For example,
The exponential rule states that ‘ the log of m with an exponent that is a rational number is always equal to the exponent times of its logarithum.
Example,
The change of base rule for logarithms states that the logarithm of a number m to the base b can be expressed as the logarithm of m to a new base divided by the logarithm of b to the same new base a. It gives rise to logarithms of different bases.
Example,
A log with a value less than 1 is a negative log. To convert a negative log into a positive one, we need to take the reciprocal of it.
The value of log 1 is always zero, irrespective of base. We know that a0 = 1.
If we convert it into a log form, it will be expressed as;
Solving Word Problems Using Logarithms
As we have learned the logarithm in detail. Now we will solve the word problems using logarithms. Let’s look at some of the examples.
Example 1
If log 3 = 0.2010 and log 4 = 0.3771, then using the properties of log, find the value of log 36.
By using the product rule,
Putting the values of log 3 and log 4
Example 2
Find the value of x in
In exponential form, it can be written as;
Conclusion
Logarithms are an important concept in Mathematics. They are a unique way to write exponential form in its inverse. It helps to solve complex equations with exponents.
Are you struggling with mathematical concepts and want to learn them in a fun way? We are at your service. We have expert online math tutors who make math easy for you and your kids. You will be the math champion in less time.
