Line Perpendicular to Line

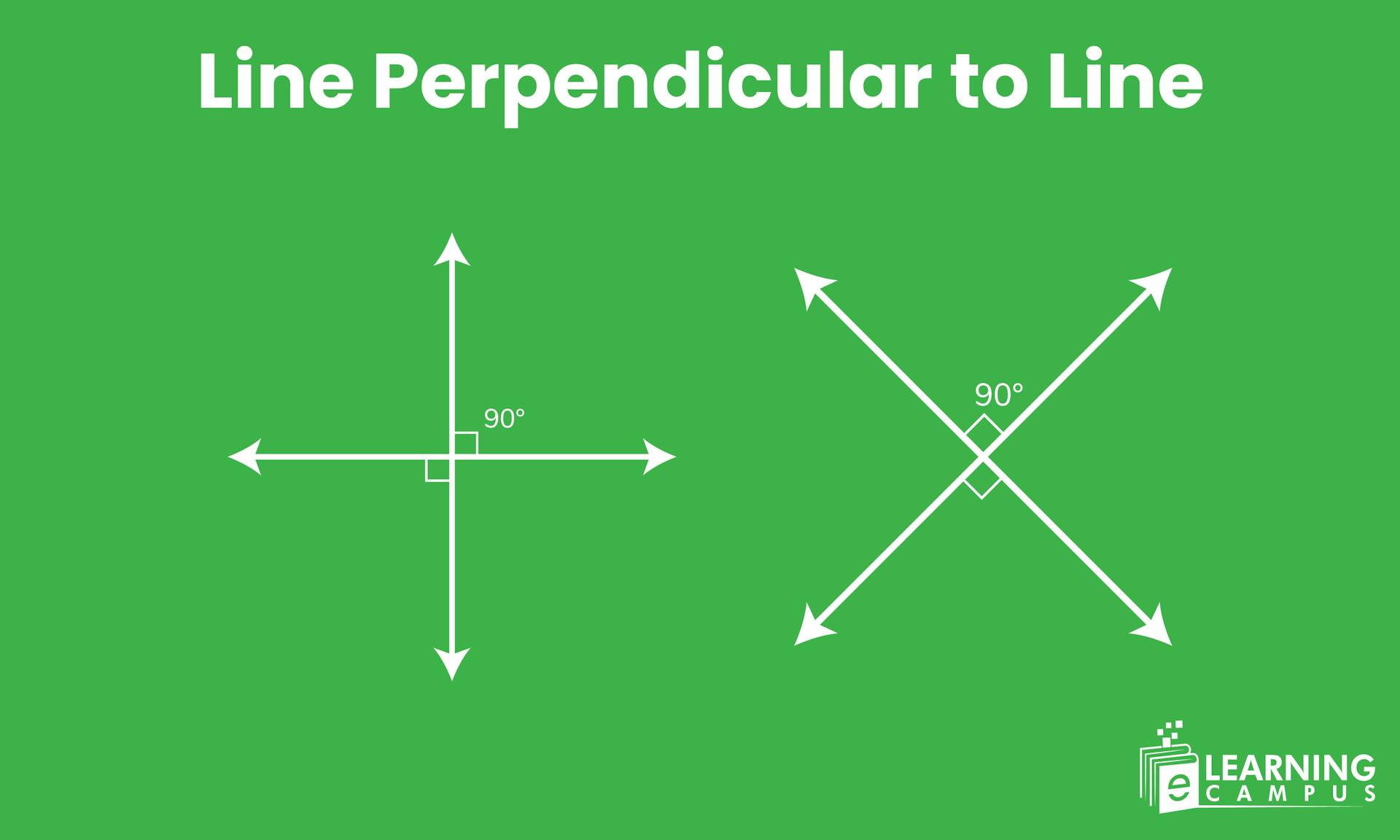
Do you know what makes a line perpendicular to another, and why this geometric relationship matters in math, engineering, or even art? A line becomes perpendicular to another when they intersect at a 90-degree angle. 

A line perpendicular to another line forms a right angle when it intersects. If the equation of the original line is known, we can find the equation of a perpendicular line.

In this blog, you will learn about how to determine perpendicular lines and the slope of a line perpendicular to a line. 

What are Perpendicular Lines

Perpendicular lines are two lines that intersect at a single point and form a perfect right angle. This relationship is represented by the symbol '⊥'. Common examples include the corner of a square or the way the walls of a room meet. 

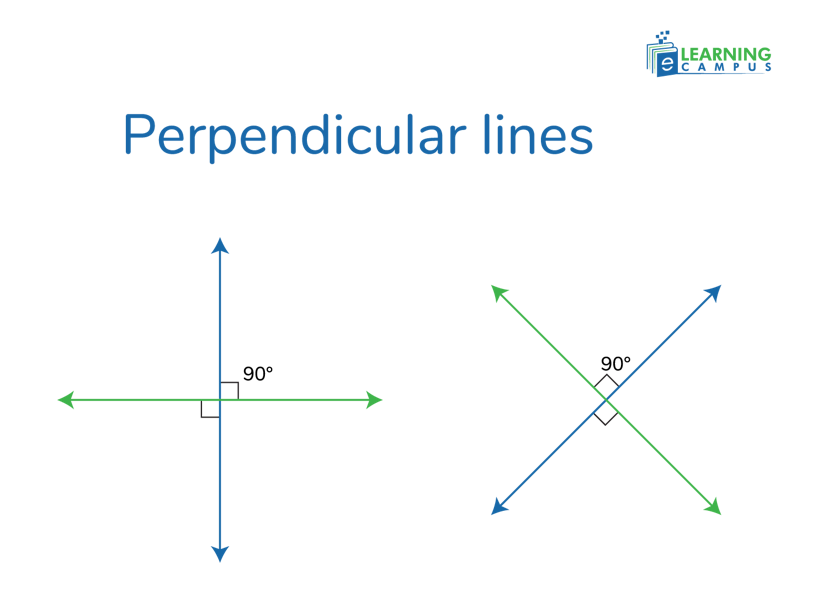
Line perpendicular to line example

A line perpendicular to another line intersects it at a 90° angle. It means their slopes are negative reciprocals of each other. For example, if one line has a slope of 2, the perpendicular line has a slope of −1/2. 

Real-world examples include the corners of a television or textbook, the arms of a clock at 3:00, or a street and the sidewalk it meets. 

Equation for Line Perpendicular

The equation for perpendicular lines is based on the relationship where their slopes are negative reciprocals of each other. If one line has a slope of m1, then the slope of the perpendicular line will be;

Slope of a Line Perpendicular to a Line

The slope of a line perpendicular to another line is the negative reciprocal of the original slope. For two non-vertical lines to be perpendicular, the slope of one line must be the negative reciprocal of the other. The product of their slopes is

How to Find the Slope of a Perpendicular Line

To find the slope of a perpendicular line, find the negative reciprocal of the original slope. Then, flipping the original slope's fraction and changing its sign.

Steps to find the perpendicular slope

• Find the original slope

If an equation is given, rearrange it into slope-intercept form y=mx+b to find the slope m.

If you have two points, use the slope formula:

•  Find the reciprocal 

Flip the fraction so the numerator becomes the denominator and vice versa. 

• Change the sign.

Multiply the reciprocal by -1 to find the negative reciprocal. If the original slope was positive, the new slope is negative. If the original was negative, the new slope is positive. 

Example 1: If two points are given

Find the Slope of the line Perpendicular to the line through the two Points (2, 3), (4, 7)

As two points are given, we will use the formula to find the slope 

Substitute the value of x and y

Now find the negative reciprocal. The slope of the original line is 𝑚. The slope of the perpendicular line will be

To find the negative reciprocal, flip the fraction. If your original slope is a whole number, write it as a fraction. In this case, we have 2. We will write it as

Now, flip the fraction

Change the sign: Since the original slope was positive, the new slope is negative. The slope of the perpendicular line is

Example 2: if the equation is in slope-intercept form

Find the slope of a line perpendicular to 𝑦=3𝑥−2

The equation is in slope-intercept form. So, the slope m=3. 

Now, take the reciprocal 3, which is

Change the sign. The negative reciprocal is

How to Determine if Lines are Perpendicular

There are several methods to determine if the lines are perpendicular. We can determine that two lines are perpendicular if their slopes are opposite reciprocals of each other. 

Method 1: Multiply the slopes 

• Find the slope of each line m1 and m2. 
• Multiply the two slopes together m1 x m2
• If the product equals −1, the lines are perpendicular. 

Method 2: Use a protractor (geometric)

If we have a diagram of the two intersecting lines, we can use a protractor to measure the angle they form. 

• Place the protractor's center point on the intersection of the two lines.
• Align the protractor's baseline with one of the lines.
• Read the measurement where the second line crosses the protractor's scale.
• If the angle is exactly 90°, the lines are perpendicular. A small square is often used to mark a right angle in diagrams.

Special case of Vertical and horizontal lines

A vertical line has an undefined slope, and a horizontal line has a slope of 0. If one line is horizontal and the other is vertical, they are perpendicular to each other

Conclusion 

A line perpendicular to another line is a line that intersects it at a right angle (90∘). The slopes of two perpendicular lines are negative reciprocals of each other. It means if one line has a slope of m, the perpendicular line's slope is -1/m.