elearning BlogLeast Common Multiple Problems

Least Common Multiple Problems

Least common multiple problems using division and factorization methods

Are you struggling with the Least Common Multiple problems and finding no way to solve them? Have patience. Let’s help you solve the problems on LCM quickly. 

In this blog, you will learn about LCM (lowest common multiple) and will get tips to solve the Lowest Common Multiple problems using different methods. 

Let’s learn what LCM is.

Lowest Common Multiple (LCM)  

LCM, or the least common multiple of two or more than two numbers, is the least single value that is common among all multiples of the given numbers and divisible by all the numbers. 

We will understand it with the help of examples.

Example:

Let us consider two numbers, 3 and 5.

First, we will see the multiples of both numbers and then find the LCM.

Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30………

Multiples of 5 are 5, 10, 15, 20, 25, 30, 35……..

Now, see which number is common in the multiples of both. We can see that 15 and 30 is common in both multiples.

15 is less than 30. Therefore, 15 is the lowest common multiple of 15 and 30. 

We can write it as LCM (3,5)= 15

Methods to Find LCM 

Three different methods are used to find the LCM of numbers, including the Listing Method, the Prime Factorization Method, and the Division Method. We will learn each method in detail with examples.

LCM by Listing Method 

In the listing method of LCM, we calculate the lowest Common multiple by listing the multiples of numbers and picking the least common number.

Let’s understand it with an example.   

Consider we have two numbers, 2 and 9. We will find LCM of 2, 9 using the listing method. 

First, we will find the multiples of 2 and 9

  • Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…….. 
  • Multiples of 9: 9, 18, 27, 36, 45, ………

Now, choose the smallest value that is common in both multiples. 

We can see that 18 is the smallest common number. 

So,LCM(2,9)=18\textbf{So,} \quad LCM(2, 9) = 18
LCM of 2 and 9 commons multiples

LCM by Division Method 

The division method is the simplest and most commonly used method of calculating the lowest common multiple.  In this method, we divide the numbers by the smallest prime number and move on dividing until we get one at the end. 

Let’s understand it with the help of an example. 

Example: 

Consider we have two numbers, 6 and 20. We will find the LCM using the division method. 

  1. We will choose a prime number that is a multiple of both or one number. 
  2. 2 is the least prime number that is a factor of 6 and 20. Divide 6 and 20 by 2. On division, we are left with 3 and 10.
  3. Divide the numbers again by 2 because 10 is still divisible by 2, and write three below as it is.
  4. Now divide the numbers by 3. We are left with 1 and 5.
  5. Divide by 5. Now, we have one on both columns. 
  6. Multiply the numbers on the left. 
2×2×3×5=602 \times 2 \times 3 \times 5 = 60
  1. We have calculated the LCM of 6 and 20. 
So,LCM(6,20)=60\textbf{So,} \quad LCM(6, 20) = 60
LCM of 6 and 20 using division method

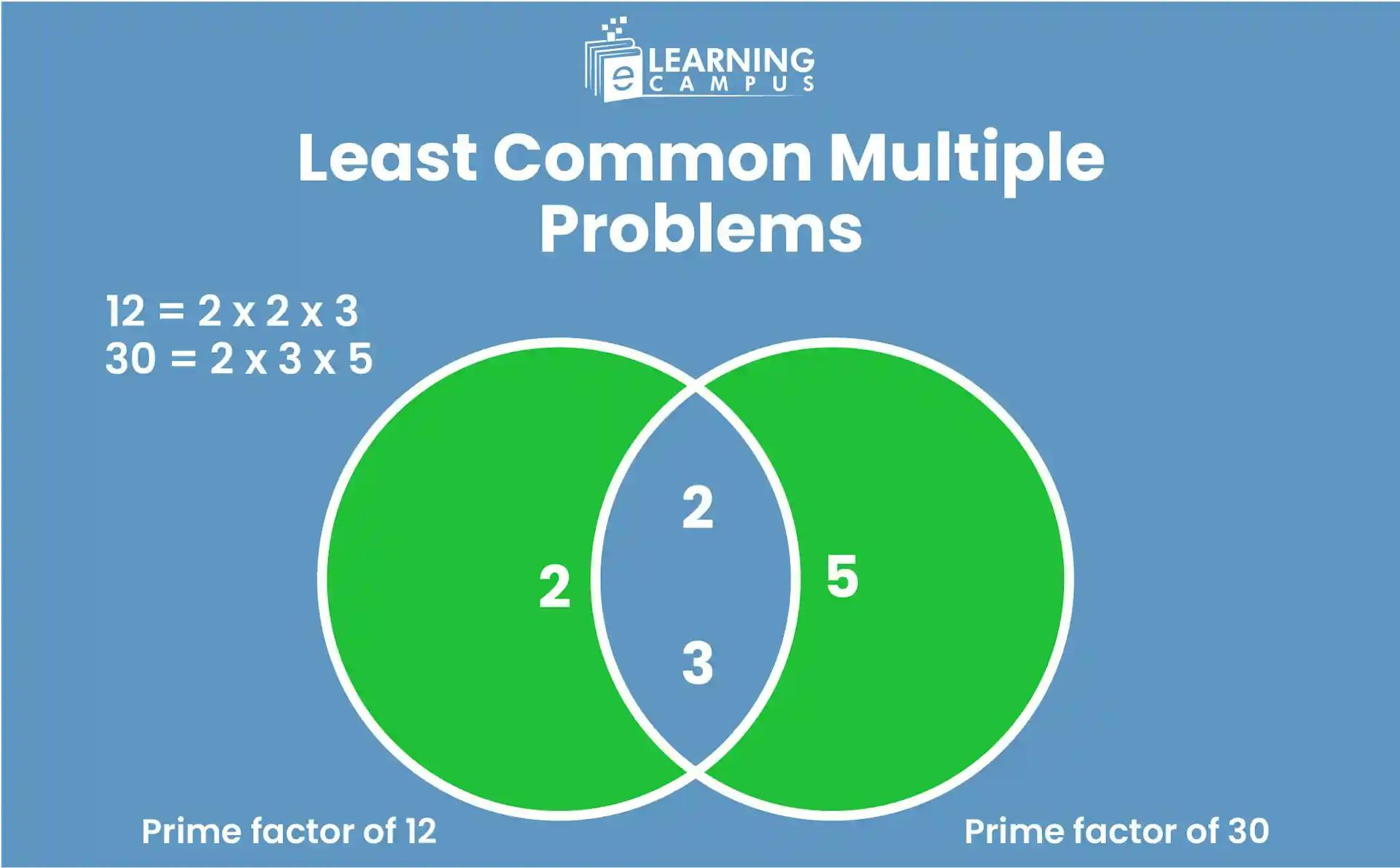
LCM by Prime Factorization Method 

Prime factorization is a method of calculating the least common multiple of numbers by finding the prime factors of numbers and writing them in exponential form. On multiplication, we can achieve the LCM of desired numbers. 

Let’s understand it through example. 

Example:

Suppose we have two numbers, 80 and 120. To find the LCM, we will follow these steps.

  1. We will find the prime factors of the 80 and 120 by the repeated division method.
Division method to find LCM of 80 nf 20 i.e 240
  1. The prime factor of 80 is
2×2×2×2×52 \times 2 \times 2 \times 2 \times 5

The prime factor of 120 is

2×2×2×3×52 \times 2 \times 2 \times 3 \times 5
  1. Now, we will write the prime factors in exponential form.
80=24×5180 = 2^4 \times 5^1
120=23×31×51120 = 2^3 \times 3^1 \times 5^1
  1. Now, we will write the factors with the highest exponent. 
24×31×512^4 \times 3^1 \times 5^1
  1. Now multiply these numbers accordingly.
16×3×5=24016 \times 3 \times 5 = 240

So, the LCM of 80 and 120 is 240. 

Find the LCM of Fractions

The LCM of fractions can be calculated by finding the LCM of numerators and dividing it by the HCF of denominators.

The formula to find the LCM of fractions is;

LCM=LCM of NumeratorHCF of DenominatorLCM = \frac{\textit{LCM of Numerator}}{\textit{HCF of Denominator}}

Let’s learn how to find LCM of fractions using the formula. 

We will understand it through examples. 

Example:

Suppose we have two fractions

1236and924\frac{12}{36} \quad \text{and} \quad \frac{9}{24}

We will find the LCM using the formula.

  1. First, calculate the LCM of numerators i.e. 12 and 9 with anyone of above mentioned methods. The LCM of 12 and 9 is 36. 
  2. Find the highest common factor of denominators i.e. 36 and 24. The calculated HCF of 36 and 24 is 12. 
  3. Put the values in the formula.
LCM=LCM of NumeratorHCF of DenominatorLCM = \frac{\textit{LCM of Numerator}}{\textit{HCF of Denominator}}
LCM=3612=3LCM = \frac{36}{12} = 3
So, the LCM of 1236 and 924 is 3.\textbf{So, the LCM of } \frac{12}{36} \textbf{ and } \frac{9}{24} \textbf{ is } \mathbf{3}.

Solving the Lowest Common Multiple Problems

As we learned about LCM and methods to find the LCM, now we will solve different lowest common multiple problems using each method.  

  1. Find the LCM of 15 and 18 by the listing method. 

To find the least common multiple of 15 and 18, we will follow the following steps.

  •  Find the multiple of 15 and 18 respectively. 
15=15,30,45,60,75,90,105,…15 = 15, 30, 45, 60, 75, 90, 105, \dots
18=18,36,56,72,90,108,…18 = 18, 36, 56, 72, 90, 108, \dots
  • Choose the least common number.
  • 90 is the smallest common number among the multiples of 15 and 18.

$$ \textbf{So,} \quad LCM(15, 18) = 90 $$
Find the LCM of 14, 26, 66 using the division method.

LCM of 14, 26 and 66
  1. Find the LCM of 1200 and 800 by the prime factorization method.  
  • To find the lowest common multiple of 16 and 20, we will find the prime factor of 1200 and 800 separately by the repeated division method.
LCM of 1200 and 800 by division methods
  • Now, write the factors in exponential form.
1200=2×2×2×2×3×5×51200 = 2 \times 2 \times 2 \times 2 \times 3 \times 5 \times 5
24×31×522^4 \times 3^1 \times 5^2
800=2×2×2×2×2×5×5800 = 2 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5
25×522^5 \times 5^2
  • Write the value with the highest power.
25×31×522^5 \times 3^1 \times 5^2
32×3×25=240032 \times 3 \times 25 = 2400
So, the LCM(1200,800)=2400\textbf{So, the } LCM(1200, 800) = 2400

Learn Math with Expert Online

Are you looking for an expert online Math tutor to teach your kids? We have professional teachers to make Math interesting for your kids.

Hire a maths tutor to learn maths problems
Hire a Tutor Now

FAQs