elearning BlogKinematic Equations

Kinematic Equations

Kinematic Equations

Kinematic equations are a set of equations in physics that describe the motion of objects, specifically relating displacement, velocity, acceleration, and time, when the acceleration is constant. These physics formulas are used to determine unknown aspects of an object's motion when other aspects are known. 

What are the Kinematic Equations?

The kinematics in physics is the study of how objects move, without considering the forces that cause them. In simple terms, kinematics deals with the motion of objects, not the cause of that motion (force). So, the kinematic equations are the mathematical representation of the motion of objects without focusing on the cause of motion. 

All kinematic equations deal with the following kinematic variables;

  • Displacement ( Δx)
  • Initial Velocity (v0)
  • Final Velocity (v)
  • Time interval ( t)
  • Constant acceleration (a)

The 4 Kinematic Equations

There are 4 kinematic equations. These equations apply to the motion of a body with constant velocity or acceleration. They can never be used over any period in which the acceleration is changing. The four kinematic equations are given as; 

v=v0+atv = v_0 + at
△x=(v+v02)t\triangle x = \left( \frac{v + v_0}{2} \right)t
△x=v0t+12at2\triangle x = v_0 t + \frac{1}{2} a t^2
v2=v02+2aΔxv^2 = v_0^2 + 2a \Delta x

Each of the kinematic equations includes four different variables. If the values of three variables are given, we can calculate the value of the fourth variable. 

These 4 equations of kinematics are known as the first, second, third, and fourth kinematic equations. 

Let’s discuss all kinematic equations in detail. 

First Kinematic Equation 

The first kinematic equation describes the relationship between an object's final velocity (v), initial velocity (v0), acceleration (a), and time (t). It states that “the final velocity of an object is equal to the sum of its initial velocity and the product of acceleration and time.” Mathematically, it is written as;

v=v0+atv = v_0 + at

It means that if we have a constant acceleration of an object for some time, we can find the final velocity of that object. 

Second Kinematic Equation

The second kinematic equation states that “displacement is equal to the product of the time and final velocity plus initial velocity divided by two.”

△x=(v+v02)t\triangle x = \left( \frac{v + v_0}{2} \right)t

3rd Kinematic Equation

The 3rd kinematic equation describes the displacement (distance) of an object moving with constant acceleration, relating it to its initial velocity, time, and acceleration. This equation states that “displacement is equal to the product of  initial velocity and time plus one-half acceleration times time squared.” It is represented as;

△x=v0t+12at2\triangle x = v_0 t + \frac{1}{2} a t^2

4th Kinematic Equation

The 4th kinematic equation relates final velocity (v), initial velocity (v₀), acceleration (a), and displacement (Δx) without requiring time. It is particularly useful when acceleration is known and one wants to determine final velocity or displacement. The fourth kinematic equation states that “the square of the final velocity is equal to the square of the initial velocity plus two times the product of acceleration and displacement”.

v2=v02+2aΔxv^2 = v_0^2 + 2a \Delta x

Derivation of Kinematic Equations

Kinematics deals with the motion of an object with constant acceleration. We learned about the kinematic equations, now we will learn how to derive the kinematic equations. 

For the derivation of kinematic equations, first, we need to understand the definition of the kinematic variables. 

Derivation of the first kinematic equation

To derive the first kinematic equation, we should begin with the definition of acceleration,

a=ΔvΔta = \frac{\Delta v}{\Delta t}

v is the change of velocity. 

a=vi−v0Δta = \frac{v_i - v_0}{\Delta t}
v=v0+aΔtv = v_0 + a \Delta t
v=v0+atv = v_0 + a t

So, we derive the first equation of kinematics from acceleration. 

Derivation of the second kinematic equation

To derive the second kinematic equation, consider a velocity and time graph with constant acceleration shown below. The velocity graph slope is interpreted as an acceleration, and the area under the graph is the displacement of the object.   

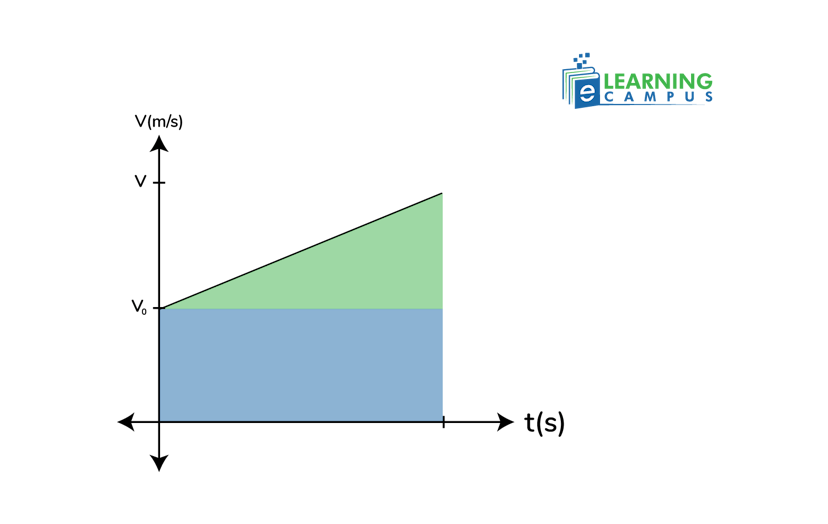
Derivation of the second kinematic equation

The height of the green rectangle is v0 and the width is 𝑡, so the area is v0t. 

The base of the blue triangle is ‘t’, and the height is v-vo. So, the area of the blue triangle is

x=12t(v+v0)x = \frac{1}{2} t (v + v_0)

The addition of blue and green areas gives

Δx=v0t+12t(v−v0)\Delta x = v_0 t + \frac{1}{2} t (v - v_0)
Δx=v0t+12vt+12v0t\Delta x = v_0 t + \frac{1}{2} v t + \frac{1}{2} v_0 t

By simplifying the equation 

Δx=v0t+12at2\Delta x = v_0 t + \frac{1}{2} a t^2

On further simplification, we get the 2nd equation of kinematics. 

Δx=(v+v02)t\Delta x = \left(\frac{v + v_0}{2}\right) t

Derivation of the third kinematic equation

We can derive the third kinematic equation with the help of the first and second kinematic equations. Starting with the 2nd kinematic equation,

Δx=(v+v02)t\Delta x = \left(\frac{v + v_0}{2}\right) t
Δxt=v+v02\frac{\Delta x}{t} = \frac{v + v_0}{2}

Substituting the value of ‘v’ from the first equation, i.e,  v = v₀ + at .

Δxt=v+v02\frac{\Delta x}{t} = \frac{v + v_0}{2}
Δxt=(v0+at)+v02\frac{\Delta x}{t} = \frac{(v_0 + at) + v_0}{2}
Δxt=v02+at2+v02\Delta x t = \frac{v_0}{2} + \frac{a t}{2} + \frac{v_0}{2}

Simplify the equation.

Δxt=v0+at2\frac{\Delta x}{t} = v_0 + \frac{a t}{2}

Multiplying both sides by ‘t’ 

Δx=v0t+12at2\Delta x = v_0 t + \frac{1}{2} a t^2
Δx=tv0+12at2\Delta x = t v_0 + \frac{1}{2} a t^2
Δx=v0t+12at2\Delta x = v_0 t + \frac{1}{2} a t^2

Hence, the third kinematic equation is proved.

Derivation of the fourth kinematic equation

To derive the fourth kinematic equation, we will take the first and second equations into account. To begin with, the second kinematic equation,

Δx=(v+v02)t\Delta x = \left(\frac{v + v_0}{2}\right) t

Substituting the value of t from the first equation,

v=v0+atv = v_0 + at
t=v−v0at = \frac{v - v_0}{a}

Combining the first and second kinematic equations formula

Δx=(v+v02)(v−v0a)\Delta x = \left( \frac{v + v_0}{2} \right) \left( \frac{v - v_0}{a} \right)

Simplifying the equation,

Δx=v2−v022a\Delta x = \frac{v^2 - v_0^2}{2a}

Further simplifying the equation,

2aΔx=v2−v022 a \Delta x = v^2 - v_0^2
v2=v02+2aΔxv^2 = v_0^2 + 2a \Delta x

So, we derived the fourth kinematic equation.

Conclusion 

Kinematic equations are a set of mathematical equations used to describe the motion of an object, specifically when the acceleration is constant. They relate displacement, initial and final velocities, acceleration, and time. These equations are essential for analyzing motion in a variety of scenarios, from simple projectile motion to more complex systems. 

Learn Physics with Expert online tutors

Are you looking to learn physics with expert tutors while sitting at home? We got you covered. We have expert teachers to teach you physics according to your needs and motivate you to achieve your goals. 

Learn Physics with Expert online tutors
Get started

FAQs