How to Find Surface Area
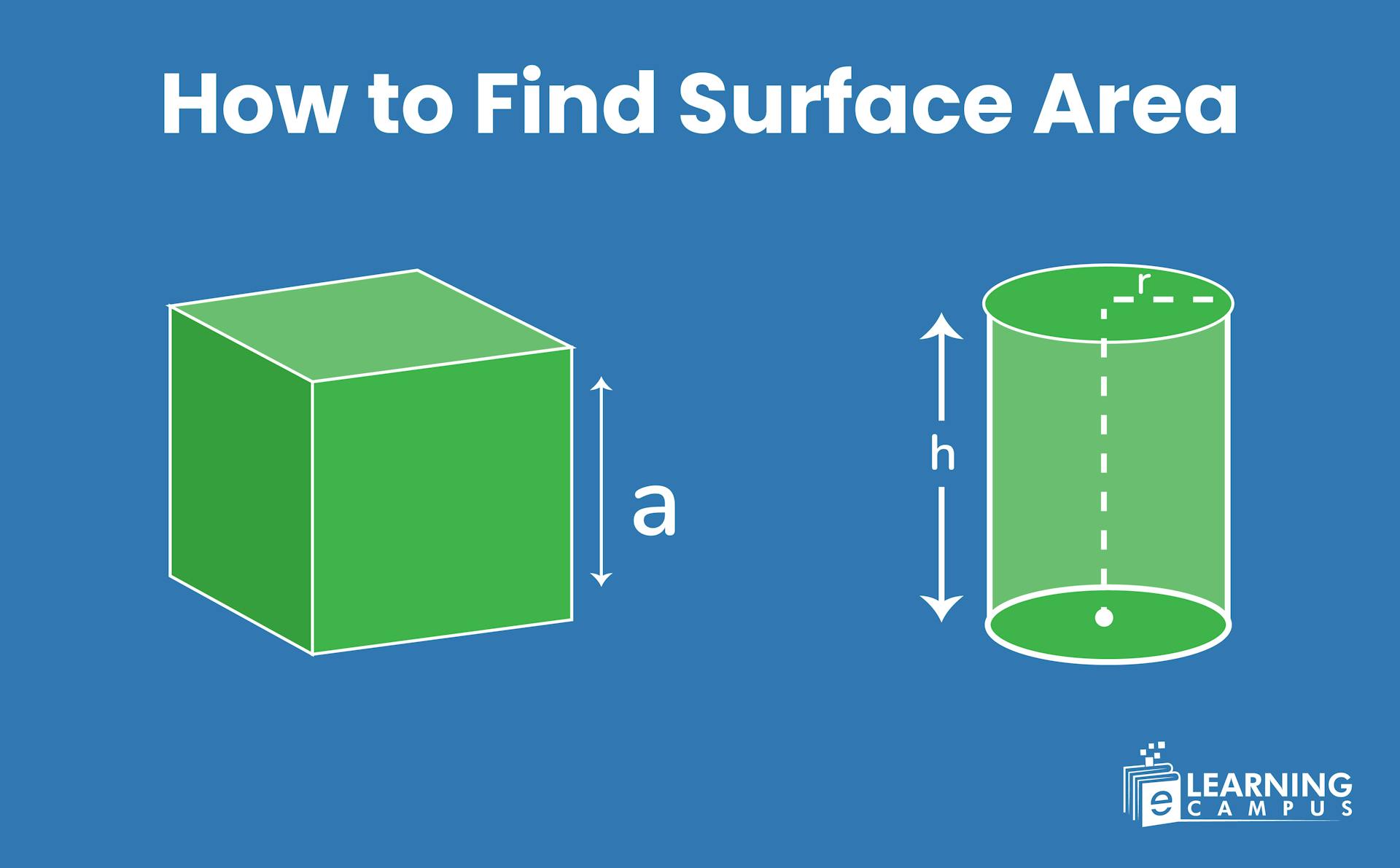
Have you ever noticed that the objects we deal with every day have different shapes and structures? You may be thinking about how to find surface area of objects with different shapes. We will help you with this phenomenon.
In this blog, you will learn about the surface area, the area of a surface formula, and how to calculate surface area of different 3d geometric shapes.
What is the Surface Area
Before proceeding to the geometric calculation, let’s first understand what is the surface area. Surface area can be defined as the total area or space a specific object occupies. Every geometrical shape has a different area of surface and can easily be calculated by the formula for surface area.
How to Calculate Surface Area
The surface area of all geometrical shapes is the sum of the area of all the faces of the object. To calculate total surface area, we find the area of each face and sum them up. The following steps are involved in finding the surface area;
- Identify 2-dimensional faces of the object.
- Calculate the area of each two-dimensional face.
- Add the calculated areas together.
- Write the units along the answer.
Surface Area Formulas
Formulas are the mathematical representation of the area of an object. In geometry, the total surface area of objects with different shapes and structures can be calculated by using surface area formulas.
These formulas help us to calculate the surface area of 3d shapes of all types, either flat or curved.
You will learn how to find the surface area using the formula.
Surface Area Units
Surface area units are the units that are used to measure the total surface area of the 3-dimensional objects. The surface areas are 2-dimensional, therefore, area is measured in square units such as Square millimeters (mm²),
Square centimeters (cm²), Square meters (m²), Square inches (in²), Square feet (ft²).
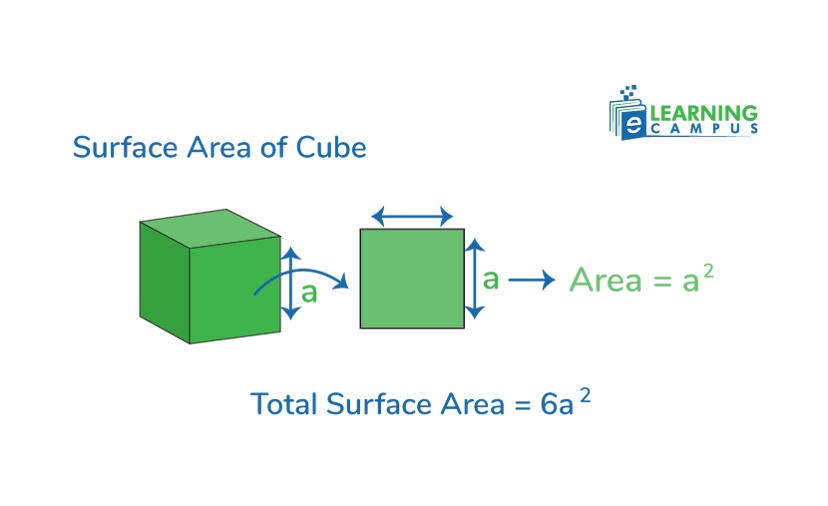
The Surface Area of a Cube
A cube is a 3-dimensional object with six equal and square faces. To find the surface area of a cube, we first find the area of one side and multiply it by 6
So, the surface area formula for cube will be,
Cube=6a2
Where,
- a2 is the area of one side
- 6 represents the 6 equal sides of a cube.
The unit of measurement for surface area of the cube is expressed in square units. I.e, square centimeters (cm²), square meters (m²), or square inches (in²).
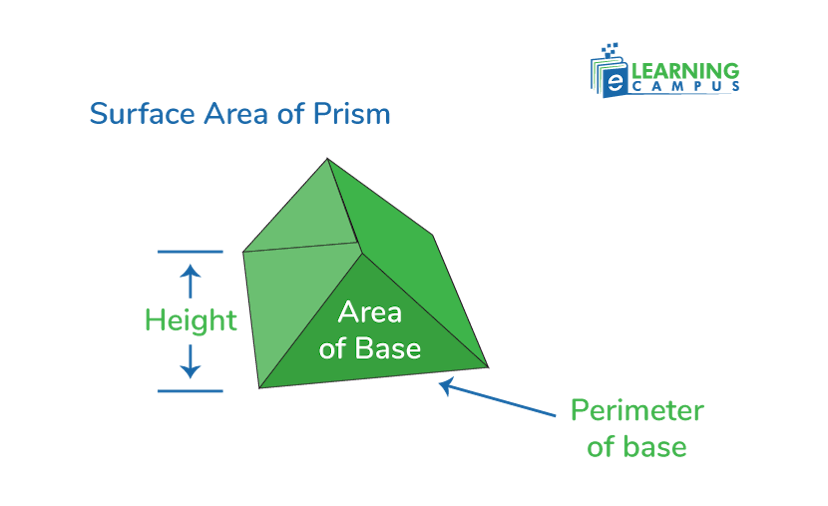
The Surface Area of a Prism
A prism is a 3-dimensional solid that has identical faces on opposite sides. The surface area of a prism is the sum of all the faces.
The formula to find the surface area of a prism is given by as;
Where,
- b is the base area of prism.
- p is the prism’s base parameter.
- h is the height of the prism.
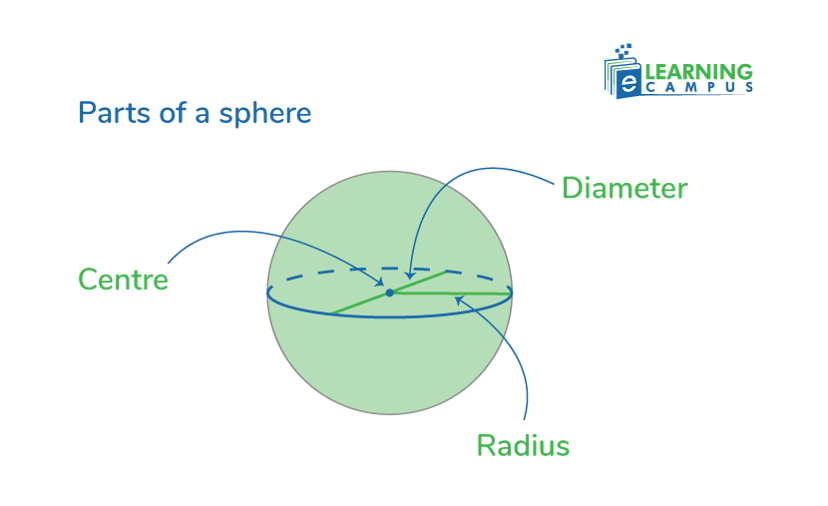
The Surface Area of a Sphere
A sphere is a 3-dimensional solid, in which every point on the surface is at an equal distance from a center point. It has no vertices or edges.
The surface area of a sphere is the calculation of the outer curved area.
The formula to find the sphere’s surface area is;
Where, r is the radius of the sphere.
Square units, e.g., m², cm², in², ft², are surface area unit of measure for the sphere.
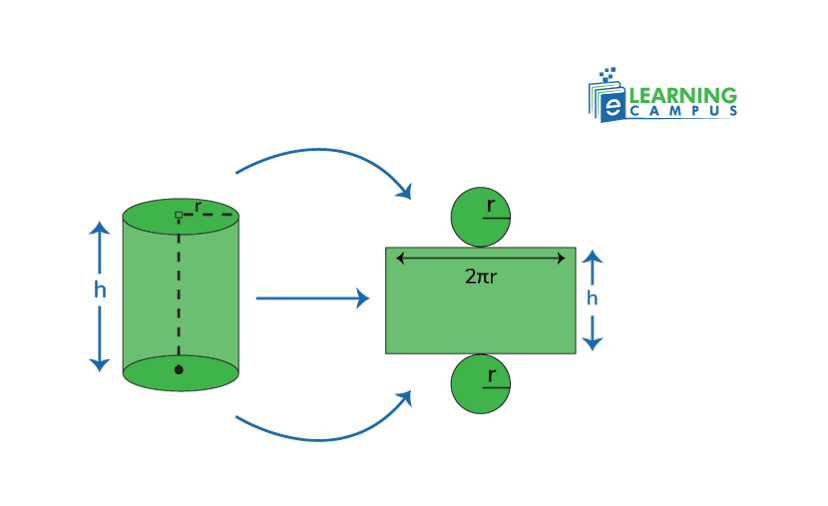
The Surface Area of Cylinder
The cylinder is a 3-dimensional object made up of two equal and circular faces and a curved body. The curved body, when flattened, becomes a rectangle.
The formula to find the surface area of the cylinder is given as;
In which,
- A represents the surface area.
- r is the radius of the circular face.
- h is the height of a curved surface.
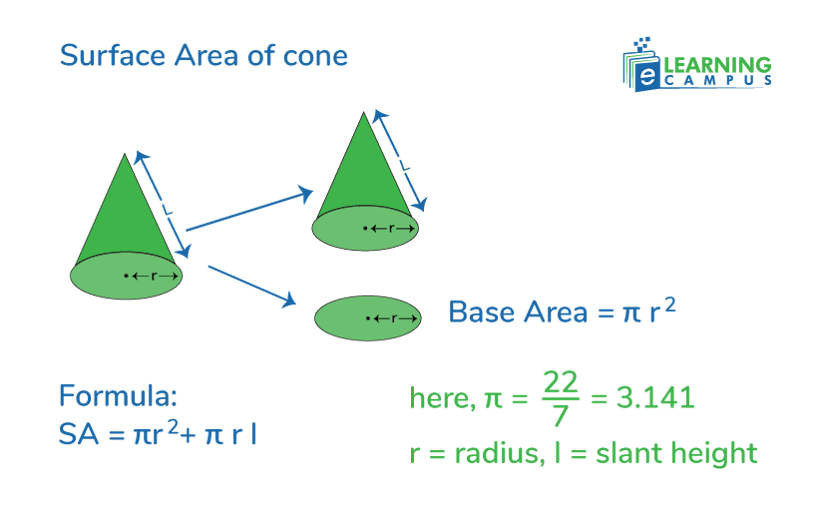
The Surface Area of Cone
The cone is a 3-dimensional figure, made up of a circular and flat base and a curved surface that is extended toward the top.
The formula to find the surface area of a cone is given as;
Where,
- π=3.14
- r is the radius of the base area.
- l is slant height.
The surface area measurement of the cone is expressed in square units such as cm2, m2.
Get Expert Tutor for Math
Are you looking to hire an online math tutor for your kids? You are at the right place. We have professional math teachers to ignite your future Mathematician.
