elearning BlogHow to Calculate the Slope of a Line

How to Calculate the Slope of a Line

How to Calculate the Slope of a Line – Explained 

Do you struggle with calculating the slope of a line or wonder how to measure the steepness of a hill or predict the trajectory of a rocket? It is all related to one simple concept, the slope of a line. 

If you don’t know how to calculate the slope of a line, this guide will break down this fundamental concept with clear, step-by-step guidance and practical examples. 

What Is the Slope of a Line

The slope of a line is the measurement of its steepness. It shows the rate of change of the vertical value compared to the horizontal value. A steeper line has a larger slope, indicating a greater rate of change between the vertical and horizontal quantities, while the slope of a flatter line is smaller. 

How to Calculate the Slope of a Line With Two Points

To calculate the slope of a line with two points, we use the slope formula. The slope formula shows the change in the y-coordinates divided by the change in the x-coordinates. It is given as;

m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}

Calculating the slope with two points involves these steps; 

  • Identifying the two points
  • Apply the formula
  • Calculate the changes
  • Divide to find the slope

Example

Find the slope of the line that passes through the points (1, 2) and (3, 6). 

  • Points: (x₁, y₁) = (1, 2) and (x₂, y₂) = (3, 6).
  • Formula:
m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}
  • Calculate changes:
m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}
m=6−23−1m = \frac{6 - 2}{3 - 1}
m=42m = \frac{4}{2}
  • Divide: m = 4 / 2
  • Simplify: m = 2

How to Calculate the Slope of a Line on a Graph

 The slope of a line on a graph can be found by finding two points on the line, calculating the change in y-values (rise) and the change in x-values (run) between them. Then, dividing the rise by the run using the formula. 

Example 

Consider that we have a graph with a slope as shown in the diagram.  

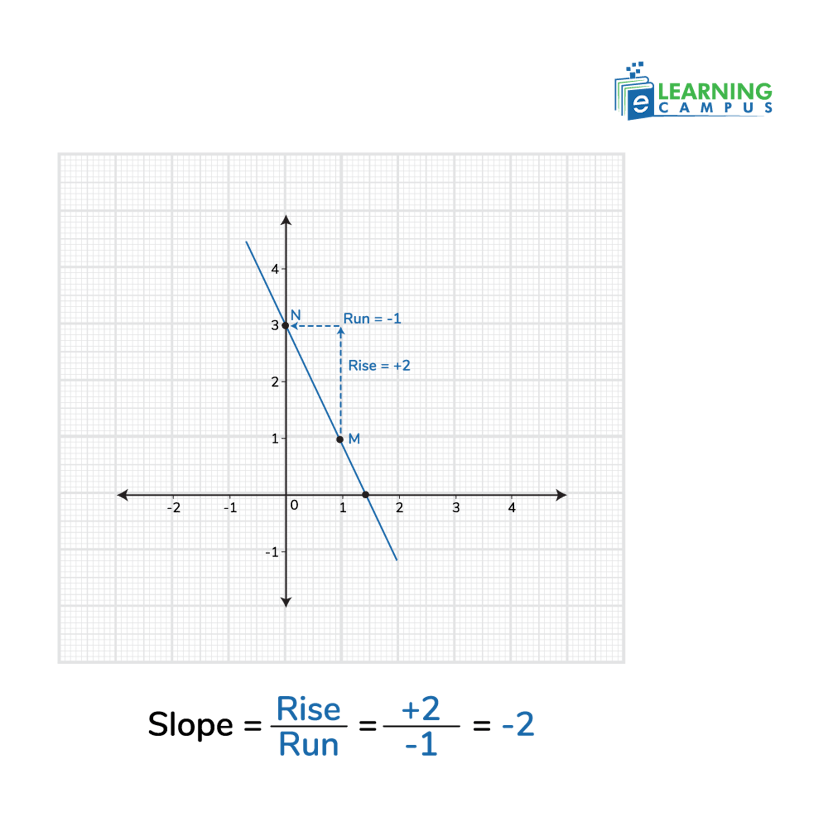
How to Calculate the Slope of a Line on a Graph

To find the slope of a line, we will select two points on the line in the graph.  

We termed them as M and N. 

We have taken M = (1, 1) and N = (0, 3). Draw a right-angled triangle from M to N. We will move up ‘vertically’ to reach N from M. So, the rise = +2. Now we will move left ‘horizontally’ to reach from M to N. The run is -1.

So we found the run and rise. Now, we will use the formula;

slope=riserun\text{slope} = \frac{\text{rise}}{\text{run}}
slope=2−1\text{slope} = \frac{2}{-1}
slope=−2\text{slope} = -2

How to Calculate the Slope of a Line When the Equation Is Given

To find the slope of a line when the equation is given, we have to rearrange it into slope-intercept form (y = mx + b). In this slope-intercept form, ‘m’ is the slope and ‘b’ is the y-intercept. The slope is simply the coefficient of the 'x' term.

Example 

For the equation y = -3x + 4, the slope (m) is -3. 

If the equation is in the standard form Ax + By = C, not in slope-intercept form, then this formula will be used to find the slope.

m=−ABm = -\frac{A}{B}

For example, for the 3x + 2y = 6

A= 3

B= 2 

Putting in the formula

m=−32m = -\frac{3}{2}

So, the slope is -3/2. 

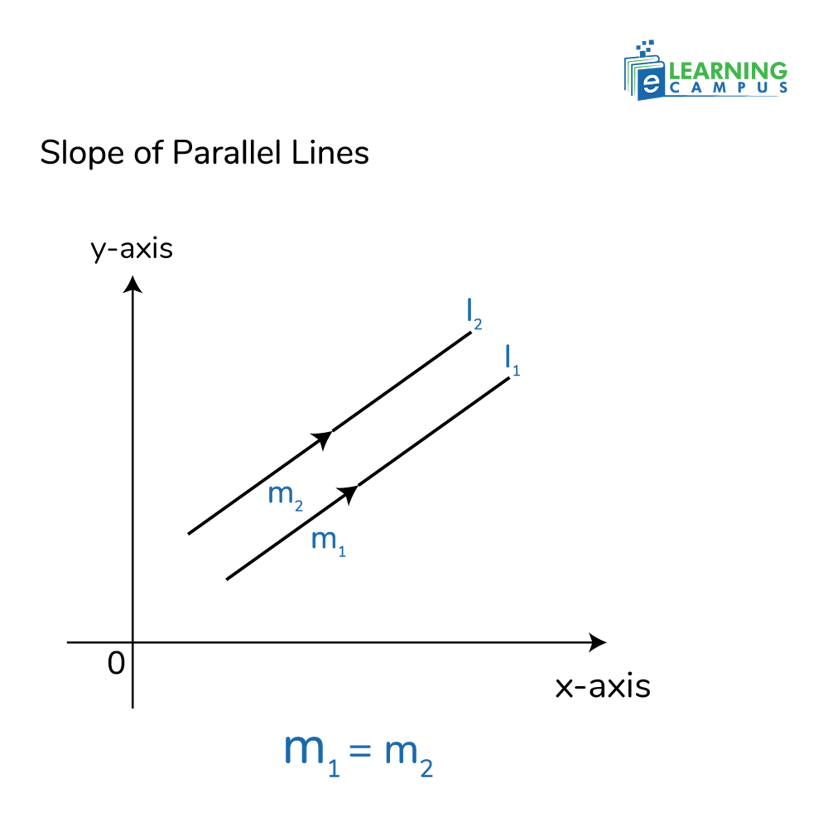
How to Find the Slope of a Parallel Line

To find the slope of a parallel line, we need to determine the slope of the original line, because parallel lines always have the same slope. 

Since parallel lines are equally inclined with the positive x-axis, their angles of inclination are equal. Consequently, the tangents of these angles are also equal. 

Therefore, if the slopes of two parallel lines are represented as m1 and m2, then m1=m2

It means that once we have found the slope of the original line, that is the slope for any line parallel to it. For example, if a line has a slope of 3, any line parallel to it also has a slope of 3. 

How to Find the Slope of a Parallel Line

Methods to Find the Slope of a Parallel Line 

The slope of a parallel line can be calculated using several methods. The methods include calculation from a graph, from an equation in slope-intercept form, from an equation in standard form, and from two points. 

Method 1: From the equation of the line

If the equation of the line is given, the slope can be calculated by putting the values into slope-intercept form. 

Example

Find the slope of a line parallel to

3x+2y=83x + 2y = 8

We will rearrange the equation in slope-intercept form

y=mx+by = mx + b
3x+2y=83x + 2y = 8
2y=−3x+82y = -3x + 8
y=−32x+4y = -\frac{3}{2}x + 4

 In this case, the coefficient of x is 3/2. 

So, the slop is 3/2

It is the slope of the original line. Therefore, the slope of all other lines parallel to the original line will be 3/2

Method 2: From two points on the line

If we are given two points that the original line passes through, we can calculate the slope using the slope formula. 

m=y2−y1x2−x1m = \frac{y_2 - y_1}{x_2 - x_1}

Example

Find the slope of a line parallel to the one that passes through (1,3) and (5,11).

Put the values in the slope of a parallel line formula. 

m=11−35−1m = \frac{11 - 3}{5 - 1}
m=84m = \frac{8}{4}
m=2m = 2

The slope of the original line is 2. Therefore, the slope of all parallel lines will be 2. 

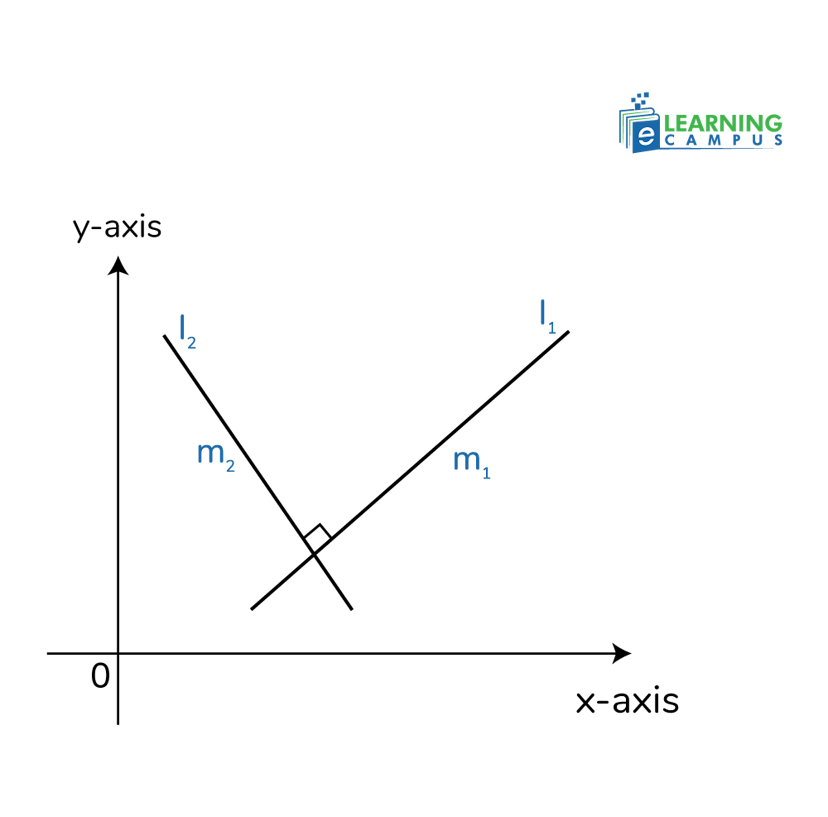
How to Calculate the Slope of a Perpendicular Line

To find the slope of a perpendicular line, we need to find the slope of the original line and take the negative reciprocal of the original line's slope. This means we flip the fraction and change the sign. 

For example, if the original slope is 2/3, the perpendicular slope is -3/2.  

Steps to Calculate the Perpendicular Slope

Find the original slope (m) 

If the line is in slope-intercept form (y = mx + b), the slope is the coefficient 'm'. If the equation is in a different form, rearrange it into y = mx + b to find 'm'. Example: For the line 3x + 2y = 6, solve for y: 

2y=−3x+62y = -3x + 6
y=(−32)x+3y = \left(-\frac{3}{2}\right)x + 3

The original slope (m) is -3/2. 

Find the reciprocal of the slope 

Flip the numerator and denominator of the original slope. The reciprocal of -3/2 is -2/3. 

Make it negative 

Change the sign of the reciprocal to get the negative reciprocal. The negative reciprocal of -2/3 is +2/3. 

How to Calculate the Slope of a Perpendicular Line

How to Calculate the Slope of a Tangent Line

To find the slope of the tangent line to a curve y=f(x) at a given point (x0, y0), we need to find the derivative f′(x) and evaluate it at x=x0​. 

The derivative f′(x0) gives the slope of the tangent line at that point. Below is a clear and concise explanation with steps and examples. The slope of the tangent line formula  is given as; 

Slope of tangent line = f'(a)

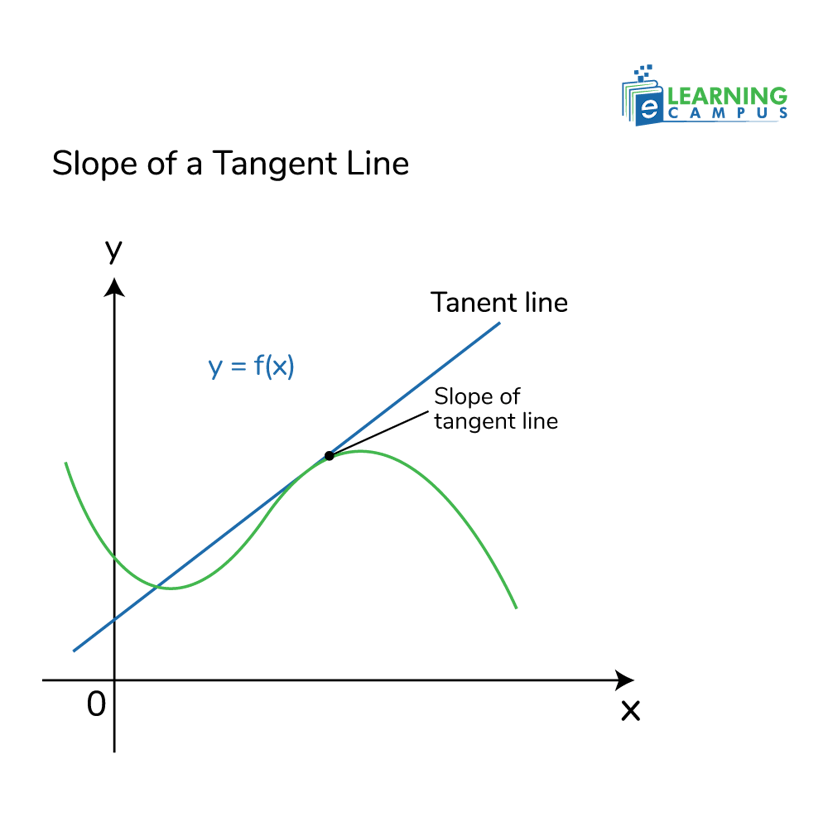
How to Calculate the Slope of a Tangent Line

Steps to Find the Slope of a Tangent Line

Compute the Derivative: Find f′(x), the derivative of the function f(x), which represents the slope of the curve at any point x.

Evaluate at the Given Point: Substitute the x-coordinate of the point (x0​) into f′(x) to get the slope

m=f′(x0)m = f'(x_0)

Example 

Slope of Tangent Line to f(x)=x2 at (1,1)

  • Find the Derivative:
f(x)=x2at(1,1)f(x) = x^2 \quad \text{at} \quad (1, 1)
  • Evaluate at x=1:
f(x)=x2⇒f′(x)=2xf(x) = x^2 \Rightarrow f'(x) = 2x
  • Slope: The slope of the tangent line at (1,1) is
m=2m = 2

Conclusion 

The slope of a line represents its steepness. To calculate it, use the formula m = (y₂ - y₁) / (x₂ - x₁), which represents the change in y-coordinates (rise) divided by the change in x-coordinates (run) between two points on the line. The slope is usually represented by the letter ‘m’. 

Make Math Easy For You 

Are you struggling with learning math and stressed about how to prepare for your exams? We can help you. We have expert online math tutors with years of experience in making math easy for students. You will get personalized and targeted preparation for your exams.

Hire an online math tutor
Hire a tutor now

FAQs