Factors of 12 - What Are They and How to Find Them Easily?

Have you ever wondered why the number 12 appears so often in our daily lives like 12 months in a year or 12 hours on a clock? That’s because 12 is a highly divisible number with many factors that make it unique in mathematics.

In simple terms, factors of 12 are the numbers that can divide 12 evenly without leaving any remainder. Learning the factors of twelve helps students understand multiplication, division and number patterns more effectively.

By the end of this guide, you’ll know all of the factors of 12 and how to find them quickly.

What are the Factors of 12?

In math, factors are numbers that divide another number exactly without leaving any remainder. So, when we talk about the factors of 12, we mean all the numbers that can be multiplied in pairs to make 12.

For Example:

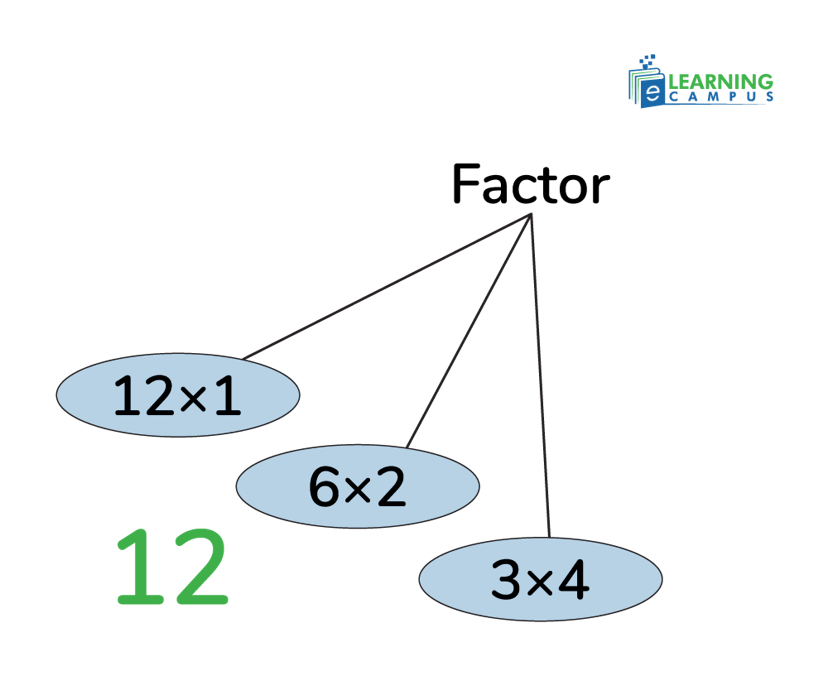
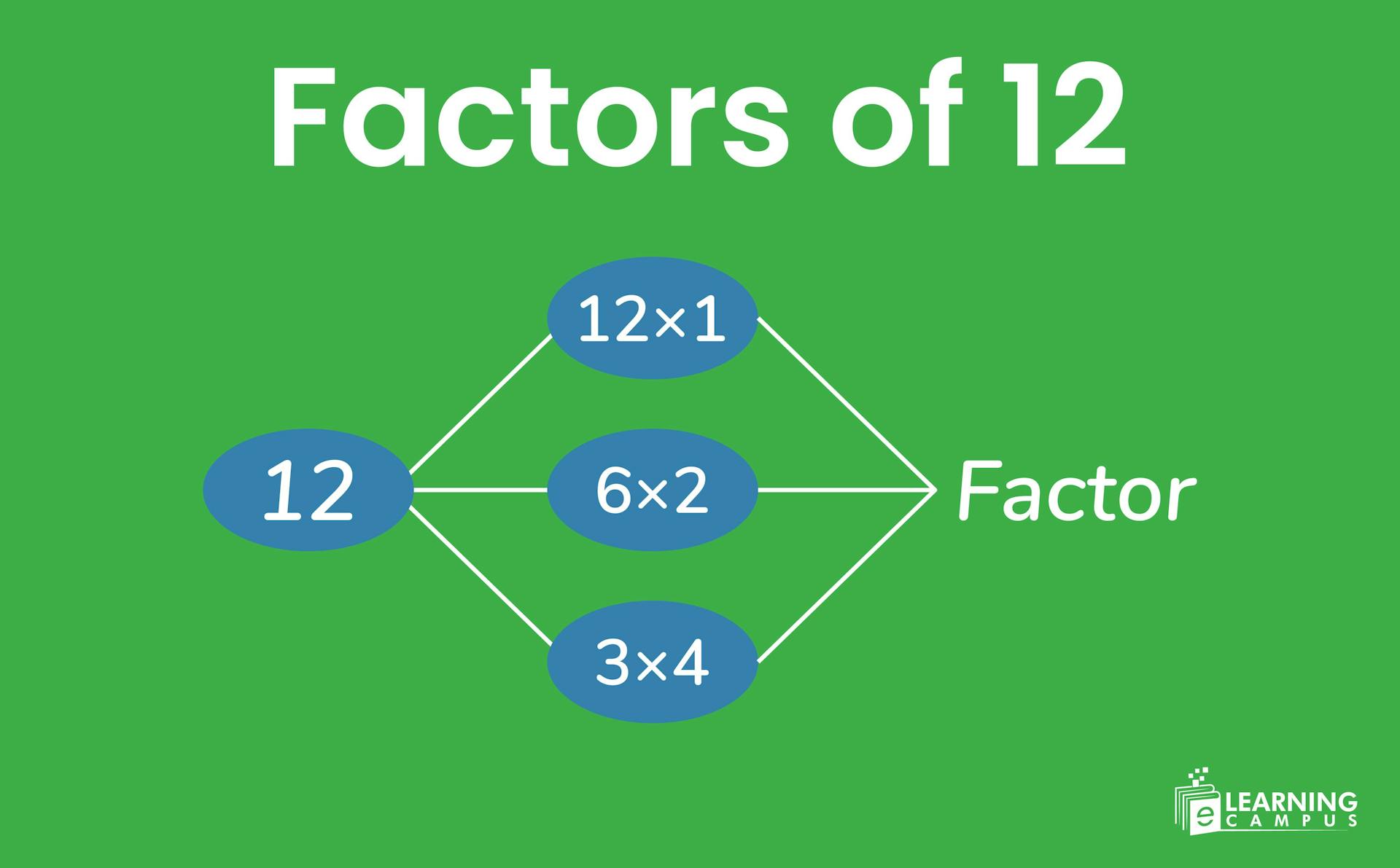
List the Factors of 12

Let’s look at the list of all factors of 12 to understand which numbers divide 12 completely. 

So, the factors of 12 are 1, 2, 3, 4, 6, and 12. These numbers divide 12 completely, with no remainder.

Prime Factors of 12

Prime factors are the smallest numbers that can be multiplied together to make another number.

A prime number is a number that has only two factors: 1 and itself (like 2, 3, 5, 7, 11…).

Example: 

Let’s find the prime factor for 12 step by step:

• Start with the smallest prime number, 2, because 12 is even.

• Divide 6 by 2 again (since it’s still even).

• Now, 3 is also a prime number, so we stop here.
• Now, if we multiply these prime numbers together, we get:

• So, the prime factors of 12 are 2 and 3.

This means 12 is made by multiplying 2 × 2 × 3 - the smallest building blocks that create 12.

Common Factors of 12

Common factors are the numbers that can divide two or more numbers exactly - meaning they are shared factors among those numbers.

Example: 

To find the common factors of 12, 36, and 60, we first list all the factors of each number and then see which ones are the same in all three lists.

Step 1: List the factors of 12, 36 and 60

• Factors of 12: 1, 2, 3, 4, 6, 12
• Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
• Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Step 2: Find the numbers common in all three lists

Step 2: Let’s see which numbers appear in all:

1 appears in all

2   appears in all

3  appears in all

4   appears in all

6 appears in all

12 appears in all

Step 3: Final Answer

The common factors of 12, 36, and 60 are:

1, 2, 3, 4, 6, and 12

Tip for Students: If a number divides all three numbers evenly, it’s a common factor!

Here, 12 is the highest common factor (HCF) of 12, 36, and 60.

Also Read: Difference of Cubes | Formula, Factor & Examples

How to Find Factors of a Number 12

Finding the factors of 12 is very easy if you follow a few simple steps. Let’s go through them one by one.

Example: 

Step 1: Start with 1 and the Number Itself (12)

Every number has 1 and the number itself as its factors.

So, for 12 

The first two factors are 1 and 12 because: 1 × 12 = 12

This is always the starting point when finding factors of any number.

Step 2: Check for Numbers That Divide 12 Evenly

Now, check which numbers divide 12 without leaving any remainder.

12 ÷ 1 = 12 ✓

12 ÷ 2 = 6 ✓

12 ÷ 3 = 4 ✓

12 ÷ 4 = 3 ✓

12 ÷ 5 = 2.4 × (not a whole number)

12 ÷ 6 = 2 ✓

12 ÷ 12 = 1 ✓

All the numbers that divide 12 completely are its factors.

So, the factors of 12 are: 1, 2, 3, 4, 6, and 12.

Step 3: Write Down Factor Pairs of 12

Factors always come in pairs: one small number and one large number that multiply to make 12.

Step 4: Numbers That Multiply to 12 (Factor Pairs)

Let’s write the pairs of numbers that give 12 when multiplied:

1 × 12 = 12

2 × 6 = 12

3 × 4 = 12

So, the factor pairs of 12 are:

(1, 12), (2, 6), and (3, 4).

These pairs show how different numbers work together to make 12.

Step 5: Factors of 12 That Add Up to 12

Now, let’s check which factor pairs also add up to 12:

1 + 12 = 13 × 

2 + 6 = 8 ×

3 + 4 = 7 ×

None of the factor pairs of 12 add up exactly to 12 but they all multiply to make 12.

Step 6: Final Answer

The factors of 12 are 1, 2, 3, 4, 6, and 12, and the factor pairs are (1, 12), (2, 6), and (3, 4).

Factors of Twelve with Examples and Explanation

There are many simple ways to find the factors of 12. Here are three easy methods: multiplication, division and prime factorization explained with examples so students can understand them clearly.

Using Multiplication Method

In this method, we think of all the numbers that can be multiplied together to get 12.

Let’s see all the possible multiplication pairs:

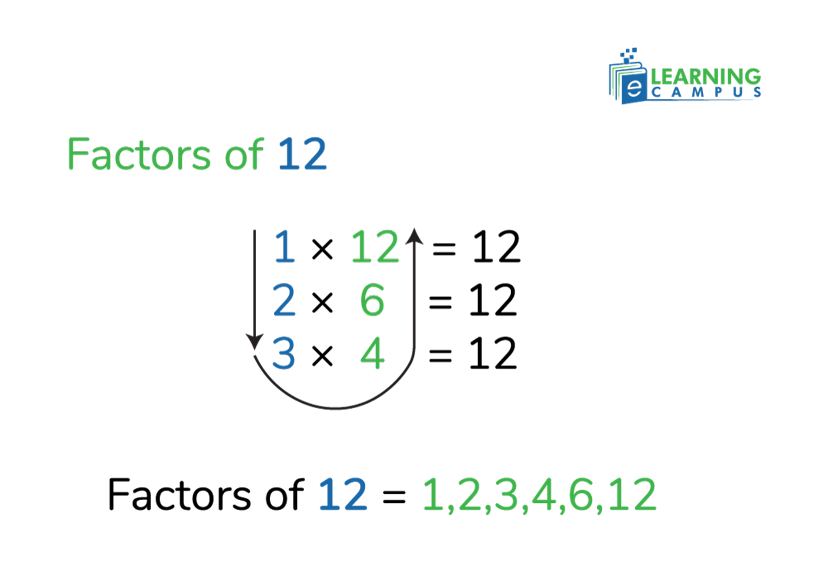
From these pairs, we can see that the numbers 1, 2, 3, 4, 6, and 12 can all multiply to make 12.

So, the factors of 12 are 1, 2, 3, 4, 6, and 12.

Tip: Multiplication pairs are the easiest way for beginners to find factors quickly!

Using Division Method

In the division method, we divide 12 by smaller numbers to see which ones divide evenly (without a remainder).

All the numbers that divide 12 completely are its factors.

So, again, the factors of 12 are 1, 2, 3, 4, 6, and 12.

Tip: If the answer is a whole number, that number is a factor!

Using Prime Factorization Method (12 = 2 × 2 × 3)

The prime factorization method breaks a number down into its smallest prime factors.

Example: 

Step 1: Let’s do it step by step for 12

1. 12 ÷ 2 = 6
2. 6 ÷ 2 = 3
3. 3 ÷ 3 = 1 (stop here because 3 is prime)

Step 2: Now multiply those prime numbers together

12 = 2 × 2 × 3

So, the prime factors of 12 are 2 and 3.

No matter which method you use, the factors of 12 are always 1, 2, 3, 4, 6, and 12, and its prime factors are 2 and 3.

How Factors Help in Fractions, LCM & GCF

Factors are not just for finding which numbers divide another — they also help you simplify fractions, find the Lowest Common Multiple (LCM), and Greatest Common Factor (GCF) in math.

Factors in Fractions (Simplifying Fractions)

When you simplify a fraction, you look for common factors of the numerator (top number) and denominator (bottom number).

Example: Simplify 12/18

Step 1: Write Factors of 12 and 18

• Factors of 12 = 1, 2, 3, 4, 6, 12
• Factors of 18 = 1, 2, 3, 6, 9, 18
• The common factors are 1, 2, 3, and 6
• The greatest common factor (GCF) is 6

Step 2: Now divide both numbers by 6

12 ÷ 6 = 2 and 18 ÷ 6 = 3

Simplified fraction = 2/3

Factors in LCM (Least Common Multiple)

To find the LCM, you look for the smallest number that two or more numbers can divide evenly into.

Example: Find LCM of 12 and 8

• Multiples of 12 = 12, 24, 36, 48, 60
• Multiples of 8 = 8, 16, 24, 32, 40, 48

The first common multiple is 24

LCM = 24

Factors in GCF (Greatest Common Factor)

The GCF is the largest number that divides two numbers exactly — it’s also called the greatest common divisor (GCD).

Example: Find GCF of 12 and 18

Solution: 

• Factors of 12 = 1, 2, 3, 4, 6, 12
• Factors of 18 = 1, 2, 3, 6, 9, 18

The common factors are 1, 2, 3, 6

The greatest one is 6, so GCF = 6

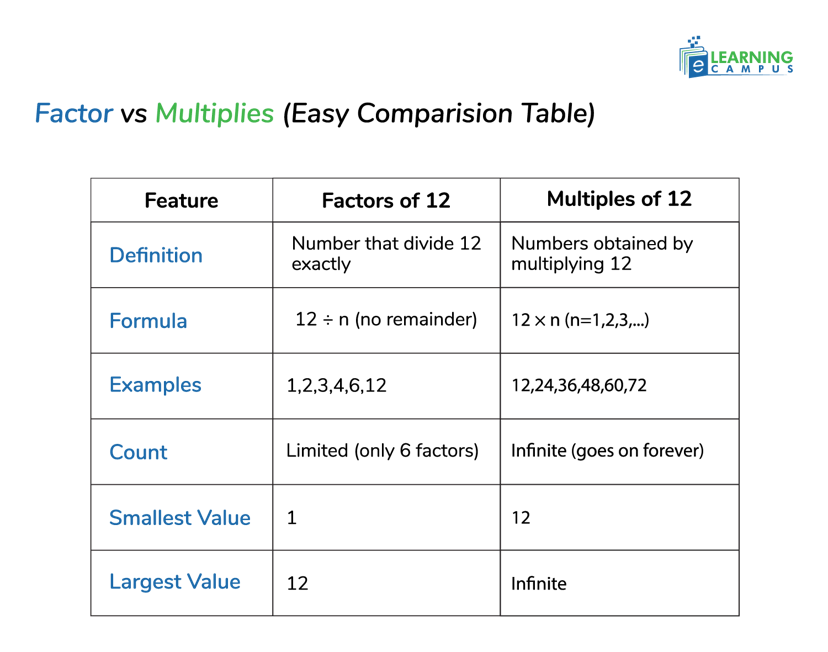
Factors of 12 vs. Multiples of 1

Multiples of 12 are the numbers you get when you multiply 12 by whole numbers like 1, 2, 3, and so on. In simple terms, they are the results of 12 × n (where n = 1, 2, 3, …)

Examples of Multiples of 12:

12 × 1 = 12

12 × 2 = 24

12 × 3 = 36

12 × 4 = 48

12 × 5 = 60

So, the first few multiples of 12 are:

12, 24, 36, 48, 60, 72, 84, 96, 108, 120.

Factors vs Multiples (Easy Comparison Table)

Real-Life Examples Using Factors of 12

1. Arranging Chairs:

If you have 12 chairs and want to arrange them evenly, you can make groups of 2, 3, 4, or 6 chairs - these are the factors of 12.

1. Distributing Items:

If you have 12 candies and want to share them equally, you can divide them among 2, 3, 4, or 6 friends - no candy will be left!

1. Time Calculation:

There are 12 hours on a clock face. Factors of 12 (like 3, 4, and 6) help divide the clock into equal parts such as quarter hours (3 hours) or half (6 hours).

Practice Zone - Find Factors of Other Numbers

Test your skills by finding factors of other numbers like 6, 8, or 24. Use the same steps you learned for factors of 12. Start from 1 and find all numbers that divide evenly!

How to Find Factors of Any Number (Simple Trick)

To find factors of any number, start with 1 and the number itself. Then, check which numbers divide it without leaving a remainder.

Example: For 10 → 1, 2, 5, and 10 are its factors because 10 ÷ 2 = 5 exactly.

Factors of 6, 8, and 24 (Related Numbers to 12)

Let’s look at some numbers closely related to 12:

• Factors of 6: 1, 2, 3, 6
• Factors of 8: 1, 2, 4, 8
• Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24