Relationship Between Electricity and Magnetism

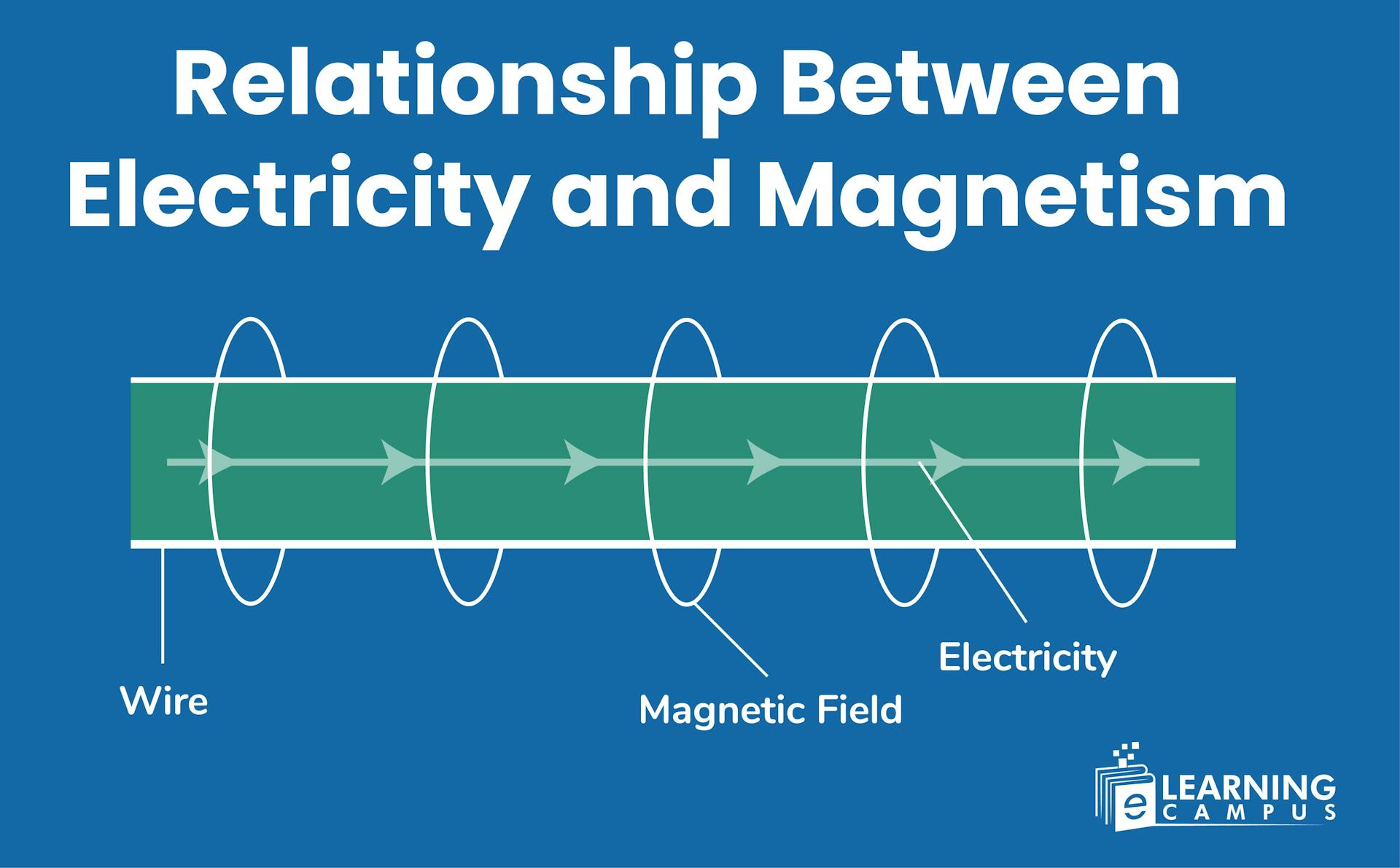
Electricity and magnetism are two interlinked forces found in nature. Electricity is the movement of charged particles, and the force exerted by these moving charges is called magnetism. Combined, they are known as electromagnetism.

Moving electric charges generate magnetic fields, and changing magnetic fields can induce electric currents.

In this blog, you will learn about electricity and magnetism and their relationship. 

What is Electricity 

Electricity is the movement of electric charges through a conductor. The flow of charges induces an electric current.

How Electricity is Generated 

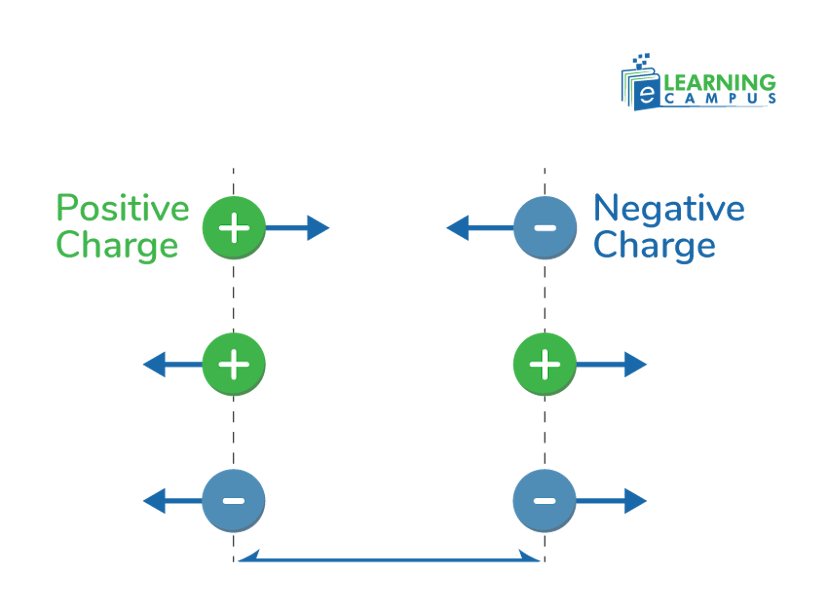
Electricity is generated when electrons move from one point to another due to a potential difference. An atom is the fundamental particle of matter. It consists of three particles, namely the electron, proton, and neutron. Electrons have a negative charge, protons have a positive charge, and neutrons are neutral. 

According to Columb’s law, there is a force between these charged particles known as the electrostatic force. Particles that contain the same charge repel each other, and particles with opposite charge attract each other. The force of repulsion or attraction depends on how close the charges are to each other. 

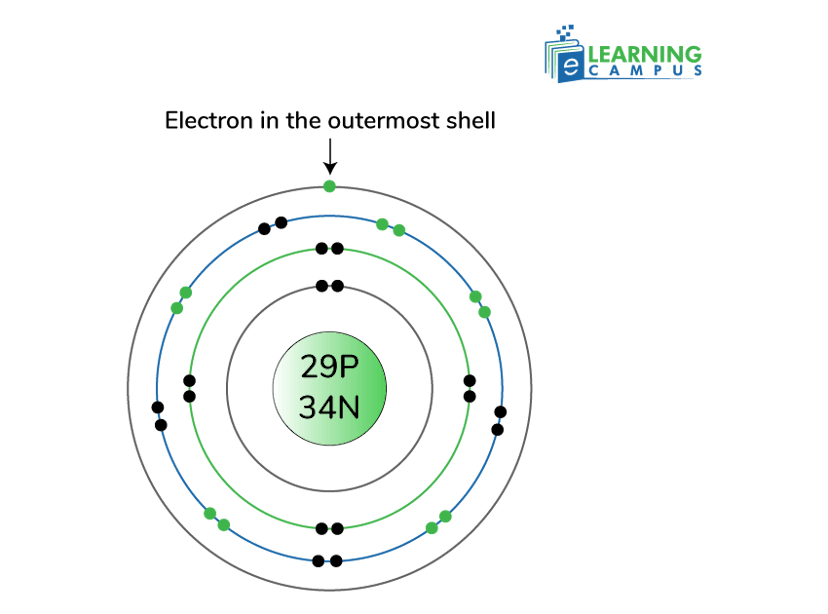
If an electron is freed from an atom, it will move and generate electricity. For example, copper has 29 electrons, and the outermost shell has one free electron. With the electrostatic force, the free electron can be ejected from orbit, allowing it to move freely between orbits. 

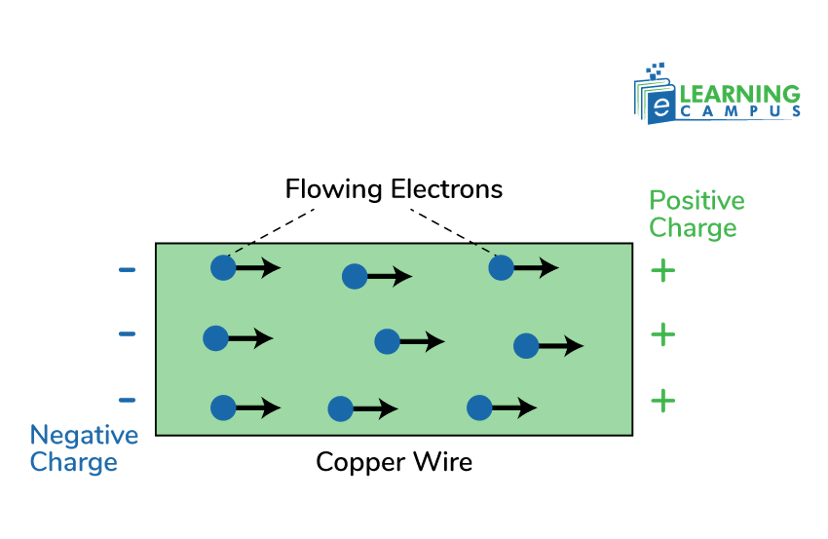
Now this free electron will be attracted by the proton of another shell, resulting in the ejection of the electron from that shell. This process continues and creates a flow of electrons known as an electric current. 

Types of Electricity 

Electricity is categorized into two main types, i.e, static electricity and current electricity. This categorization is based on the flow of electric charge. 

Static Electricity

Static electricity occurs when there is an imbalance of electrical charges on the surface of an object. It is usually generated by friction, like rubbing a balloon on your hair. It transfers electrons and creates a charge imbalance.

Current Electricity

Current electricity is generated by a continuous and regular flow of charge in a conductor. 

Key Terms and Units of Electricity

• Voltage (V): Voltage is the electrical potential difference between two points. It is the force or pressure that pushes the electrical charge through a circuit. It is measured in volts.
• Current (A): Current is the rate at which electrical charge flows through a conductor. It is measured in amperes (amps).
• Resistance (Ω): Resistance is the opposition to the flow of current. The unit of measurement of resistance is ohms (Ω).
• Power (W): Power is the rate at which electrical energy is used or transferred. It is measured in watts (W). 

What is magnetism 

Magnetism is a force caused by moving electric charges. It results from the motion of electrons within atoms. It is actually a force that causes materials to attract or repel each other. It can exist naturally, such as in magnets, or can be induced by electric currents.

Magnetic Field 

A magnetic field is an area around a magnet or an electric current in which the influence of magnetic force can be detected. These are visible to human eyes. The movement of electric charges produces magnetic fields. An electric current that flows through a wire creates a magnetic field around it.

The strength of the magnetic field depends on the amount of current that flows through a wire. 

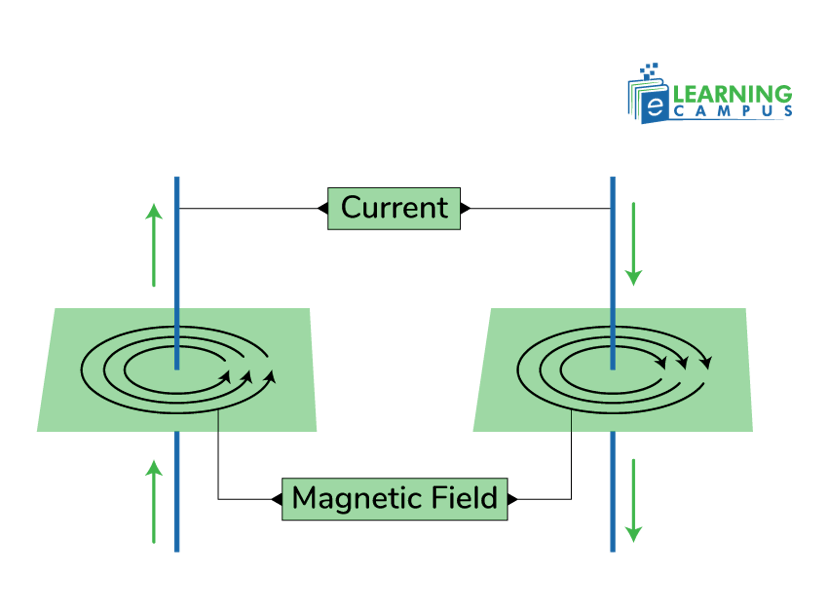
Ampere’s Law and Relation Between Current and Magnetic Field 

Ampere's law describes the relationship between a magnetic field and the electric current that produces it. This law states that ‘the line integral of the magnetic field around a closed loop is proportional to the total electric current passing through it.’

Mathematically, it is represented as

In which,

So, Ampere’s law describes that the strength of the magnetic field depends on the amount of current passing through a wire. The magnetic field will be strong if more current passes through a wire. Less current will cause a weak magnetic field. 

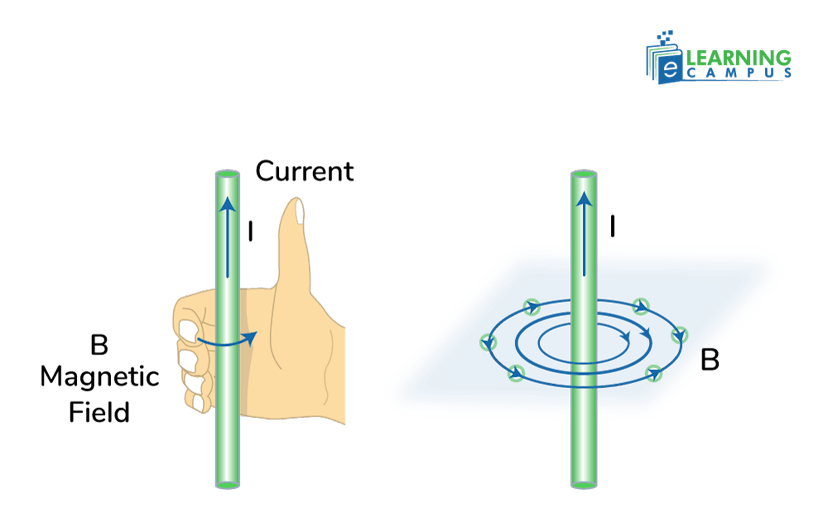
How to Determine the Direction of Magnetic Field and Current 

The direction of a magnetic field and current in a wire can be determined using the right-hand rule. For a straight wire that contains current, point your right thumb in the direction of the current. Your fingers will curl in the direction of the magnetic field lines.  

Eletromagnetism 

The relationship between electricity and magnetism is called electromagnetism. It describes how electric charges and magnetic fields interact, and how moving electric charges (current) can create magnetic fields. It also describes how changing magnetic fields can induce electric currents.

Maxwell’s Equations and Electromagnetism

Maxwell's equations are a set of four differential equations that form the foundation of electromagnetism. They describe the interaction of electric and magnetic fields. They explain how electric and magnetic fields are generated and altered by electric charges and currents. 

Maxwell’s First Equation 

Maxwell's first equation describes the relationship between electric fields and electric charges. It is also known as Gauss’s law of electricity. This equation states ‘that the electric flux density (electric field passing through a given surface) through any closed surface is proportional to the total electric charge enclosed by that surface.’

Maxwell’s first equation is given as

▽. Edv=ρv

In which, 

• ∇ ⋅ is the divergence operator.
• E is the electric field vector.
• D is the electric displacement field.
• ρ is the electric charge density

Derivation of Maxwell’s First Equation 

We can derive Maxwell’s first equation with the help of Gauss’s law. Gaussse’s law is represented as;

∯ E.ds = Qenclosed………(i)

As the system consists of many surfaces, but the volume remains the same. So, we will convert the surface integral to a volume integral through the divergence of the same vector. So, it will be written as;

∯ E.ds = ∭ ▽. Edv……….(ii)

Combining equations (i) and (ii)

∭▽. Edv =Qenclosed …….. (iii)

If some amount of charge is supplied to a system, it will spread over its volume. 

So, the volume charge density will be represented as;

pv=dvdQ​

dQ=pvdv

The integration of the equation gives

Q=∭ρvdv……. (iv)

By substituting equation (iv) in equation (iii)

∭▽. Edv = ∭ρvdv

▽. Edv = ρvdv

Thus, Maxwell's first equation is proved. It is also known as Gauss’s law of electrostatics. It is represented as;

▽. Edv = ρvdv

Maxwell’s Second Equation

Maxwell's second equation states ‘that the Magnetic field lines always form closed loops. They have no beginning or end.’ It is also known as Gauss's law for magnetism. It describes that the magnetic flux through any closed surface is always zero.

Mathematically, it is represented as;

▽. B = 0 

Where,

• B is the magnetic field. 
• ∇ ⋅ is the divergence operator.

Derivation 

It is based on Gauss’s law of magnetostatics. It is represented as;

∯ B . ds = ϕenclosed….. (i)

As we know, the magnetic flux in an enclosed surface is zero.

∯ B . ds = 0……(ii)

Converting surface integral into volume integral through divergence of the same vector.

∯ B . ds = ∭ Δ . Bdv …….(iii)

Substituting equation (iii) in (ii)

∭ Δ . Bdv = 0

This equation can only be satisfied by two conditions. Either volume (v) should be zero, or magnetic field (B) should be zero. 

The volume of any surface can never be zero. So the magnetic field should be zero. Thus, 

Δ . B = 0

Hence, we proved Maxwell’s second equation. This equation shows that the magnetic flux through any closed surface is always zero. 

Maxwell’s Third Equation 

Maxwell's third equation explains the induction of an electric field by changing magnetic field. It is based on Faraday’s law of electromagnetism. It states ‘that the electromotive force (EMF) around a closed loop is equal to the negative rate of change of magnetic flux through the loop.’

Mathematically, it is represented as;

▽×E=−δBδt​

Derivation 

Maxwell’s third equation is based on Faraday’s Law.

emfalt​=−dϕdt​…….(i)

The magnetic flux on an arbitrary surface ‘S’ is,

ϕ = ∬ B.ds

Substituting the value of ϕ in equation (i)

emfalt​=−∬ B.dsdt

emfalt​=∬−(δBdt​).ds…….. (ii)

Since the coil is a closed path, the induced alternative emf can be written as a closed integral,

emfalt = ∮ E . dl……..(iii)

Combining equations (ii) and (iii)

∮ E . dl =∬−(δBdt​).ds……(iv)

According to Stokes’ theorem, contour integration (integrating a function along a curve) can be converted to surface integration. So,

∮ E . dl = ∬ (▽× E ) .ds

Substituting the value in equation (iv)

∬ ( ▽× E ) ds =∬−(δBdt​).ds

▽× E =−(δBdt​)

Thus, we derived Maxwell’s third equation.

Maxwell’s Fourth Law

Maxwell's fourth equation explains the generation of magnetic field by a change in the electric field. It is also known as the Ampere-Maxwell equation. 

Mathematically, it is written as;

▽×H=J+(∂D∂t​)

Derivation 

It is based on Ampere's circuital law.

∮ B.dl = μ0i…….(i)

Using Stokes’ theorem

∮ B.dl = ∮S ( ∇ × B ).ds…..(ii)

Combining equations (i) and (ii)

∮s( ∇ × B ).ds = μ0i …..(iii)

i = ∮s J . ds…..(iv)

Combining equations (iii) and (iv)

∮s ( ∇ × B ) .ds = μ0 ∮s(J . ds )

∮s ( ∇ × B ) .ds - μ0 ∮s (J . ds ) = 0

∮s [ ( ∇ × B ) - μ0 J ] .ds = 0

( ∇ × B ) − μ0 J = 0

( ∇ × B ) = μ0 J

Here, B = μ0 H

Hence, ∇ × H = J….. (v)

On the modification of this equation, we can get our required derivation. It can be achieved by using modified Ampere’s law.

∮ B . dl = μ0 i + id

Where, id is the displacement current. So, equation (v) will become

∇ × H = J + Jd…..(vi)

Here, jd is the displacement current density, and its value is 

Jd = ϵ0 (∂E∂t)

ϵ0E=D

Jd =(∂D∂t)

By substituting the value in equation (v)

∇ × H = J +(∂D∂t)

Thus, we derived Maxwell’s fourth equation.

Conclusion

Electricity and magnetism are two closely related phenomena of force. Combinely, they are known as electromagnetism, a fundamental force in physics. Electricity involves the presence and flow of electric charge, and magnetism is a force exerted by moving electric charges, particularly through magnetic fields.