Convert Radians to Degrees

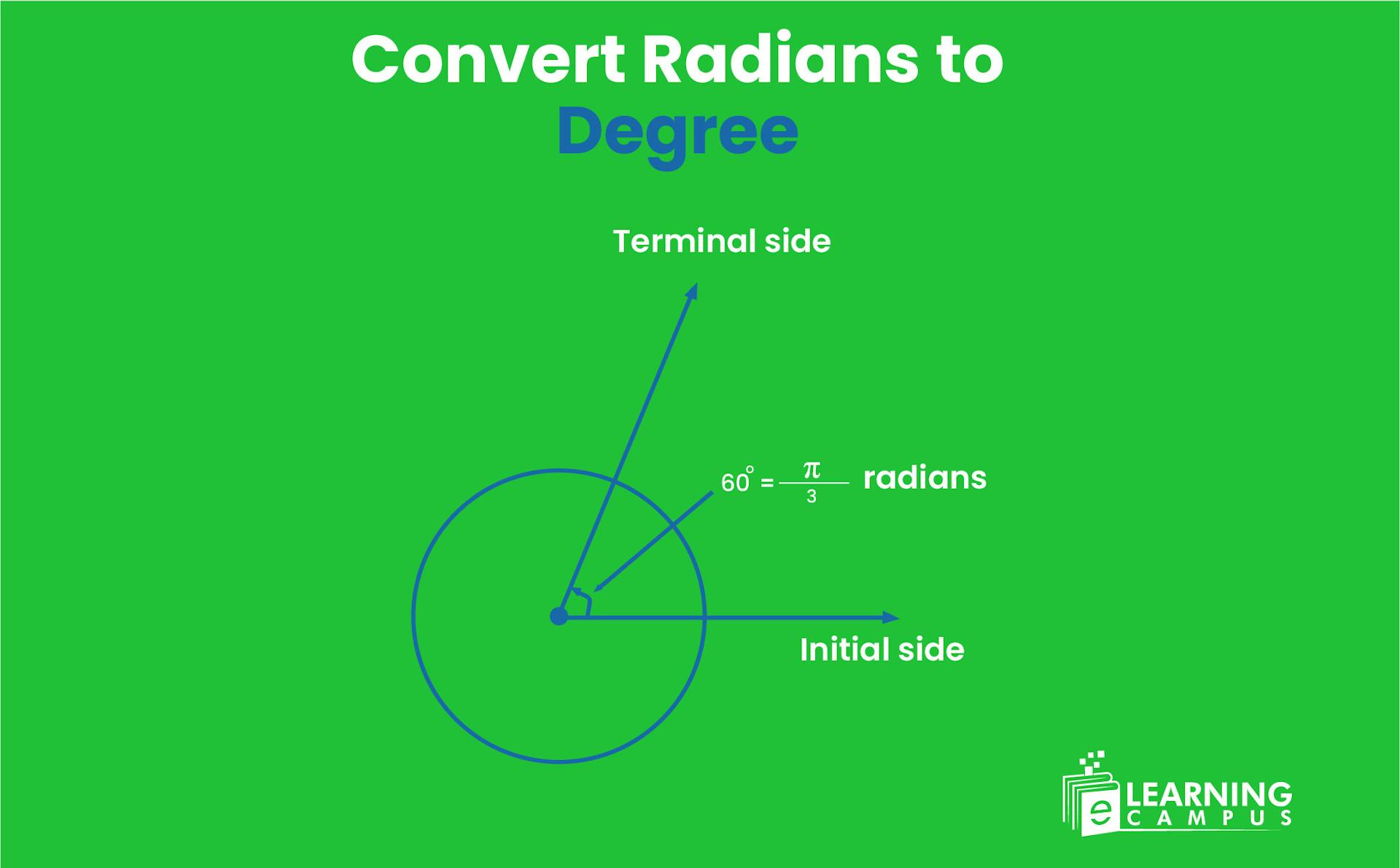
From sketching to drawing and building skyscraper buildings, the measurement of angles plays an important role. Angles can be measured in two units: radians and degrees. Understanding how to convert radians to degrees is essential for students, engineers, mathematicians, and anyone working with angles.

In this blog, you will learn about the units of angle, the difference between radian and degree, and how to change a radian to a degree in simple steps. 

Difference Between Radian and Degree

Radian and degrees are both units of measurement of angles. The difference between radian and degree lies in their definition and the way they relate to a circle. Let’s understand it in detail. 

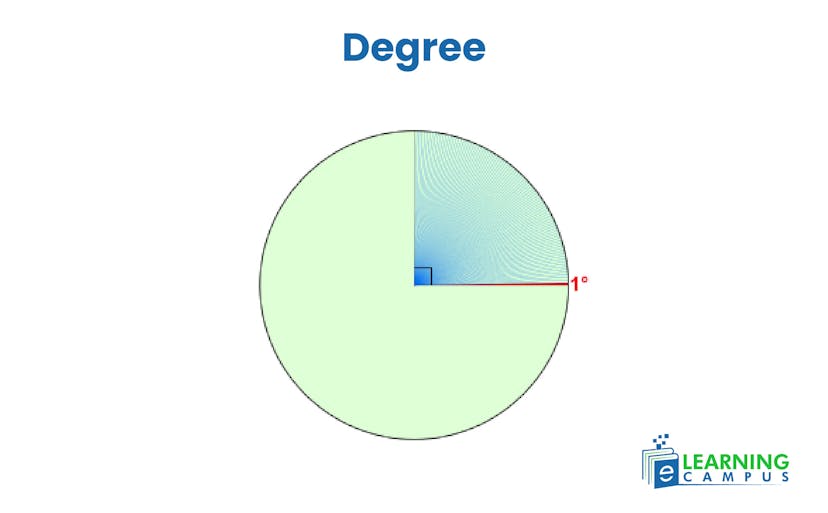
Degree 

Degree is the unit of measurement of angles. It is an angle made by a unit (one) part at the center of the circle having 360 equally divided parts. It is denoted by '°'. 

In the below diagram, 1 degree is shown in red.

Radian 

A radian is an angle made by an arc at the center of a circle that is equal to the radius of the circle. It is an international unit of measurement of angles. A radian can also be defined as the angle measurement unit using a circle's radius. 

An angle formed by an arc that equals the radius of the circle is defined as one radian. When the radius revolves 180 degrees, it makes a π radian. When the radius revolves 360 degrees, it makes 2π radians. 

Relationship Between Radians and Degrees 

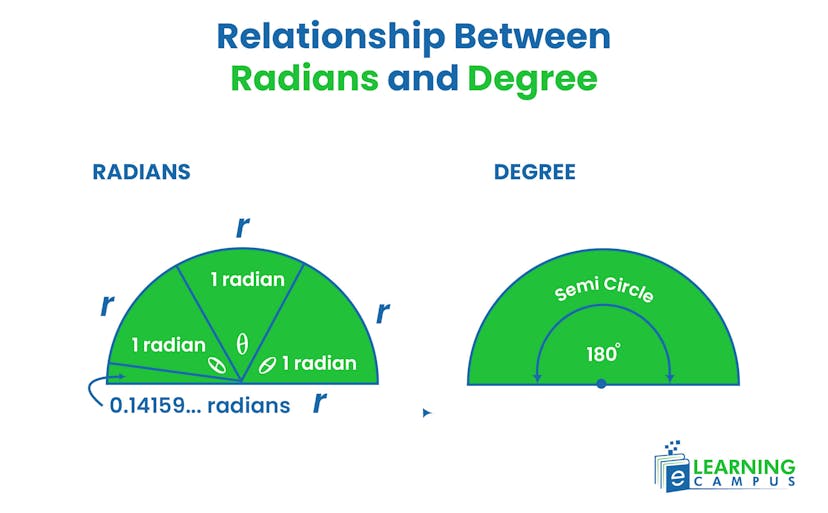
The relationship between radians and degrees can be understood by considering a circle. 

Let’s consider two semicircles as given below. 

A semicircle has 180 degrees. 

Considering the first circle, if we wrap the radius of the circle ‘r’around its circumference (that is one radian), we will require three and 0.141 radians to complete the semicircle. 

So, 3 radians +0.141 radian =3.141 radians=π radians

As 3.141=π

It means a semicircle is equal to π radians. Also, a semicircle is equal to 180 degrees;

• 180 degrees = π radians

A full circle will have 2π radians and 360 degrees.

• 360 degrees = 2π radians 
• 1 radian = 180°/π (approximately 57.296°) 
• 1 degree = π/180 radians (approximately 0.01745 radians) 

The Formula to Convert Radians to Degrees

An angle can easily be converted from radians to degrees with the help of a formula. The formula to convert radians to degrees is given by;

How to Change a Radian to a Degree– Steps

Let’s learn about the steps on how to change a radian to a degree. With these steps, you can easily change radians to degrees. 

• Identify the angles in radians.
• Start with the angle you want to convert. 
• Multiply the radians with degree and divide by pi π. 
• Round off the number. 

Examples of Radians to Degrees Conversion

We will look into the examples of radians to degrees conversion to understand it better. 

Example 1:

Convert 2 radians to degrees. 

We will use the formula to convert 2 radians in degrees.

Substitute the radians with 2.

So, 2 radians is equal to 114.64 degrees. 

Example 2:

Convert 2pi radians to degrees. 

To convert 2 π radians to degrees, we will use the same formula. 

Eliminate the pi

So, radian 2 pi is equal to 360

Example 3: 

Convert 5 radians to degrees.

Let’s follow the formula and procedure.

So, 5 radians in degrees is equal to 286.62.

Example 4:

Change 20 rad to degree.

So, 20 radian is equal to 1146.4 degrees.