Concentric Circles

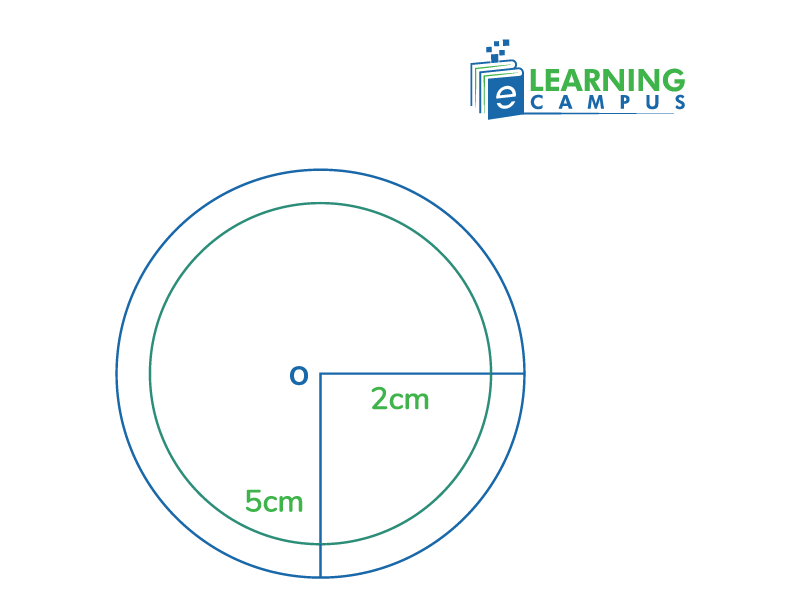
Two or more circles with the same center point but different radii are known as concentric circles. They are designed in a series of circles nested inside each other, sharing the same central point. The region between two concentric circles is called an annulus.

In this blog, you will learn about concentric figures and circles, their formula, equations, and the theorem. 

What are Concentric Circles

In geometry, concentric describes figures, such as circles or spheres, that share the same center point. Concentric figures have different sizes (radii) but are positioned around a common central point. 

Coplanar circles that have a common center are called concentric circles. In Euclidean geometry, these are two or more circles that share the same center point but have different radii. 

Annulus

An annulus is the region between two concentric circles. It resembles a ring. It is formed by the area between the outer and inner edges of these circles.

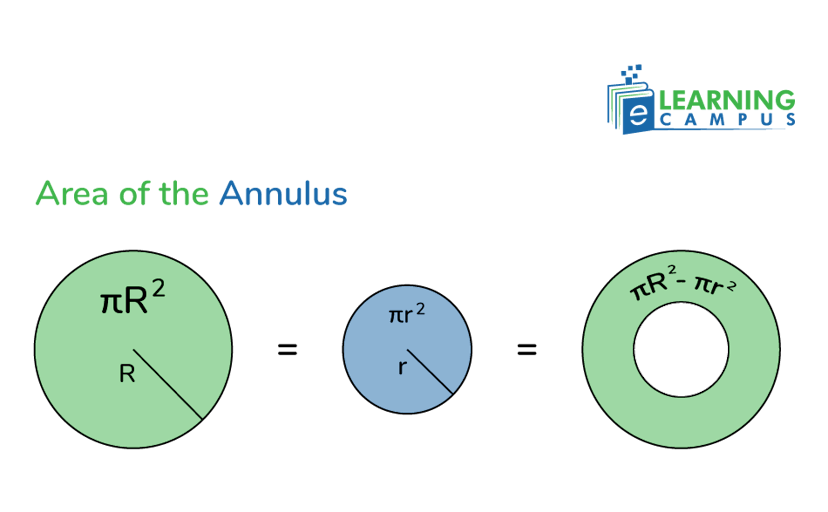
The area of an annulus can be calculated by subtracting the area of the inner circle from the area of the outer circle.

The area of the outer circle is given as;

And the area of the inner circle is given as;

So, the general formula to find the area between two concentric circles will be;

Where,

•  ‘R’ is the radius of the outer circle.
• ‘r’ is the radius of the inner circle. 

Concentric Circle Theorem

The Concentric Circles theorem states that 

“If a chord of the larger of two circles is tangent to the smaller circle, then the point of tangency bisects the chord”. 

Let’s explain it.

Consider we have two circles with the same center. If a line segment (chord) of the outer circle touches the smaller circle and also cuts through the larger circle, then the point where it touches the smaller circle will be exactly halfway along the length of the line segment. 

Proof of the Concentric Circle Theorem

We will prove the theorem of cencentric circles with the help of an example and a diagram.  

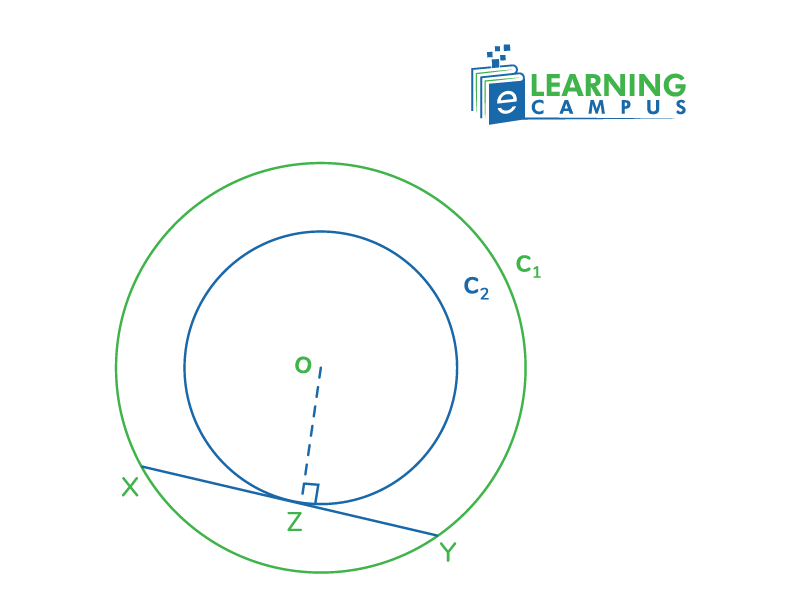
Suppose we have two circles that are concentric, i.e., C1 and C2 with a common center O. The chord XY of the outer circle C1 touches the inner circle C2 at the point Z. As shown in the figure below.  

According to the theorem, the distance from XZ should be equal to YZ. 

To prove, XZ=YZ

As XY is the chord of the outer circle, it is also tangent to the inner circle that touches at the point Z. 

OZ is the radius of the inner circle, C2.

We know that the radius is always perpendicular to the tangent.

So, OZ ⊥ XY

Now XY is a chord of the inner circle and OZ ⊥ XY. 

It means that OZ bisects XY. 

A perpendicular from the center of a circle always bisects the chord. Therefore, OZ bisects XY into two equal segments. 

Thus, XZ=YZ  

Hence, we proved the concentric circle theorem. 

Conclusion 

Concentric circles are geometric figures consisting of two or more circles that share the same center point but have different radii. It means they are all centered around the same middle point, but vary in size, with some circles nested inside others.