elearning BlogComparing Fractions 

Comparing Fractions 

Comparing Fractions

Comparing fractions is a process of comparing two or more fractions. It determines which fraction is larger and which is smaller. To compare fractions, we either need to convert them to equivalent fractions or use cross-multiplication to compare the fractions directly. 

How to Compare Fractions

There are several ways to compare fractions. It follows certain sets of rules related to the numerators and denominators that make comparison easy. The two common methods for fraction comparison are the decimal method and the same denominator method. 

We will learn different methods of fraction comparison in detail.

Decimal Method of Comparing Fractions   

In the decimal method of comparing fractions, we convert fractions into their decimal equivalents and then compare the decimal values. The fraction with the larger decimal value is considered the larger fraction.

Example  

Which one of the following fractions is bigger?

36or512\frac{3}{6} \quad \text{or} \quad \frac{5}{12}

First, we will convert the fraction into a decimal value by dividing the numbers. 

36=0.5\frac{3}{6} = 0.5
512=0.416…\frac{5}{12} = 0.416\ldots

Now, compare the decimal value. 

0.5 is greater than 0.416.

So, the fraction  3/6 is greater than

512\frac{5}{12}

It can also be expressed as

36>512.\quad \frac{3}{6} > \frac{5}{12}.

Comparing Fractions With Same Denominator

One of the methods of fraction comparison is comparing fractions with same denominator. To compare fractions with like denominators, we just look at the numerators of the fractions. The fraction with the greater numerator is greater.

Example  

Consider two fractions 35and15.\text{Consider two fractions } \frac{3}{5} \quad \text{and} \quad \frac{1}{5}.
To find which fraction is greater, we will look at the numerators.\text{To find which fraction is greater, we will look at the numerators.}
3>1,so35>15.3 > 1, \quad \text{so} \quad \frac{3}{5} > \frac{1}{5}.
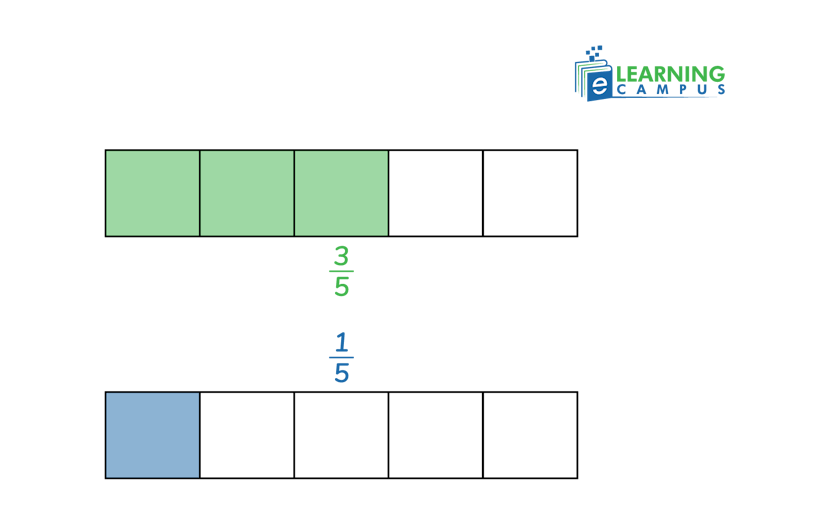
comparing fractions with same denominator

Compare Fractions With Unlike Denominators

To compare fractions with unlike denominators, we first need to make the denominators the same. Once the denominators become the same, it becomes easy to compare them. 

Let’s look at the example.  

Compare

13and35\frac{1}{3} and \frac{3}{5}
  • Observe the denominators. They are different. So, we will make them the same by finding LCM (the lowest common multiple). 

 LCM(3, 5) = 15

  • Now multiply the 1st fraction by 55, that is, 
13×55=515\frac{1}{3} \times \frac{5}{5} = \frac{5}{15}
  • Also, multiply the second fraction fraction with 33.
35×33=915\frac{3}{5} \times \frac{3}{3} = \frac{9}{15}
  • Now compare the fractions
515and915\frac{5}{15} \quad \text{and} \quad \frac{9}{15}
  • The fraction with a larger numerator is bigger.
915>515,so35>13\frac{9}{15} > \frac{5}{15}, \quad \text{so} \quad \frac{3}{5} > \frac{1}{3}

Compare Fractions With the Same Numerator

We can compare fractions with the same numerators. In this method, we observe the numerators of fractions and and then compare. 

The fraction with the smaller denominator is larger, and the fraction with the larger denominator is smaller. 

Example  

Compare

36>38\frac{3}{6} > \frac{3}{8}

Observe the denominators. 

The denominator 38 of is larger than 36. 

36>38,so36 is bigger than 38.\frac{3}{6} > \frac{3}{8}, \quad \text{so} \quad \frac{3}{6} \text{ is bigger than } \frac{3}{8}.
36>38\frac{3}{6} > \frac{3}{8}

Comparing Fractions With Cross Multiplication 

Cross multiplication is another way to compare fractions. In cross multiply to compare fractions, we simply multiply the numerator of one fraction by the denominator of another fraction. 

We will understand it with the help of an example.  

Example 

Compare

38<25\frac{3}{8} < \frac{2}{5}

Multiply the numerator of the first fraction by the numerator of the second fraction.

3×3=153 \times 3 = 15
2×8=162 \times 8 = 16

Therefore, ⅖  is greater than ⅜. 

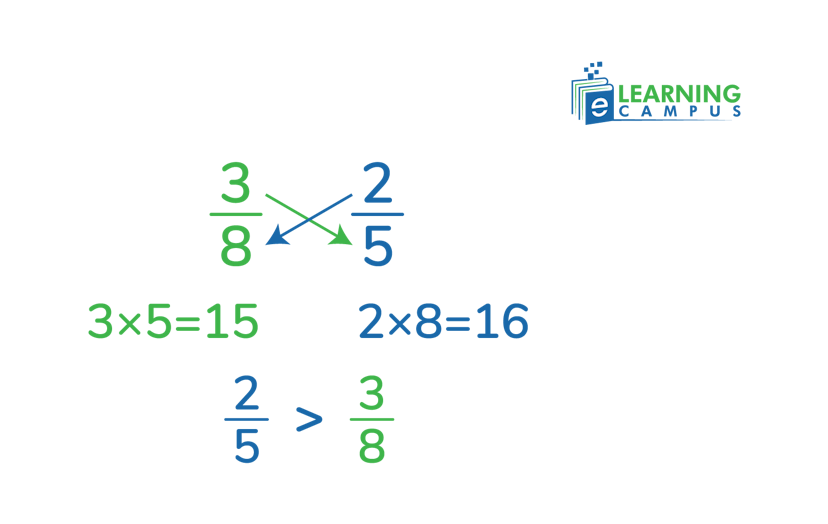
cross multiplication to compare fractions

Compare Fractions on a Number Line

A number line helps visualize the fraction. We can easily compare fractions on a number line. On the number line, the fractions increase from left to right. It means that the fraction on the left side of the number line will be smaller than that on the right side. 

Example 

24=0.5,34=0.75,44=1\frac{2}{4} = 0.5, \quad \frac{3}{4} = 0.75, \quad \frac{4}{4} = 1
On the number line:\text{On the number line:}
0—24—34—440 \quad \text{---} \quad \frac{2}{4} \quad \text{---} \quad \frac{3}{4} \quad \text{---} \quad \frac{4}{4}

To compare the fractions of a number line, we will first plot them on the number line. As shown in the figure below. 

From the given figure, we can evaluate that 2/4 is smaller than ¾ and ¾ is smaller than 4/4. 

24<34<44\frac{2}{4} < \frac{3}{4} < \frac{4}{4}
Compare Fractions on a Number Line

Compare Fractions Worksheet

Worksheets are essential tools to learn and understand the comparison of fractions. We provide you with the compare fractions worksheet PDF to fortify your foundation. Download and practice the worksheet to enhance your problem-solving skills. 

Download PDF

Comparing fractions helps us to determine if one fraction is greater than, less than, or equal to another. We used several easy methods of comparing fractions to help students understand it easily. 

Learn Math With Expert Tutors 

Are you looking for expert online math tutors to learn math in easy steps? We are at your service. We have expert math teachers to make your kids champions of math. You will get one-on-one online math classes at your schedule.

Online math tutor
Hire a Tutor Now

FAQs